
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические и гиперболические функции
Тригонометрические фу́нкции — математические функции от угла
Тригонометрические и гиперболические функции в пространстве Y В плоскости комплексного переменного z тригонометрические функции определяются через функции sin(z), cos(z), которые выражены формулами
Гиперболические функции выражаются через тригонометрические
Особенность этих формул заключается в том, что они представляют функции от двух комплексных переменных z,
Алгебраические многочлены. Теорема Безу. Основная теорема алгебры- теорема Гаусса Алгебраическим многочленом степени и называется сумма целых неотрицательных степеней переменной х, взятых с некоторыми числовыми коэффициентами, т. е. выражение вида
Для сокращенной записи многочленов употребляют обозначения Два многочлена Только в том случае, когда равны их коэффициенты при одинаковых степенях х. Теорема 8.1. Для любых двух многочленов
Причем степень И Многочлен Остатком от этого деления. Замечание. Формулу (8.1) можно записать так:
Если остаток от деления Многочлен Когда существует многочлен
Многочлен
Два многочлена называются взаимно простыми, если они не имеют других общих делителей, кроме многочленов нулевой степени (т. е. постоянных). Наибольшим общим делителем отличных от нуля многочленов Литель этих многочленов. Наибольший общий делитель многочленов
Наибольший общий делитель многочленов Мощью алгоритма Евклида. Если (8.2) То Замечание. Наибольший общий делитель многочленов определен с точностью до постоянного множителя: если Нуля, также является их наибольшим общим делителем Формулировка теоремы Безу Теорема Остаток от деления многочлена Следствия из теоремы Безу 1. Число Отсюда, в частности, следует, что множество корней многочлена 2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми). 3. Пусть Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на единицу меньше: если
Таким образом, один корень найден и далее находятся уже корни многочлена Основная теорема алгебры. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Следствие 1. Любой многочлен
где
Следствие 2. Если многочлены
В самом деле, по условию многочлен
Это следствие позволяет рассматривать многочлен
Рассмотрим многочлен
где
Если комплексное число
то сопряженное число
Так как сумма
Следствие 3. Если комплексное (но не действительное) число
В самом деле, если
Из условий
Следствие 4. Всякий многочлен
где
Следствие 5. Многочлен нечетной степени с действительными коэффициентами всегда имеет хотя бы один действительный корень.
Многочлен четной степени с действительными коэффициентами может не иметь действительных корней (при этом в разложении (В. 14) отсутствуют линейные двучлены
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.240.21 (0.042 с.) |



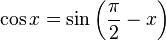
 или
или 

 или
или 



 или
или 

 , которые являются следствием формулы Эйлера. Мнимая единица j отличается от мнимой единицы i только обозначением. В пространстве Y эта единица фиксирует третье координатное направление. Алгебра этой единицы совпадает с алгеброй мнимой единицы i. Поэтому в силе остаются и формулы
, которые являются следствием формулы Эйлера. Мнимая единица j отличается от мнимой единицы i только обозначением. В пространстве Y эта единица фиксирует третье координатное направление. Алгебра этой единицы совпадает с алгеброй мнимой единицы i. Поэтому в силе остаются и формулы Далее формулы распространяются в пространство
Далее формулы распространяются в пространство 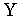 .
. При переходе от
При переходе от  к
к 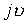 получаем гиперболические функции в пространстве Y.
получаем гиперболические функции в пространстве Y.



 ,в силу комплексности переменной
,в силу комплексности переменной 

 . Аналогичные преобразования дают
. Аналогичные преобразования дают

 ,
,  И т. п.
И т. п. И
И  Считают равными и пишут
Считают равными и пишут  В том и
В том и И
И  Можно найти такие многочлены
Можно найти такие многочлены  И
И  , что
, что (8.1)
(8.1) Меньше степени
Меньше степени  Или же
Или же  . Многочлены
. Многочлены 
 Определяются однозначно.
Определяются однозначно. Называется частным от деления
Называется частным от деления  На
На  , а
, а  -
-
 На
На  Равен нулю, то многочлен
Равен нулю, то многочлен  Называется делителем многочлена
Называется делителем многочлена  , в этом случае говорят, что
, в этом случае говорят, что  Делится на
Делится на  (или нацело делится на
(или нацело делится на  ).
). Тогда и только тогда является делителем многочлена
Тогда и только тогда является делителем многочлена 
 Удовлетворяющий равенству
Удовлетворяющий равенству
 Называется общим делителем для многочленов
Называется общим делителем для многочленов  И
И , если он является делителем каждого из этих многочленов.
, если он является делителем каждого из этих многочленов. И
И  называется общий делитель
называется общий делитель 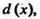 Который делится на любой другой общий де
Который делится на любой другой общий де И
И Обозначается так:
Обозначается так: 
 И
И  Можно найти с по
Можно найти с по
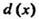 — наибольший общий делитель многочленов
— наибольший общий делитель многочленов  И
И  То
То  , где
, где  - любое 'число, отличное от
- любое 'число, отличное от на двучлен
на двучлен  равен
равен  .
. - корень многочлена
- корень многочлена  .
. .
. число
число 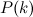 делится на
делится на  .
. , то заданный многочлен
, то заданный многочлен 
 , степень которого на единицу меньше степени исходного многочлена. Иногда этим приемом - он называется понижением степени - можно найти все корни заданного многочлена.
, степень которого на единицу меньше степени исходного многочлена. Иногда этим приемом - он называется понижением степени - можно найти все корни заданного многочлена.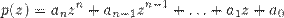 степени
степени  с комплексными коэффициентами
с комплексными коэффициентами 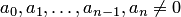 можно представить в виде произведения линейных двучленов:
можно представить в виде произведения линейных двучленов: — корни многочлена кратности
— корни многочлена кратности  соответственно, причем
соответственно, причем  . Другими словами, многочлен n-й степени имеет ровно
. Другими словами, многочлен n-й степени имеет ровно  корней, если каждый корень считать столько раз, какова его кратность.
корней, если каждый корень считать столько раз, какова его кратность. и
и  , степени которых не превосходят
, степени которых не превосходят  , то эти многочлены равны:
, то эти многочлены равны:  .
. имеет более, чем
имеет более, чем 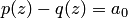 . Так как он имеет корни, то
. Так как он имеет корни, то  . Следовательно,
. Следовательно,  , то есть
, то есть 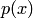 не как формальное выражение вида (В.8), а как функцию переменной
не как формальное выражение вида (В.8), а как функцию переменной  , поскольку равенство многочленов
, поскольку равенство многочленов  , определенное выше как равенство коэффициентов при одинаковых степенях
, определенное выше как равенство коэффициентов при одинаковых степенях  двух функций при всех значениях
двух функций при всех значениях  с действительными коэффициентами
с действительными коэффициентами 
 — корни многочлена (могут быть комплексные).
— корни многочлена (могут быть комплексные). является корнем этого многочлена, то есть
является корнем этого многочлена, то есть
 также является его корнем, т.е.
также является его корнем, т.е.  . Это вытекает из равенства
. Это вытекает из равенства  . Поскольку числа
. Поскольку числа 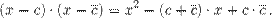
 и произведение
и произведение  сопряженных чисел являются действительными числами, то правая часть последнего равенства есть квадратный трехчлен с действительными коэффициентами. Причем, если
сопряженных чисел являются действительными числами, то правая часть последнего равенства есть квадратный трехчлен с действительными коэффициентами. Причем, если  , то дискриминант этого квадратного трехчлена отрицательный.
, то дискриминант этого квадратного трехчлена отрицательный.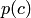 с действительными коэффициентами, то сопряженное число
с действительными коэффициентами, то сопряженное число  , то для него выполняются условия (В.12)
, то для него выполняются условия (В.12)
 с действительными коэффициентами представляется в виде произведения линейных двучленов и квадратных трехчленов (с отрицательными дискриминантами):
с действительными коэффициентами представляется в виде произведения линейных двучленов и квадратных трехчленов (с отрицательными дискриминантами): .
. ).
).


