
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое определение вероятности
Пусть теперь рассматривается непрерывная вероятностная схема, т.е. пространство элементарных исходов представляет собой некоторую ограниченную область (отрезок, круг, шар и т.д.) k ‑мерного пространства (прямой, плоскости, трёхмерного пространства и т.д.). В непрерывном случае число элементарных исходов бесконечно, следовательно, при использовании принципа равновероятности каждому элементарному исходу можно приписать только нулевую вероятность. Поэтому подойдём к определению геометрической вероятности по-другому. Рассмотрим сначала отрезок В общем случае геометрическая вероятность определяется аналогично. Пусть Определение. Геометрической вероятностью называют отношение меры области
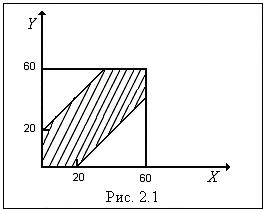
Пример 8. (Задача о встрече.) Два лица m Решение. Обозначим момент прихода лица Исходы, благоприятствующие встрече, изображены в заштрихованной области (рис. 2.1).
Искомая вероятность равна отношению площади заштрихованной области к площади всего квадрата
Пример 9. В круг радиуса
m Решение. Первый способ. Пусть
Второй способ. Рассмотрим полярную систему координат, в которой положение точки определяется углом
Итак, мы получили в одной и той же задаче два разных ответа. Причина заключается в том, что понятие геометрической вероятности не инвариантно относительно преобразований рассматриваемой области Отметим, что для нас предпочтительнее первый способ решения. l
Глава 3. Условная вероятность. Независимость событий.
Условная вероятность
Рассмотрим следующий пример. Бросаются две игральные кости. Найдем вероятность того, что сумма выпавших очков равна 8, если заранее известно, что сумма выпавших очков есть четное число. Всевозможные исходы запишем в виде таблицы 3.1: Таблица 3.1
Из таблицы видно, что число всевозможных исходов равно 36, но число исходов, удовлетворяющих условию, при которых сумма очков есть четное число, равно 18. Из них ровно в 5 исходах сумма очков равна 8. Пользуясь классическим определением вероятности, находим, что искомая вероятность равна Заметим, что безусловная вероятность того, что сумма выпавших очков, равная 8, равна Найдем условную вероятность
Разделив числитель и знаменатель на число всевозможных исходов
Последняя формула может служить общим определением условной вероятности при аксиоматическом подходе.
Определение. Условной вероятностью
Пример 1. При трехкратном подбрасывании монеты выпало два «герба». Найти условную вероятность того, что при втором подбрасывании выпал «герб». m Решение. Рассмотрим следующие события:
Событию Число всевозможных исходов при трехкратном подбрасывании монеты
Аналогично, событию
Далее, применяя (3.1.1), получаем искомую вероятность
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.13.201 (0.008 с.) |
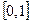 и предположим, что идеальная частица равномерно бросается на данный отрезок. Каждому интервалу
и предположим, что идеальная частица равномерно бросается на данный отрезок. Каждому интервалу 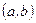
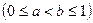 поставим в соответствие вероятность попадания частицы на этот интервал, равную его длине:
поставим в соответствие вероятность попадания частицы на этот интервал, равную его длине: 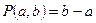 .
. - некоторая область, имеющая меру
- некоторая область, имеющая меру 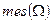 (длину, площадь, объём и т.д.) такую, что
(длину, площадь, объём и т.д.) такую, что 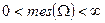 . Пусть внутри области
. Пусть внутри области  .
.
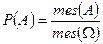 .
. договорились встретиться в определённом месте между 12 часами и часом. Пришедший первый ждёт другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц
договорились встретиться в определённом месте между 12 часами и часом. Пришедший первый ждёт другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц  , а момент прихода лица
, а момент прихода лица  . На плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60. Для того, чтобы встреча произошла необходимо и достаточно, чтобы выполнялось неравенство
. На плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60. Для того, чтобы встреча произошла необходимо и достаточно, чтобы выполнялось неравенство 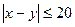 .
.
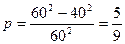 . l
. l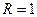 случайным образом бросается точка. Найти вероятность того, что точка попадёт в круг радиуса
случайным образом бросается точка. Найти вероятность того, что точка попадёт в круг радиуса 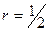 с тем же центром (рис. 2.2).
с тем же центром (рис. 2.2).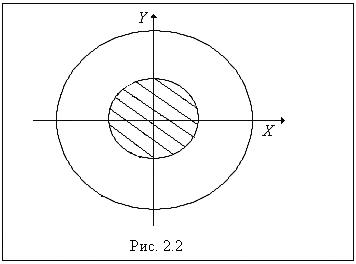
 как отношение площади малого круга к площади большего:
как отношение площади малого круга к площади большего: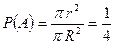 .
.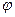 между радиус‑вектором точки и осью
между радиус‑вектором точки и осью 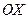 и расстоянием
и расстоянием 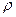 от точки до начала координат. Поскольку точки, равностоящие от центра, все либо одновременно принадлежат меньшему кругу, либо нет, то вероятность попадания в этот круг равна отношению радиусов:
от точки до начала координат. Поскольку точки, равностоящие от центра, все либо одновременно принадлежат меньшему кругу, либо нет, то вероятность попадания в этот круг равна отношению радиусов: 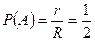 .
.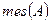 .
. .
. , т.е. задание дополнительного условия может повлиять на вычисление вероятности.
, т.е. задание дополнительного условия может повлиять на вычисление вероятности. события
события  уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов
уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов  , благоприятных совместному (одновременному) осуществлению событий
, благоприятных совместному (одновременному) осуществлению событий  .
.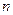 , получим:
, получим: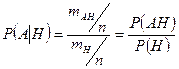 .
. . (3.1.1)
. (3.1.1) соответствует два исхода: Г – Г – Р, Р – Г – Г.
соответствует два исхода: Г – Г – Р, Р – Г – Г. . Отсюда находим:
. Отсюда находим: .
. .
. . l
. l


