
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Якщо не існує скінченої границі послідовності, то ряд називається розбіжним.
-Нехай маємо ряд Ряд вигляду Будь-який ряд Властивості збіжних рядів: Якщо
Якщо
Ознаки збіжності числових рядів з додатними членами Перша ознака порівняння. Нехай маємо ряди Із збіжності першого ряду випливає збіжність другого ряду. Із розбіжності другого ряду випливає розбіжність першого ряду. Гранична ознака порівняння. Нехай для членів рядів Доведення: (доведемо, що, якщо другий ряд розбігається, то перший також розбігається): Для будь-якого : Ознака Д’Аламбера. Радикальна та Інтегральна ознаки Коші. Ознака Д’Аламбера. Якщо для ряду Радикальна ознака Коші. Якщо для ряду Доведемо, що ряд збіжний при Для будь-якого
Інтегральна ознака Коші. Таким чином, якщо ряд збіжний, то збіжним є і невласний інтеграл Отже, розглянутий вище ряд та невласний інтеграл першого роду збіжні чи розбіжні одночасно.
Знакозмінні ряди. Ознака Лейбніца. Означення: Ряд називається знакозмінним, якщо серед його членів є як невід’ємні, так і від’ємні числа. Ознака Лейбніца: Нехай члени знакопочережного ряду прямують до нуля, складаючи при цьому спадну за абсолютною величиною послідовність, тоді такий ряд є збіжний. Доведення: Розглянемо ряд Розглянемо частинні суми окремо з парними і окремо з непарними номерами:
Знакозмінні ряди. Абсолютно і умовно збіжні ряди, їх властивості. Знакозмінний ряд є збіжним абсолютно, якщо збігається ряд складений з абсолютних величин його членів. Якщо знакозмінний ряд збіжний, але ряд складений з абсолютних величин його членів розбіжний, то такий ряд називається збіжним умовно. Властивості АЗР, можна сказати, що вони такі ж як у рядів з додатними членами: Якщо
Якщо
Якщо ряд є абсолютно збіжний, то довільний ряд, утворений з нього перестановкою його членів також є абсолютно збіжний. Властивості УЗР: В УЗР кількість додатних та від’ємних членів нескінченна; Ряди складені з сум додатних та від’ємних членів УЗР – розбіжні; Теорема Рімана: якщо знакозмінний ряд є збіжним, то шляхом перестановки його членів, його суму можна зробити рівною будь-якому наперед заданому числу. Функціональні ряди. Нехай
Означення: Функціональна послідовність (функціональний ряд) називається рівномірно збіжною (рівномірно збіжним) на деякому інтервалі Ознака Вейєрштраса: Нехай для ряду Доведення:
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.15.1 (0.01 с.) |
 , тоді
, тоді  , де
, де  та
та  . У збіжних рядів загальний член ряду завжди прямує до нуля при
. У збіжних рядів загальний член ряду завжди прямує до нуля при  . Це називається необхідною умовою збіжності. Відповідно можна стверджувати, що коли загальний член ряду не прямує до нуля ряд є розбіжним. Це називається достатньою ознакою розбіжності.
. Це називається необхідною умовою збіжності. Відповідно можна стверджувати, що коли загальний член ряду не прямує до нуля ряд є розбіжним. Це називається достатньою ознакою розбіжності. називається гармонічним. Таким чином маємо
називається гармонічним. Таким чином маємо  в результаті чого залишок суми ряду завжди більший за 1/2, а отже у відповідності до критерію Коші ряд є розбіжним. Ряд вигляду
в результаті чого залишок суми ряду завжди більший за 1/2, а отже у відповідності до критерію Коші ряд є розбіжним. Ряд вигляду 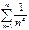 називається узагальненим гармонічним.
називається узагальненим гармонічним.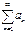 можна записати у вигляді
можна записати у вигляді 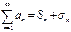 , де
, де  ,
,  при цьому величина
при цьому величина  називається залишком (хвостом) ряду.
називається залишком (хвостом) ряду. , то
, то 

 і
і  , то
, то 
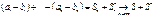
 , де
, де  та
та  , де
, де  та
та  .
. та
та  , при цьому для всіх значень
, при цьому для всіх значень  виконується нерівність
виконується нерівність  , тоді:
, тоді: та
та 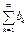 існує скінченна границя
існує скінченна границя  , причому
, причому  . Тоді ці ряди збігаються або розбігаються одночасно.
. Тоді ці ряди збігаються або розбігаються одночасно.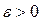 знайдеться такий номер
знайдеться такий номер  починаючи з якого
починаючи з якого  , де
, де  . Таким чином
. Таким чином  . Отже відповідний „хвіст” першого ряду більший за хвіст другого ряду помноженого на
. Отже відповідний „хвіст” першого ряду більший за хвіст другого ряду помноженого на  . Оскільки відповідно до критерію Коші „хвіст” другого ряду не прямує до нуля, то не прямує до нуля і „хвіст” першого ряду, що свідчить про його розбіжність.
. Оскільки відповідно до критерію Коші „хвіст” другого ряду не прямує до нуля, то не прямує до нуля і „хвіст” першого ряду, що свідчить про його розбіжність.
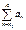 , існує границя
, існує границя 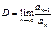 , то при
, то при  - ряд розбіжний; при
- ряд розбіжний; при  - ряд збіжний; при
- ряд збіжний; при  - ряд вимагає дослідження за допомогою інших ознак.
- ряд вимагає дослідження за допомогою інших ознак. існує границя
існує границя  , то при
, то при  - ряд розбіжний, при
- ряд розбіжний, при  - ряд збіжний і при
- ряд збіжний і при 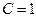 - ряд потребує подальшого дослідження іншим методом.
- ряд потребує подальшого дослідження іншим методом. , існує таке
, існує таке 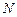 , що при
, що при 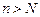
 , звідси виходить, що
, звідси виходить, що 
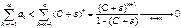 , що й треба було довести
, що й треба було довести
 ;
;  ;
; 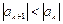 , припустимо, що додатними є члени ряду з непарними номерами
, припустимо, що додатними є члени ряду з непарними номерами  ,
,  ,
,  ,...; а від’ємними – члени ряду з парними номерами:
,...; а від’ємними – члени ряду з парними номерами: 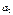 ,
,  ,
,  ,....
,....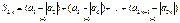 , отже у випадку частинних сум з парними номерами ми маємо зростаючу послідовність, в той же час
, отже у випадку частинних сум з парними номерами ми маємо зростаючу послідовність, в той же час , тобто ця послідовність обмежена зверху, і, відповідно, прямує до певної границі:
, тобто ця послідовність обмежена зверху, і, відповідно, прямує до певної границі: . Оскільки
. Оскільки  то
то  , що й треба було довести.
, що й треба було довести. , то
, то 
 , то
, то 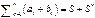

 , де
, де 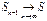 та
та  , де
, де  та
та  .
. послідовність функцій. Якщо при фіксованому значенні числова послідовність
послідовність функцій. Якщо при фіксованому значенні числова послідовність  є збіжною до числа
є збіжною до числа  , то кажуть, що число
, то кажуть, що число  належить області збіжності вказаної послідовності. Сукупність значень
належить області збіжності вказаної послідовності. Сукупність значень  при яких послідовність є збіжною, називається областю збіжності даної послідовності, а функція
при яких послідовність є збіжною, називається областю збіжності даної послідовності, а функція 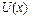 визначена для значень х із цієї області називається границею даної послідовності.
визначена для значень х із цієї області називається границею даної послідовності. до функції
до функції  . Якщо для будь-якого
. Якщо для будь-якого 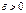 знайдеться
знайдеться  таке, що для будь-якого
таке, що для будь-якого  при
при  виконується нерівність
виконується нерівність  або
або 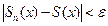 .
.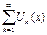 існує збіжний числовий ряд
існує збіжний числовий ряд  , такий що при всіх значеннях
, такий що при всіх значеннях  і довільних
і довільних  з інтервалу
з інтервалу  виконується нерівність:
виконується нерівність:  , тоді функціональний ряд збігається рівномірно для
, тоді функціональний ряд збігається рівномірно для  .
.


