
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Регрессионные модели с переменной структурой ⇐ ПредыдущаяСтр 5 из 5
5.1 Сущность и особенности использования фиктивных переменных 5.2 Модели ANOVA и ANCOVA 5.3 Вычисление параметров регрессионной модели с переменной структурой при помощи МНК 5.4 Оценка качества регрессионной модели с переменной структурой 5.5 Модели с фиктивной зависимой переменной Основные положения Часто возникает необходимость учета в регрессионной модели факторов, не имеющих количественного выражения. Например, при анализе динамики производства по месяцам следует учитывать сезонную компоненту. При анализе потребительских предпочтений может возникнуть задача учета пола потребителя, его отношения к определенной социальной группе. При регрессионном анализе предприятий может возникнуть потребность учета его формы собственности, отрасли, к которой предприятие относится. Модели, в которых учитываются подобные атрибутивные признаки, называются моделями с переменной структурой. Для решения проблемы учета таких факторов можно: 1. Составить несколько регрессионных моделей, каждая из которых отражает зависимость в качественно однородной среде. Это приведет к значительному усложнению как непосредственно расчетов, так и интерпретации результатов. 2. Добавить в модель фиктивные переменные. Эти переменные могут принимать только два значения: 1, если наблюдается определенное значение признака, и 0, если оно не наблюдается. При этом количество переменных для включения одного признака будет на 1 меньше числа значений, принимаемых этим признаком. Пример: Рассмотрим регрессионную модель влияния на рентабельность активов различных факторов. Если необходимо учесть влияние фактора «организационно-правовая форма», то следует добавить следующие фиктивные переменные:
(предполагается, что круг рассматриваемых предприятий ограничивается только тремя организационно-правовыми формами: ОАО, ЗАО и ООО). Как несложно заметить, число фиктивных переменных можно сократить, так как всегда будет выполняться равенство:
В общем случае построенная с включением фиктивных переменных регрессионная модель может иметь вид: а)
б) Можно выделить три основных направления использования моделей с переменной структурой: моделирование сезонных колебаний, моделирование институциональных изменений и учет влияния на результативный признак качественных факторов (рис. 5.1). Учет сезонных колебаний осуществляется путем добавления 3 (если имеются квартальные данные) или 11 (если информация представлена по месяцам) фиктивных переменных. Учет институциональных изменений осуществляется путем добавления переменной, характеризующей данные как «до» и «после» изменений. Например, если рассматривается хозяйственная деятельность предприятия, и необходимо учесть влияние смены директора на его эффективность, то в модель необходимо добавить переменную z, такую, что:
При применении модели в анализе качественных признаков (таких, как пол, социальный статус, форма собственности и т.п.) использование фиктивных переменных осуществляется по стандартной схеме.
Рис. 5.1 Использование моделей с переменной структурой
Спецификация модели с переменной структурой обычно, в части фиктивных переменных, имеет вид линейной функции:
Однако в ряде случаев возможно использование альтернативной фиктивной переменной (т.е. принимающей только два значения) в мультипликативной функции вида:
Спецификация (5.6) используется, когда явно можно предположить, что изменение фиктивной переменной отразится не только на изменении начального уровня явления и параллельном сдвиге линии регрессии, но и на ее наклоне. Такое предположение возможно, в частности, когда рассматривается зависимость заработной платы от стажа и пола сотрудников, или же при учете институциональных изменений. Последовательность решения задач эконометрического анализа моделей с переменной структурой после проведения спецификации модели не отличается от последовательности, применяемой в решении обычных задач множественной регрессии: это определение оценок неизвестных параметров при помощи МНК и оценка качества модели.
Обратите внимание, что для применения МНК необходимо выполнение его предпосылок, изложенных в теме 4. Для определения оценок параметров в модели (5.5) можно сразу использовать МНК. Если же используется модель вида (5.6), то следует либо рассматривать несколько регрессий, в которых значения фиктивных переменных заданы, либо преобразовать переменные путем замены (в случае одной фиктивной переменной):
Тогда спецификация модели изменится, и она примет вид обычной множественной регрессии:
Определение параметров в такой модели осуществляется при помощи обычного МНК, затем, в случае необходимости, можно вернуться к исходной форме. Оценка качества моделей с переменной структурой осуществляется по тому же алгоритму, что и для обычной множественной регрессии. Общую характеристику качеству построенной модели может дать коэффициент детерминации В том случае, если использовалась мультипликативная форма модели (5.5) с одной фиктивной переменной, для оценки качества модели может быть использован тест Чоу. Тест Чоу основан на F-критерии. Для его проведения необходимо построить регрессионную модель без участия фиктивной переменной (общую модель), рассчитать сумму квадратов отклонений фактических значений от общей модели. F-критерий рассчитывается как соотношение величины, на которую уменьшилась дисперсия в модели с переменной структурой по сравнению с общей моделью и дисперсии модели переменной структурой:
где
Полученное фактическое значение сравнивается с критическим Fα; m+1; n-2m-1. Если расчетное значение оказывается больше фактического, то считается, что использование фиктивной переменной целесообразно. Также фиктивная зависимая переменная может быть использована для интерпретации влияния на качественный признак количественных факторов. В этом случае говорят о фиктивной зависимой переменной. Различают несколько видов таких моделей: 1. Линейная вероятностная модель (linear probability model – LPM) 2. Модели бинарного выбора (LOGIT и PROBIT модели). Спецификация линейной вероятностной модели имеет вид (4.2) – если все объясняющие переменные описывают количественные факторы, или (5.5) – если в модели присутствуют фиктивные объясняющие переменные. Однако в этом случае зависимая переменная y может принимать только одно из двух значений:
После расчета параметров модели по МНК расчетные значения зависимой переменной интерпретируются как вероятность того, что признак, характеризуемый y, будет наблюдаться. Однако применение этого метода ограничено тем, что:
1) не выполняется ряд предпосылок МНК (случайные остатки не распределены по нормальному закону, дисперсия остатков непостоянна); 2) возможна ситуация, когда расчетное значение y будет находиться вне области допустимых значений: [0,1]; 3) с содержательной точки зрения линейное изменение вероятности при изменении влияния факторов некорректно. Для преодоления последних двух условий разработаны и используются модели бинарного выбора, среди которых выделяют LOGIT и PROBIT модели. Рассмотрим суть LOGIT модели. В ней в качестве функции, характеризующей вероятность того, что y примет значение 1, рассматривается логистическая функция. Эта функция принимает значения строго от 0 до 1:
где
Однако для применения МНК необходимо выполнить преобразования, поскольку функция (5.11) не линейна относительно параметров. Из (5.11) следует:
Последнее выражение линейно относительно параметров, однако к нему нельзя применить МНК. Причина этого в том, что для фактических данных неизвестными остаются значения pi. Для их нахождения в случае сгруппированных данных возможно использование в качестве оценки относительную частость проявления Вопросы для самоконтроля 1. В каком случае возникает необходимость использования фиктивных переменных? Приведите примеры. 2. Какие значения принимает фиктивная переменная? От чего зависит то, какое значение она примет? 3. В чем состоит различие моделей ANOVA и ANCOVA? Какие модели чаще используются на практике? 4. Опишите основные направления использования моделей с фиктивными переменными. Приведите примеры. 5. Как выглядит спецификация ANCOVA – модели? 6. Когда используется мультипликативная форма модели ANCOVA? 7. Какая особенность применения МНК для расчета параметров модели в мультипликативной форме? 8. Каковы особенности оценки качества моделей с переменной структурой? 9. Для чего используется тест Чоу? 10. Какие виды моделей с фиктивной зависимой переменной Вы знаете? 11. Какие ограничения линейной вероятностной модели затрудняют ее применение? 12. Какая цель преследуется при построении LOGIT модели. Задания и задачи 1. Приведите пример модели с переменной структурой: a) ANOVA b) ANCOVA c) модели с фиктивной зависимой переменной Для каждой модели укажите количество фиктивных переменных и принимаемые значения
2. По приведенным в таблице данным постройте модель с переменной структурой.
В апреле 2001 на предприятия сменился директор. Рассмотрите различные варианты моделей. Какая из возможных моделей будет наиболее качественной? 3. По данным таблицы из предыдущего задания, используя подход «сверху вниз», постройте модель анализа факторов, влияющих на заработную плату работников фирмы. Выделите фиктивные переменные и покажите, каким образом они определяются. 4. Оцените качество модели с переменной структурой, если: m = 4 n = 50 Se2 = 1200 Sy2 = 10800 Se(z)2 = 1000 Есть ли необходимость в использовании фиктивных переменных? 5. По данным таблицы постройте LPM и LOGIT – модели и рассчитайте их параметры. Какова вероятность банкротства для предприятия если Кал = 0,002, Ктл = 1,2, рентабельность в прошлом году – (- 0,12), в текущем – (+0,07). Насколько качественна построенная модель.
6. Какова вероятность того, что удастся сдать экзамен на отлично, потратив на подготовку 2 дня, если в соответствующей LOGIT-модели z=-5+3x, где x – количество дней, затраченных на подготовку. Сколько дней нужно потратить, чтобы на 90% быть уверенным в отличной оценке. 7. В городе N была проведено исследование «честный кондуктор». В течение недели 3 респондента «случайно» давали за проезд кондуктору больше мелких монет, чем составляла стоимость проезда. Цель исследования – определить силу и характер влияния на то, вернет ли кондуктор «лишние» деньги, различных факторов. В результате получены следующие результаты:
Тесты 1. Для учета сезонных колебаний по квартальным данным число фиктивных переменных должно быть равно: a) 1 b) 3 c) 4 d) 5 2. Модели, в которых независимые переменные могут быть как количественные, так и фиктивные, называются: a) ANOVA b) ANCOVA c) LPM d) LOGIT 3. Какие из моделей с фиктивной зависимой переменной допускают ситуацию, когда значение фиктивной переменной выйдет за границы [0;1]: a) ANOVA b) ANCOVA c) LPM d) PROBIT 4. Сумма значений m фиктивных переменных, характеризующих один качественный признак, равна: a) 0 b) 1 c) m – 1 d) m 5. Мультипликативная форма модели с переменной структурой будет иметь вид: a) b) c) d) 6. Какой коэффициент лучше использовать для оценки качества модели с переменной структурой? a) R2 b) скорректированный R2 c) x0 d) rxy 7. Тест Чоу используется: a) Для расчета параметров регрессии b) Для оценки статистической значимости параметров c) Для оценки качества модели с фиктивной переменной d) Для определения структурных сдвигов 8. Для учета сезонных колебаний по квартальным данным число вводимых фиктивных переменных должно быть: a) 2 b) 3 c) 4 d) 5 9. Какая функция используется в LOGIT модели для описания вероятности принятия фиктивной переменной определенного значения? a) линейная b) логистическая c) логарифмическая d) экспоненциальная 10. Какая из формул используется в тесте Чоу? a) b) c) d) ни одна из перечисленных 11. Работники фирмы установили, что заработная плата сотрудника достаточно описывается моделью: y=3500 + 2200 z+ε, где z= a) LPM – моделью b) LOGIT – моделью c) ANCOVA – моделью d) ANOVA – моделью Список литературы 1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.ЮНИТИ, 1998. – с. 735 – 749; 766 – 772. 2. Бородич С.А. Эконометрика: Учебное пособие. – Мн.: Новое знание, 2001. – с. 285 – 302; 250 – 264 3. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – XIV, с. 262 – 285 4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – с. 115 – 122 5. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. 2-е изд. – М.: Дело, 1998. – с. 69 – 74 6. Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с. 49 – 105 7. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с.141 – 155
Пример проведения эконометрического исследования Задание 1. По представленным в таблице данным провести регрессионный анализ зависимости прироста сбережений населения от различных факторов. Таблица 1 Исходные статистические данные
1. Построение описательной экономической модели. Из экономической теории мы знаем, что денежные доходы населения влияют на величину сбережений. Также на величину сбережений влияет и процентная ставка. Однако нам дана информация только о приростах сбережений и доходов. Поэтому мы предполагаем, что на величину прироста сбережений влияют прирост денежных доходов и ставка по кредиту. 2. Исходя из сделанного предположения строим эконометрическую модель, которая относится к классу факторных статических моделей: y=f(x1,x2) где x1 – прирост денежных доходов (объясняющая переменная) x2 – ставка по кредиту (объясняющая переменная) y – прирост сбережений (зависимая переменная) Чтобы убедиться в том, что выбор объясняющих переменных оправдан, оценим связь между признаками количественно, для этого заполним матрицу корреляций (расчет выполнен по формуле 2.4):
Таблица 2. Матрица корреляций между исходными статистическими признаками
Анализируя матрицу корреляций, можем сделать вывод о наличии сильной положительной связи между приростами денежных доходов и сбережений. В то же время связь между ставкой процента и сбережениями практически не прослеживается. Поэтому модифицируем модель к виду парной регрессии: y=f(x1) Для выбора функциональной формы модели проанализируем корреляционное поле:
Визуальный анализ показывает, что для построения модели вполне подойдет линейная функция: y=α0 + α1x1 + ε 3. Оценка параметров модели. Проведем оценку параметров модели при помощи различных способов. Метод средних. Предположим, что изменение сбережений обусловлено только изменением денежных доходов (т.е. α0 = 0). Тогда оценка a1 неизвестного параметра α1 определится по формуле (3.5):
модель принимает вид: y=2,09x1+e Метод проб. В августе прирост денежных доходов был практически нулевым, при этом прирост сбережений составил 64,6 млрд. руб. Можно предположить, что это значение характеризует нулевой уровень зависимой переменной, т.е. ее значение, обусловленное действием прочих факторов. Тогда по формуле (3.6) рассчитаем оценку параметра α1:
в этом случае уравнение регрессии примет вид: y=64,6+0,10x1+e Метод выбранных точек. Проанализируем корреляционное поле и выберем точки, которые ближе всех лежат в предполагаемой прямой линии, описывающей модель. Это будут точки «сентябрь» Рассчитаем параметры модели по формулам (3.7) и (3.8):
уравнение регрессии выглядит следующим образом: y=54,2+0,43x1+e Метод наименьших квадратов. Для применения этого метода составим вспомогательную таблицу:
Составим систему для расчета значений параметров:
Решив эту систему, получаем значения a0 = 55,5 a1 = 0,38 Линия регрессии описывается уравнением: y=55,5+0,38x1+e Сведем полученные результаты в таблицу: Таблица 3 Уравнения регрессий, полученные при помощи разных методов
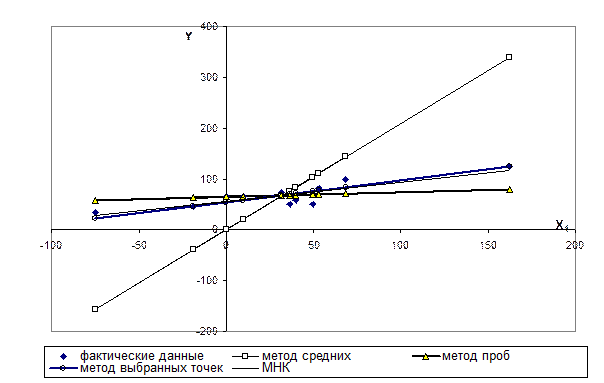
Покажем на графике различие между полученными линиями регрессии:
Рис. 2 Линии регрессии, полученные при помощи различных методов 4. Проверка качества построенной модели. Выполним оценку качества поэтапно. Оценку адекватности модели в целом проведем для каждой из выбранных моделей: Таблица 4. Предварительные расчеты для вычисления
Примечание: МС – метод средних МП – метод проб МВТ – метод выбранных точек МНК – метод наименьших квадратов На основе таблицы для каждой модели по формуле (3.25) рассчитаем значение дисперсий случайного остатка, а по формуле (3.26) – значения коэффициента детерминации. Результат запишем в таблицу: Таблица 5 Оценка адекватности моделей парной регрессии
Как видно из таблицы, наилучшее качество имеет модель, построенная по методу наименьших квадратов. Следующие этапы оценки качества проведем только для этой модели. Для нее расчетное значение F-критерия равно:
, а соответствующее критическое значение (приложение 3) – F0,05;1;9 = 5,117. Поскольку расчетное значение больше критического, то модель признается статистически значимой. Вычислим дисперсии оценок коэффициентов регрессии. Для этого воспользуемся формулами (3.30) и (3.31):
Стандартные ошибки коэффициентов регрессии будут равны:
Оценим статистическую значимость коэффициентов регрессии. Для этого рассчитаем t-статистику для каждого коэффициента (см. формулу 3.27):
Сравним с критическими значениями, взятыми из таблицы (приложение 2): Таблица 6 Критические значения t-статистики
Можно сделать вывод, что коэффициенты регрессии статистически значимы при 1 %-м уровне значимости. Оценим доверительные интервалы для коэффициентов регрессии при разных уровнях значимости. Для этого воспользуемся формулами (3.33) и (3.34). Результат расчета занесем в таблицу: Таблица 7 Доверительные интервалы для коэффициентов регрессии
Рассчитаем доверительные интервалы для зависимой переменной. Для этого воспользуемся формулами (3.35) – для расчета доверительного интервала для среднего значения и (3.36) – для расчета доверительного интервала для индивидуальных значений. Результаты расчета для 5 %-го уровня значимости представлены в таблице и на графиках: Таблица 8 Доверительные интервалы для зависимой переменной (уровень значимости – 5%)
Рис. 3. Доверительные интервалы для среднего значения зависимой переменной. Уровень значимости – 5 %.
Рис. 4. Доверительные интервалы для индивидуального значения зависимой переменной. Уровень значимости – 5 %
5. Коэффициент детерминации R2 достаточно высок (0,73), расчетное значение F-статистики для R2 (24,83) более чем в 4 раза больше критического (5,117), следовательно может использоваться на практике. В то же время существование необъясненной дисперсии предполагает возможность улучшить качество модели путем введения еще одной переменной. 6. Как показал расчет, устойчивой связи между изменением сбережений и процентной ставкой нет. Оценим силу связи между приростными величинами: изменением сбережений и изменением процентной ставки (табл. 9): Таблица 9 Расчет прироста процентных ставок
Обозначим прирост ставки по кредиту через Таблица 10 Матрица корреляций между
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.32 (0.178 с.) |
 (5.1)
(5.1)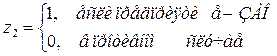 (5.2)
(5.2) (5.3)
(5.3) (5.4)
(5.4) – модели, содержащие только фиктивные объясняющие переменные, представляющие собой кусочно-постоянные функции (они называются ANOVA – моделями или моделями дисперсионного анализа)
– модели, содержащие только фиктивные объясняющие переменные, представляющие собой кусочно-постоянные функции (они называются ANOVA – моделями или моделями дисперсионного анализа) – модели, содержащие и количественные, и фиктивные объясняющие переменные, и называемые ANCOVA – моделями или моделями ковариационного анализа). Такие модели имеют вид множества функций, непрерывных на своей области определения. На практике чаще рассматриваются модели ANCOVA, в которых фиктивные переменные играют уточняющую роль.
– модели, содержащие и количественные, и фиктивные объясняющие переменные, и называемые ANCOVA – моделями или моделями ковариационного анализа). Такие модели имеют вид множества функций, непрерывных на своей области определения. На практике чаще рассматриваются модели ANCOVA, в которых фиктивные переменные играют уточняющую роль.

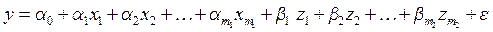 (5.5)
(5.5) (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) (поскольку модель множественной регрессии, то рекомендуется использовать скорректированный коэффициент детерминации
(поскольку модель множественной регрессии, то рекомендуется использовать скорректированный коэффициент детерминации  , рассчитываемый по формуле (4.7)). Статистическая значимость коэффициента детерминации может быть оценена при помощи F-критерия.
, рассчитываемый по формуле (4.7)). Статистическая значимость коэффициента детерминации может быть оценена при помощи F-критерия. (5.9)
(5.9) – сумма квадратов случайных отклонений в общей модели
– сумма квадратов случайных отклонений в общей модели – сумма квадратов случайных отклонений в регрессионной модели с переменной структурой
– сумма квадратов случайных отклонений в регрессионной модели с переменной структурой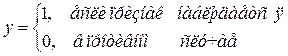 (5.10)
(5.10) (5.11)
(5.11)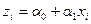
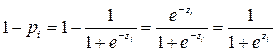 (5.12)
(5.12)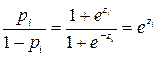 (5.13)
(5.13) (5.14)
(5.14) , в случае несгруппированных следует применять метод максимального правдоподобия.
, в случае несгруппированных следует применять метод максимального правдоподобия.

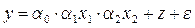



 / Построенная модель является:
/ Построенная модель является: Рис. 1 Корреляционное поле
Рис. 1 Корреляционное поле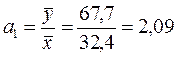















 . Матрица корреляций в этом случае будет иметь вид:
. Матрица корреляций в этом случае будет иметь вид:


