
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схемы программ и методы программной спецификации и верификацииСтр 1 из 4Следующая ⇒
Исследования алфавита В лексике языков программирования следует отметить, что все алфавиты, которые используются в языках программирования являются множествами и поэтому к ним очень часто применяют аппарат теории множества, в частности, если А и В являются алфавитами, причем А содержиться или равно В, то будем считать, что алфавит А является подалфавитом более широкого алфавита В. Или считается, что алфавит В является расширением алфавита А. Если в естественном языке совокупность символов называется словом, то в языках программирования совокупности символов алфавита называется более нейтральным термином – строки. И любую строку можно записать как а1, а2, …, аn. В языках программирования принято считать, что отдельные символы или буквы так же являются строками. Мы будем допускать случаи, когда отдельная строка не имеет символов (пустая строка) и обозначать эту строку греческой буквой лямбда. Заметим, что лямбда не является символом алфавита, а специально введена для возможности использования пустой строки. По аналогии с лингвистикой, иногда удобно строки иногда называть словами, множество всех строк над алфавитом А называется замыканием А и обозначают, как A*. A * = A’U A^2 U…A^n В том случае, когда мы не делаем ограничений на число символов в слове: А* = А^0 U … U A^n, n – бесконечность. Основная операция над строками – конкатенация. Формально, она может быть определена, как результат слияния 2х строк. Если строки состоят из повторяющихся букв, то в математической лингвистике принято сокращенное обозначение: пустая строка: a^0; aa=a^2; abaaa=aba^3. Традиционно программы для ЭВМ записываются в виде строк символов на некотором языке программирования. В настоящее время существует достаточно много языков программирования. Некоторые из них на современных вычислительных машинах уже не используются, поэтому по аналогии с лингвистикой все современные языки программирования делятся на живые и мертвые, причем необходимо помнить, что современные языки программирования постоянно развиваются и возможно появление в ближайшем будущем новых и еще более эффективных языков программирования. Наиболее изученным разделом математической лингвистики современных языков программирования является синтаксис. Именно синтаксис позволяет четко определять, принадлежит ли заданная последовательность символов правильным конструкциям языка.
Механизм проверки правильности цепочек символов необходим трансляторам. Транслятор, получая на входе программу в виде цепочки символов должен проверить, принадлежит ли она данному языку программирования. Если принадлежит, то транслятор переводит её в машинный код, иначе – сообщает программисту о предполагаемых ошибках.
4. Схемы программ. Табличные средства. Таблица - пример того, что в программировании называют широким термином структура данных, причём двумерная таблица проста и регулярна. Имена столбцов показывают в этом случае атрибутами, а также реквизитами, признаками, а строки записями или картежами. Саму таблицу показывают массивом записей. В неоднородной таблице столбцы (атрибуты) могут иметь разные типы: при этом элементы одного столбца имеют один и тот же тип, ассоциированный со столбцом, - его называют доменом. В таблице «сотрудники» типы столбцов могут быть ФИО, год и пол и представлять соответственно последовательность литер, целое число и букву. Операция упорядочения упорядочивает таблицу по значениям заданного атрибута. Что широко используется в электронных таблицах. Равенства и подстановки. Синтаксис равенства имеет вид L=R, где L и R - выражения, построенные из обозначений функций (операций), переменных и констант. L - называют левой частью равенства, a R - правой. Если тексты, содержащие выражения, должны обрабатываться машиной, храниться в машинной памяти, то это обычно накладывает дополнительные ограничения на синтаксис выражений, что небезразлично с точки зрения спецификации. Например, удобные и привычные для людей «многоэтажные» выражения приходится записывать как «одноэтажные», т.е вместо Х2, yi писать соответственно х*х, y[i] и т.д. Логические средства и аксиоматические описания. Под логическими средствами подразумеваются прежде всего способы точного формулирования утверждений и проведения правильных рассуждений, успешно применяемые в математической и научной практике. Утверждения записываются в логике в виде логических формул. В языках программирования логические формы называют логическими выражениями, в отличие от арифметических выражений они принимают только два истинностных значения, 0 или 1, true или false. Из первичных или атомных формул с помощью логических связок и кванторов строятся более сложные формулы. Важно, чтобы синтаксис логических выражений позволял однозначно восстанавливать смысл записываемых утверждений и был по возможности прост и удобен для восприятия и применения.
Потребности описания семантики языков программирования привели в последние годы к созданию целого семейства логик, называемых программными, алгоритмическими или динамическими. Существенной их особенностью является понятие состояния и понятие оператора (команды, программы), преобразующего одни состояния в другие (например, оператор присваивания). Самая известная среди них программная логика Хоара, формулы которой имеют вид P{S}Q, где Р и Q формулы логики, a S - оператор. Семантика такой формулы определяется следующим образом. Пусть заданы оператор S и интерпретация формул Р и Q. Тогда формула P{S}Q истинна, если для любого состояния σ, в котором формула Р истинна и результат σ‘ оператора S определен, формула Q истинна в состоянии σ’. Формулу Р называют предусловием, а σ- постусловием для оператора S. Графовые средства: графы, сети, диаграммы. Графовые средства - это математические понятия, имеющие дело с относительно простыми видами связей между объектами, которые допускают наглядное графическое изображение. Изображая связи линиями или стрелками, а объекты кружочками, получаем графическую картинку, представляющую объекты и связи. Важно, однако, четко осознавать, что за картинками стоят определенные математические понятия и что картинки -это только внешний способ представления понятий. По существу, картинки -это форма синтаксиса понятий, и для графовых средств она наиболее адекватна. Граф G={V,R} можно рассматривать, как двухместное бинарное отношение R на множестве V, которое определяется, как множество упорядоченных пар элементов множества V. Сетью называют любую графовую структуру, но чаще графы с каким-нибудь специальным свойством, оно соответственно оговаривается в определении сети. Диаграммой называют граф специального вида, чаще всего помеченный граф. Деревом называется объект или представление объекта, имеющего иерархическую структуру, как раз и выраженную этим деревом. Все деревья являются ациклическими графами. Конечный ациклический граф - это наглядный способ задания частичного прядка на конечном множестве элементов. Синтаксические диаграммы. Для описания синтаксиса языков программирования используются в основном два средства: БНФ (Бэкуса - Наура формы) и синтаксические диаграммы. Исторически первыми были БНФ. При разработке языка Алгол-60 рабочей группой Международной федерации по обработке информации (IFIP -International Federation on Information Processing) была придумана нотация в виде металингвистических формул для описания правил грамматики языка. Такие формулы позволяют во многих случаях компактно описывать языки. Например, условный оператор можно описать в виде:
(условный оператор)::= IF< условие) THEN < оператор) | ELSE (оператор) В БНФ знак «::=» читается «это есть» и разделяет левую и правую часть правил. Знак «I» (вертикальная черта) читается «или» и разделяет возможные альтернативы в правой части правила. Угловые скобки выделяют текст -название понятия языка (нетерминального символа). Это минимальные средства БНФ. Эти символы используются в правых частях правил и позволяют несколько упростить набор правил или избежать рекурсии. Сети Петри. Сеть Петри - это совокупность С=(Р, Т, I, О), где Р - множество позиций; Т - множество переходов; I - входная функция; О - выходная функция. Разные варианты сетей Петри используются для асинхронных и параллельных систем. 11. Графические методы спецификации.
Графовые средства - это математические понятия, имеющие дело с относительно простыми видами связей между объектами, которые допускают наглядное графическое изображение. Изображая связи линиями или стрелками, а объекты кружочками, получаем графическую картинку, представляющую объекты и связи. Важно, однако, четко осознавать, что за картинками стоят определенные математические понятия и что картинки -это только внешний способ представления понятий. По существу, картинки -это форма синтаксиса понятий, и для графовых средств она наиболее адекватна. Необходимо отличать графовые средства (связанные с графами) от графических (связанных с графиком), считая, что первые относятся к понятиям, а вторые к способам их изображения в виде рисунков. Граф G={V,R} можно рассматривать, как двухместное бинарное отношение R на множестве V, которое определяется, как множество упорядоченных пар элементов множества V. Говоря о бинарных отношениях, как о графах, просто имеют в виду возможность их визуального представления и использования характерных для графов методов и терминологии. Сетью называют любую графовую структуру, но чаще графы с каким-нибудь специальным свойством, оно соответственно оговаривается в определении сети. Диаграммой называют граф специального вида, чаще всего помеченный граф. Деревом называется объект или представление объекта, имеющего иерархическую структуру, как раз и выраженную этим деревом. Все деревья являются ациклическими графами. Конечный ациклический граф - это наглядный способ задания частичного прядка на конечном множестве элементов.
Графы (сети, диаграммы, деревья и т.д.) используются для целей спецификации не сами по себе, а с некоторой дополнительной информацией или структурой, которая обычно называется интерпретацией. Это может быть функция, язык, поведение сети в определенных ситуациях. Простейшим примером интерпретации может служить дерево вывода в КС-грамматике, т.е. последовательность символов (терминалов и нетерминалов), помечающих листья и образующих слово, для которого данное дерево является деревом вывода. Интерпретацией дерева выражения можно считать его семантику, т.е. правило вычисления выражения. 12.Автоматное преобразование информации Алгоритм является фундаментальной концепцией информатики, и вопрос построения автоматических устройств, реализующих алгоритмы, является одним из главных вопросов вычислительной техники. Хотя теория автоматов изучает достаточно простые модели, она является фундаментом большого числа разнообразных приложений. Эти приложения - от языковых процессоров до систем управления реального времени и протоколов связи микропроцессорных систем - покрывают значительную долю проблем, анализом и реализацией которых занимается информатика. В этом отношении можно привести слова Дуга Росса из компании Soft Tech, утверждавшего, что 80 или даже 90% информатики будет в будущем основываться на теории конечных автоматов. Результат преобразования информации вход —> выход зачастую зависит не только от того, какая информация появилась на входе, но и от того, что происходило раньше. Множество примеров этому дают биологические системы. Таким образом, существуют более сложные устройства, чем функциональные преобразователи информации (комбинационные автоматы); их реакция зависит не только от вектора входных сигналов в данный момент, но и от того, что было на входе раньше, от входной истории. Такие преобразователи называются автоматами с памятью или конечными автоматами. На один и тот же входной сигнал конечный автомат (КА) может реагировать по-разному, в зависимости от того, в каком состоянии он находится в данный момент. При получении входного сигнала КА не только выдает информацию на выход как функцию этого входного сигнала и текущего состояния, но и меняет свое состояние, поскольку входной сигнал изменяет его предысторию. Число входных историй счётно, но бесконечно. Если автомат будет вести себя по разному для каждой возможной предыстории, то он должен иметь бесконечный ресурс (память), чтобы все эти предыстории как-то запоминать. Если ввести на множестве предыстории отношение эквивалентности, то две предыстории можно считать эквивалентными, если они одинаковым образом влияют на дальнейшее поведение автомата. Очевидно, что для своего функционирования автомату достаточно запоминать класс эквивалентности, к которому принадлежит предыстория. Случай, когда количество таких классов эквивалентности конечно, является простейшим. Но именно такая математическая модель представляет значительный интерес и имеет большую практическую ценность. Соответствующая формальная модель называется конечным автоматом. В этой модели внутреннее состояние автомата представляет собой класс эквивалентности предыстории. Упрощенно можно считать, что внутреннее состояние автомата - это его характеристика, однозначно определяющая все последующие реакции автомата на внешние события. Однако, образно говоря, внутреннее состояние автомата - это всё то, что автомат знает о своем прошлом с точки зрения будущего поведения - его реакция на последующие входные сигналы. Можно сказать, что это его предыстория в концентрированном виде (класс эквивалентности предысторий) и реакция автомата на последующие сигналы определяется только текущим состоянием, но не тем, как автомат пришел в него. Конечный автомат - это устройство, работающее в дискретные моменты времени (такты). В каждом такте на вход КА подаются входные сигналы, а на выходе появляется выходной сигнал, зависящий от текущего состояния и поступившего входного сигнала. Моменты срабатывания (такты) определяются либо тактирующими синхросигналами, либо асинхронно, наступлением внешнего события, которое заключается в приходе сигнала. В этом случае говорят об управлении автомата событиями, и такты работы КА имеют различную длительность.
13. Основные понятия и определения теории конечных автоматов Рис 2.7 Передатчик
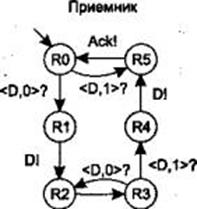
Рассмотрим протокол работы передатчика, изображенного на рисунке. Предположим, что автомат-передатчик находится в начальном состоянии S0 и ждет от пользователя порцию данных D, получив которую он переходит в новое состояние S1. В этом состоянии передатчик передает данные в канал связи нумеруя это сообщение D01, и включает таймер t. В состоянии S2, если до срабатывания таймера придет подтверждение правильной передачи Ack, то передатчик перейдет в состояние S3, в противном случае, в состоянии S2 при исчерпании времени работы таймера, он возвращается в состояние S1, и повторно передает сообщение с данными D0. Если он получил подтверждение и находится в состоянии S3, то передатчик снова ожидает событие ввода данных от пользователя, и, получив их, переходит в состояние S4, в котором передает сообщение с номером D1. Если передача завершилась успешно, то в состоянии S5 передатчик ожидает подтверждение от приемника, о получении этого сообщения. Если подтверждение получено, то из положения S5 автомат переходит в положение S0 и цикл передачи повторяется из состояния S0. Если, до срабатывания таймера t, установленного при входе автомата в состояние S5, передатчик не получит подтверждение о приемы предыдущего сообщения, то это сообщение посылается вновь. Аналогично работает приемник. 17. Конечный автомат как модель взаимодействия процессов.
Широко применяемым расширением классической модели конечного автомата являются диаграммы состоянии (Statecharts), введенные Д. Харелом в [8]. Мы рассмотрим две возможности таких «карт состояний». Первая — это гиперсостояние, объединяющее несколько состояний, имеющих идентичную реакцию на одно и то же событие. Вторая возможность — использование «исторического псевдосостояния». Семантика такого состояния (оно обозначается Н) состоит в том, что управление при возврате в гиперсостояние передается тому состоянию, в котором система находилась последний раз прежде, чем она покинула данное гиперсостояние. Переходы между состояниями в такой модели вызываются либо условиями (наступлением истинности предиката над внутренними переменными автомата, например, условие исчерпания буфера), либо событиями. Событиями в диаграммах состояний являются внешние события автомата. Обычно это прием управляющих или информационных сообщений из окружающей среды. Исчерпание тайм-аута также является возможным событием в этом расширении конечно-гоавтомата.
На рис. 3.17, а специфицируется прерывание системы в результате ошибки из любого состояния, принадлежащего гиперсостоянию Working, в состояние Crashed. После восстановления (Recovery) система продолжает работу из того состояния, в котором ее прервал сигнал Crash. В настоящее время модель состояний и переходов интенсивно используется для представления поведения параллельных взаимодействующих процессов.
Параллельные процессы характерны тем, что они функционируют независимо, но при этом должны согласовывать свои действия в определенные моменты для достижения некоторой общей цели. Такие процессы называются кооперирующими, взаимодействующими.
18. Автоматы Мура и Милли. Различают автоматы Мура и автоматы Милли. Автомат Мура является частным случаем более широкого понятия – автомата Мили. Автоматы Мура описываются следующими функциями переходов и выходов: Si+1 = f(Si, xi+1) yi+1 = f(Si+1) Каждое новое состояние автомата Мура обусловлено предшествующим состоянием и входным сигналом, а выходная функция – в каждый данный момент времени однозначно определяется состоянием автомата. Автоматы Мили отличаются от автоматов Мура тем, что выходной сигнал в этом автомате зависит не только от состояния, но и от входного сигнала. Si+1 = f(Si, xi+1) yi+1 = y(si, xi+1) Понятие внутреннего состояния автомата предполагает наличие у автомата внутренней памяти. Число различных эквивалентных состояний зависит от глубины памяти. В качестве элементов памяти могут использоваться стандартные модули ПЗУ или логические схемы с обратными связями в частности – различные типы триггеров.
В принципе любой автомат Мура можно свести к автомату Мили и наоборот. Автомат Мили – более универсальное устройство У автомата Мили нет таких ограничений, которые есть у Мура
Пример конечного автомата Мура представлен на рис. 3.9, а. Здесь выход автомата определяется однозначно тем состоянием, в которое автомат переходит после приема входного сигнала. Например, в состояние si можно прийти по трем переходам: из состояния sO под воздействием Ь, из состояния s2 под воздействием Ь, из состояния si под воздействием а. Во всех трех случаях выходная реакция автомата одна и та же: выходной сигнал у2. Очевидно, что по любому автомату Мура легко построить эквивалентный ему авто-мат Мили; для автомата Мура (рис. 3.9, а) эквивалентный ему автомат Мили изображен на рис. 3.9, б. 19. Примеры конечных автоматов.
Текущее состояние автомата представляет все то, что автомат знает о прошлом с точки зрения его будущего поведения — реакций на последующие входы. Эта история в концентрированном виде определена текущим состоянием, и все будущее поведение автомата, как реакция его на последующие входные сигналы, определено именно текущим состоянием, но не тем, как автомат пришел в него. Итак, конечный автомат — это устройство, работающее в дискретные моменты времени (такты). На вход конечного автомата в каждом такте поступает один из возможных входных сигналов, а на его выходе появляется выходной сигнал, являющийся функцией его текущего состояния и поступившего входного сигнала. Триггер так же является простейшим автоматом. Рассмотрим два типа триггеров: RS-триггер и счетный триггер. Состояние этих автоматов является их выходом, то есть это автоматы Мура. В RS-григгере два входа: Reset и Set. Вход Reset сбрасывает, a Set устанавливает единичное состояние автомата. В счетном триггере единственный счетный вход переключает автомат из нулевого состояния в единичное и обратно.
20. Программная и аппаратная реализация конечных автоматов.
Программная: Ниже приведена реализация конечного автомата, который прибавляет 1 к числу, поданному на вход в виде двоичной записи начиная с младшего разряда. #include <stdio.h> int c;
int main() { goto s1;
s2: c = getchar();
switch(c) { case EOF: exit(0); default: putchar(c); goto s2; } s1: c = getchar(); switch (c) { case EOF: exit(0); case '1': putchar('0'); goto s1; case '0': putchar('1'); goto s2; }
}
Апааратная:
Триггер так же является простейшим автоматом. Рассмотрим два типа триггеров: RS-триггер и счетный триггер. Состояние этих автоматов является их выходом, то есть это автоматы Мура. В RS-григгере два входа: Reset и Set. Вход Reset сбрасывает, a Set устанавливает единичное состояние автомата. В счетном триггере единственный счетный вход переключает автомат из нулевого состояния в единичное и обратно.
21. Сети Петри: принципы построения. Назначение СП: Анализ, моделирование и представление причинно-следственных связей в сложных системах параллельно действующих объ- ектов. Сети Петри были разработаны для моделирования дискретных систем, которые содержат взаимодействующие и параллельно работающие компоненты. Особенно эффективно сети Петри могут быть использованы при моделировании аппаратного и программного обеспечения ЭВМ, моделирования работы гибких производственных систем, а так же моделирования сложных биологических и социальных систем.
Впервые математический аппарат в виде сетей Петри предложил немецкий ученый Карл Адам Петри в своей докторской диссертации «Связь автоматов», которую он защитил в 1962 году. Работа Карла Адама Петри так и оставалась бы академическим исследованием, если бы на эту работу не обратила внимание группа исследователей, работавших под руководством Джорджа Девиса в Массачушесецком технологическом институте. Эта группа использовала математический аппарат, предложенный Петри и применила для работы над проектом MAC. Эта группа внедрила научные исследования, по математическому аппарату сети Петри было сделано много публикаций, которые с этим пор стали широко использоваться. Группа под руководством Джорджа Девиса предложила ряд дополнений и усовершенствований математического аппарата, предложенного Петри, именно в такой форме сети Петри вошли в широкую научную практику.
Полная оценка и использование математического аппарата сетей Петри требует хорошей математической подготовки, что является основным требованием для современного программиста. Современный инженер-програмист должен обладать необходимой математической подготовкой и достаточной квалификацией, чтобы использовать сети Петри как в повседневной инженерной работе, так и в научных исследованиях.
Входы и выходы переходов - комплекты. Комплект - обобщение множества, в которое включены повторяющиеся элементы. Математический аппарат теории сетей Петри основан на теории Комплекта. Теория комплектов является дальнейшим научным развитием теории множеств. Теорию множеств была предожена Георгом Кантером на первом всемирном конгрессе математиков в 1900 году. Георг Кантер определил множество четко и лаконично: «Множество есть многое, мыслимое как единое». Для описания операций с множествами Кантер предложил особый математический аппарат, который в последствии получил название алгебра Кантера. В теории множеств элемент может или принадлежать множеству M или не принадлежать этому множеству. Комплект является набором предметов из некоторой области, в отличие от множества комплекты допускают наличие нескольких экземпляров одного и того же элементы. В отличие от множества, где любой элемент может или не входить в множество или входить в него один только раз, комплект допускает вхождение любого элемента заданное число раз. Пусть область представляет собой совокупность элементов {a, b, c, d}, тогда над этой можно образовать комплект: b1 = {a, b, c}, b2 = { a,d} b3 = {a, a, b, b}, b4 = {a, b, a, b} Таким образом комплекты b1 и b2 являются множествами, комплекты b3 и b4 равны между собой. Так как в комплекте, как и в множестве порядок перечисления элемента не имеет значения. Основным понятием теории комплектов является функция числа вхождения данного экземпляра в комплект. Обозначение #(x, B) означает количество вхождения элемента в комплект B, то есть число экземпляров x в комплекте B. Если ограничить число элементов в комплекте следующим образом: 0 <= #(x, B) <= 1, то все комплекты будут множествами. Элемент x является членом комплекта B, если #(x, B) > 0 Так же как и в теории множеств, в теории комплектов существует пустой комплект, не содержащий элементов.
#(x, B) = 0 В пустом комплекте для всех элементов x содержание элементов равно нулю. Под мощностью |B| понимается количество всех элементов |B| = сигма(индекс x)(x,B)
Комплект А является подкомплектом, если для любого элемента х, количество каждого элемента в копмлекте А меньше, чем комплекта В. A В предельном случае два комплекта равны тогда, когда количество любого элемента х в комплекте А равно количеству элементов х в комплекте В для всех х. A = B Комплект А строго включен в комплект В, если А меньше или равно В и А неравно В А Операции над комплектами В отличии от теории множеств, над комплектами определены 4 операции. Если заданы два комплекта А и В, то для них существуют следующие операции: 1) Объединение AUB: max(#(x,A), #(x,B)) Объединение комплектов отличается от объединения в теории множеств. 2) Пересечение А П B: min(#(x,A), #(x,B)) 3) Сумма А + В = #(x,A) + #(x,B)) 4) Разность А - В = #(x,A) - #(x,B)) В теории множеств – суммы и разности множеств не существует. В разности комплектов необходимо, чтобы число элементов в комплекте А было больше чем число элементов в комплекте В, т.к. число элементов в комплекте не может быть отрицательным. Можно показать, что объединение комплектов, пересечение комплектов и сумма комплектов как математические операции коммутативны и ассоциативны. Справедливо следующее соотношение: А П В A П В A – B |A U B| <= |A| + |B| |A + B| = |A| + |B| Доказать геометрическим методом или методом рассуждения. Назовем множество элементов, из которых составлены комплекты областью D. Пространство комплектов Dn – есть множество всех таких комплектов, что их элементы принадлежат D и ни один из элементов не входит в комплект более n раз. Иначе говоря, для любого комплекта можно записать соотношение: B Множество D 23. Структура сети Петри. Сеть Петри состоит из 4-ех компонентов, которые и определяют ее структуру: 1) Множество P (от слова position) 2) Множество переходов T (transition) 3) Входная функция I (in) 4) Выходная функция O (out) Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход Tj в множество позиций I(tj), называемых входными позициями перехода. Выходная функция O отображает переход Tj в множество позиций O(tj), называемых выходными позициями перехода. I: Tj à P O: Tj à P Определение: Сеть Петри С является четверкой мат. объектов C = (P, T, I,O), где: P = {p1,p2,…,pn} T = {t1, t2, …, tn} Множество позиций и переходов не пересекается. Входная функция является отображением перехода в множество позиций I: Tj à P Выходная O является отображением из конкретного перехода в множество позиций O: Tj à P Мощность множества P есть число N. А мощность множество T, если число M. Произвольный элемент из множества позиций P обозначается как pi (i = 1,2,…,n) Произвольный элемент T обознается, как tj. (j = 1,2,…,n) Входы и выходы переходов представляют из себя комплекты позиции. Кратность входной позиции для перехода tj есть число появления позиции pi во входном комплекте переходов: #(pi I(tj)) Аналогично, кратность выходной позиции pi для перехода tj есть число появлений позиции pi в выходном комплекте переходов: #(pi, O(tj)) Определение 3.2. Определим расширенную функцию I и выходную функцию O: #(tj I(pi) = #(pj O(tj)) #(tj O(pi) = #(pi I(tj))
[ОФТОПИК] Назовем множество элементов, из которых составлены комплекты областью D. Пространство комплектов Dn – есть множество всех таких комплектов, что их элементы принадлежат D и ни один из элементов не входит в комплект более n раз. Иначе говоря, для любого комплекта можно записать соотношение: B Множество D
24. Графы сети Петри. Графы сетей Петри
Для иллюстрации основных понятий теории сетей Петри удобным представлением является графическое представление сети Петри.
Теоретико - графовым представлением сети Петри двудольный (бинарный) ориентированный мультиграф.
Двудольность (бинарность) графа состоит в том, что вершины графического представления бывают двух типов: 1) В виде кружка обозначается позиция 2) В виде планки – изображается переход Причем дуги соединяют только вершины различных типов, т.е. кружок соединяется с только с планкой, планка соединяется только с кружком.
Ориентированные дуги соединяют позиции и переходы.
Дуга направленная от позиции pi к переходу tj определяет позицю, которая является входом перехода …: O à|
Выходная позиция указывается дугой от перехода к позиции
Кратные выходы, так же представлены кратными дугами.
Граф G = (V, A) сети Петри есть бинарный ориентированный мультиграф.
Где V = { v1, v2,…, vs } – множество вершин. A = { a1, a2,…, ar } – множество дуг.
ai = (vj, vk), где vj и vk
Множество V состоит из двух непересекающихся подмножеств P и T à vj ∈ P и vk ∈ T или vj ∈ T и vk ∈ P
Граф сети Петри являетс мультиграфом, т.к. он допускает существование кратных дуг. Количество кратных дуг специально оговаривается.
Определим V = P U T. Зададим множество А как комплект направленных дуг такой, что для всех pi c P и tj с T выполняются след. соотношения:
#((pi, tj), A) = #(pi, I(tj)) 25.Аналитическое и графическое представление сети Петри. Представление сети Петри в виде структуры и в виде графа
Пусть задана следующая структура сети Петри C = (P,T,I,O), n = 5, m = 4;
P = {p1,p2,p3,p4,p5} T = {t1,t2,t3,t4}
I(t1) = {p1} I(t2) = {p2, p3, p5} I(t3) = {p3}
O(t1) = {p2, p3, p5} O(t2) = {p5} O(t3) = {p4} O(t4) = {p2, p3}
На этой сети всегда можно составить структуру сети Петри. Оба представления сети Петри в виде структуры и в виде Графа эквивалентны. Их можно преобразовать в друг друга.
Расширенные функции:
I(p1) = {} I(p2) = {t1, t4} I(p3) = {t1, t4} I(p5) = {t1, t2}
O(p1) = {t1} O(p2) = {t2} O(p3) = {t2, t3} O(p4) = {t4} O(p5) = {t2}
[ОФТОПИК]Заметим, что в случае дуг большой кратности для представления используется пучок дуг, помеченный числом кратности, а не изображением всех дуг, как показано на рис. 3.6. O –8->| -12->
Маркировка ню есть присваивание фишек позициям сети Петри. Фишка – это одна из компонент сети Петри (подобно позициям и переходам). Фишки присваиваются позициям. Их количество при выполнении сети может изменяться. Фишки используются для отображения динамики системы.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.151.106 (0.281 с.) |

 На рис. 3.17 показано, как с помощью этих простых расширений удается наглядно представить сложное поведение.
На рис. 3.17 показано, как с помощью этих простых расширений удается наглядно представить сложное поведение.
 Опишем поведение родителя, отправившего сына в школу. Сын приносит двойки и пятерки. Отец не хочет хвататься за ремень каждый раз, как только сын получит очередную двойку, и выбирает более тонкую тактику воспитания. Задавать автомат удобно графом, в котором вершины соответствуют состояниям, а ребро из состояния s в состояние q, помеченное х/у, проводится тогда, когда автомат из состояния s под воздействием входного сигнала х переходит в состояние q с выходной реакцией у. Граф автомата, моделирующего умное поведение родителя, представлен на рис. 3.2..Этот автомат имеет четыре состояния {sO, si, s2, s3} и два входных сигнала — оценки, полученные сыном в школе: {2,5}. Начиная с начального состояния sO (оно помечено входной стрелкой), автомат под воздействием входных сигналов переходит из одного состояния в другое и выдает выходные сигналы — реакции на входы. Выходы автомата {уО,..., у5} будем интерпретировать как действия родителя так: y0: брать ремень; y1: ругать сына; у2: — успокаивать сына; уЗ: — надеяться; у4: — радоваться; у5: — ликовать. Сына, получившего одну и ту же оценку — двойку, ожидает дома совершенно различная реакция отца в зависимости от предыстории его учебы. Отец помнит, как его сын учился раньше, и строит свое воспитание с учетом его предыдущих успехов и неудач. Например, после третьей двойки в истории 2,2,2 сына встретят ремнем, а в истории 2, 2, 5, 2 — будут успокаивать. Каждая предыстория определяет текущее состояние автомата, при этом некоторые входные предыстории эквивалентны (именно те, которые приводят автомат в одно и то же состояние): история 2,2,5 эквивалентна пустой истории, которой соответствует начальное состояние.
Опишем поведение родителя, отправившего сына в школу. Сын приносит двойки и пятерки. Отец не хочет хвататься за ремень каждый раз, как только сын получит очередную двойку, и выбирает более тонкую тактику воспитания. Задавать автомат удобно графом, в котором вершины соответствуют состояниям, а ребро из состояния s в состояние q, помеченное х/у, проводится тогда, когда автомат из состояния s под воздействием входного сигнала х переходит в состояние q с выходной реакцией у. Граф автомата, моделирующего умное поведение родителя, представлен на рис. 3.2..Этот автомат имеет четыре состояния {sO, si, s2, s3} и два входных сигнала — оценки, полученные сыном в школе: {2,5}. Начиная с начального состояния sO (оно помечено входной стрелкой), автомат под воздействием входных сигналов переходит из одного состояния в другое и выдает выходные сигналы — реакции на входы. Выходы автомата {уО,..., у5} будем интерпретировать как действия родителя так: y0: брать ремень; y1: ругать сына; у2: — успокаивать сына; уЗ: — надеяться; у4: — радоваться; у5: — ликовать. Сына, получившего одну и ту же оценку — двойку, ожидает дома совершенно различная реакция отца в зависимости от предыстории его учебы. Отец помнит, как его сын учился раньше, и строит свое воспитание с учетом его предыдущих успехов и неудач. Например, после третьей двойки в истории 2,2,2 сына встретят ремнем, а в истории 2, 2, 5, 2 — будут успокаивать. Каждая предыстория определяет текущее состояние автомата, при этом некоторые входные предыстории эквивалентны (именно те, которые приводят автомат в одно и то же состояние): история 2,2,5 эквивалентна пустой истории, которой соответствует начальное состояние.


 B
B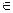 Dn
Dn есть множество всех комплектов над областью D без какого либо ограничения на число экзмеляров элементов в комплекте.
есть множество всех комплектов над областью D без какого либо ограничения на число экзмеляров элементов в комплекте. V
V



