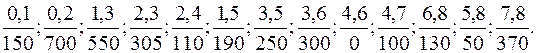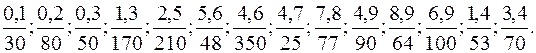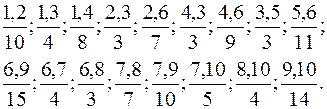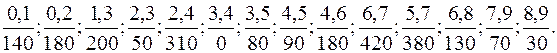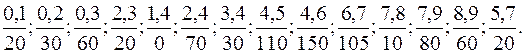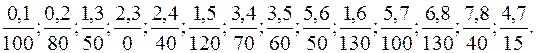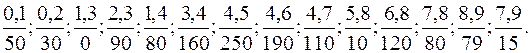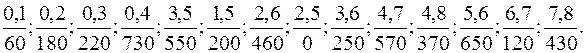Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фиксированной продолжительности критического пути ⇐ ПредыдущаяСтр 10 из 10
Предположим, что комплекс работ, описываемых сетевым графиком, необходимо выполнить в минимально возможные сроки. При составлении исходного сетевого графика в этом случае принимают, что продолжительность всех работ минимальная. Таким образом, обеспечивается наименьшая продолжительность критического пути, однако, общая стоимость всех работ имеет наибольшее значение. Задача состоит в следующем: не изменяя продолжительности критического пути, надо так продлить некритические работы, чтобы свести к минимуму стоимость выполнения всего комплекса работ. Рассмотрим методику оптимизации в упрощенной постановке. Допустим, что на максимальную продолжительность работ не наложены ограничения, следовательно, время выполнения каждой работы может быть увеличено в пределах ее полного резерва времени. Решение задачи рассмотрим на следующем примере. Пример: Пусть дан сетевой график с указанной на нем продолжительностью работ (рис. 3.12). Для каждой работы известны минимальная ее продолжительность
Характеристики работ сетевого графика Таблица 3.6
Обозначим R – множество работ критического пути, К – множество событий критического пути, R = {(1,3), (3,4), (4,6), (6,7)}, К = {1,3,4,6,7}. Для работ (i,j) Для рассматриваемого сетевого графика получим:
Продолжительность критического пути фиксирована, следовательно, фиксированы и моменты времени наступления событий, ему принадлежащих. Продолжительность некритических работ можно увеличить таким образом, чтобы моменты времени их завершения не выходили за пределы поздних сроков наступления соответствующих событий. Иначе говоря, продление некритических работ не должно привести к созданию в сетевом графике пути, продолжительность которого будет больше критической. Продолжительность работы можно определить как разность между сроками совершения начального и конечного для этой работы событий tij = ti – tj, поэтому в качестве неизвестных величин примем сроки наступления событий:
Выполнив замену переменных в формуле для определения стоимости работ, получим:
Определим ограничения для сроков наступления событий. Для событий критического пути Подставив в выражения, определяющие стоимость работ, значения
Целью задачи является минимизация стоимости выполнения всего комплекса работ при минимальной продолжительности критического пути, равной в рассмотренном примере 26 единицам времени. Для стоимости комплекса работ
На искомые неизвестные t2 и t5 наложены следующие ограничения:
Очевидно, что эти ограничения на сроки наступления событий 2 и 5 должны обеспечить работы (1,2), (3,5) и (5,7) временем, достаточным для их выполнения, поскольку начало работ (1,2) и (3,5) и завершение работы (5,7) определяются фиксированными моментами времени наступления событий критического пути. Для работы (2,5) неизвестными являются сроки как ее начала, так и завершения, поэтому их разность может оказаться меньше минимальной продолжительности работ Следовательно, задача оптимизации сетевого графика по стоимости свелась к задаче линейного программирования с ограничениями (3.1), (3.2) и функцией цели (3.3). На рис. 3.13 приведено решение этой задачи графическим способом. Из рисунка видно, что оптимальное решение равно t 2 = 13, t 5 = 20, С min = 431. Проанализируем полученные результаты. При минимальной продолжительности всех работ стоимость выполнения комплекса работ составляла
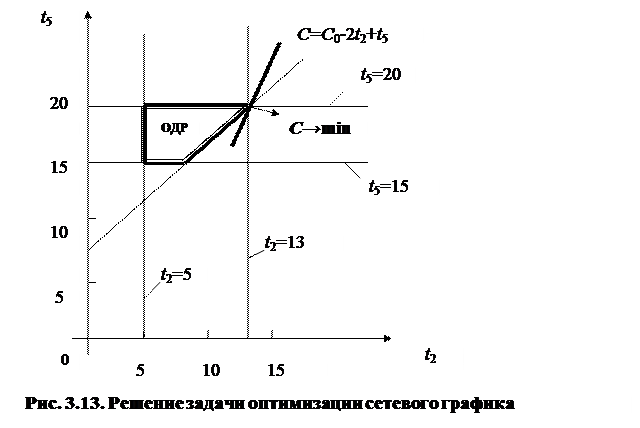
С = 530, что существенно больше значения С min. Работы (1,4) и (3,6) соединяют события критического пути и этим самым определяется их максимальная продолжительность
Продолжительность работ (1,2) и (3,5) увеличилась на полные резервы времени t 1,2 = 13, t 3,5 = 13. Очевидно, что одновременное увеличение продолжительности работ (1,2) и (3,5) целесообразнее увеличения продолжительности работы (5,7), так как Еще раз подчеркнем, что данная задача решалась при условии, когда продолжительность работ директивно не ограничивалась. Если сравнить оптимальную продолжительность работ с нормальной (см. табл. 3.6), то нетрудно заметить, что для трех работ из четырех установлена продолжительность, превышающая нормальную: t 3,6 >10, t 1,2 >10, t 3,5 >11. Рассмотрим теперь формулировку задачи оптимизации сетевого графика в общем виде. Стоимость выполнения работы (i, j) равна:
Учитывая, что для работ, принадлежащих критическому пути,
Можно выделить известные сроки наступления событий критического пути,
Правые части данных равенств состоят из двух слагаемых, первые из которых содержат известные величины
где
Систему линейных ограничений можно записать в виде
В справедливости полученных выражений нетрудно убедиться путем подстановки в них исходных данных, приведенных в табл. 3.6 и на рис. 3.12. В результате должны быть получены система ограничений (3.1), (3.2) и функция цели (3.3). Теперь рассмотрим оптимизацию сетевого графика по стоимости при условии, что максимальная продолжительность работ ограничена значениями Предположим, что начало работы всегда совпадает со сроком наступления предшествующего события. Для работ, начинающихся событиями критического пути, эти сроки определены, а для остальных работ – находятся в промежутках времени между ранними и поздними сроками наступления соответствующих событий. Обозначим
Продолжительность работ, не принадлежащих критическому пути,
Стоимость выполнения работ определим по формулам:
Суммарная стоимость всего комплекса работ составляет
Выделим в полученном выражении известные сроки начала работ
где Сформулируем задачу оптимизации сетевого графика по стоимости для условий, заданных на рис. 3.12. Ограничения (3.4) – (3.10) справедливы для работ, не принадлежащих критическому пути. Ограничение (3.4) определяет сроки начала работ (1,2), (1,4), (3,5), (3,6); ограничение (3.5) – сроки завершения работ (1,4), (3,6), (5,7); ограничения (3.6) и (3.7) – диапазон сроков начала и завершения работ, инцидентных событиям 2 и 5; ограничение (3.8) отражает условие для событий 2 и 5, согласно которому последующая для данного события работа не может начаться раньше, чем завершатся все работы, ему предшествующие; неравенства (3.9) и (3.10) ограничивают продолжительность работ в пределах от минимальной до нормальной. Следовательно, систему линейных ограничений можно записать в таком виде:
Подставив численные значения временных параметров, указанные на рис. 3.12 и в табл. 3.6, и исключив избыточные ограничения, получим
Определим функцию цели
Подчеркнем, что размерность данной задачи линейного программирования значительно больше размерности задачи без ограничений максимальной продолжительности работ. В некоторых случаях, учитывая конкретную структуру сетевого графика, размерность задачи можно уменьшить. Так, в рассматриваемом примере можно определить оптимальную продолжительность работ (1,4) и (3,6), поскольку она помещена между критическими событиями. Для работы (1,4) резерв времени меньше разности В результате решения задачи оптимизации сетевого графика по стоимости получим:
Рассчитанным срокам начала и окончания работ соответствует следующая их продолжительность:
В заключение отметим, что если на сетевом графике нельзя выделить путь или фрагмент пути с нормальной продолжительностью работ, имеющих резерв времени, то соответствующие работы можно не рассматривать при построении оптимизационной модели, приняв их продолжительность равной максимально возможному значению.
3.9. Практические задания I. По приведённым ниже данным построить сетевую модель, упорядо- чить её, определить временные параметры событий и работ. Найдите критическое время завершения всего комплекса работ и выделите критический путь: 1)
2)
3)
4)
5) 6) 7) 8) 9) II. По данным нижеприведенной таблицы построить сетевой график, про- извести оптимизацию продолжительности работ сетевого графика, т.е. сократить критический путь до директивной величины при минимальном увеличении стоимости всего комплекса работ (где k – это последняя цифра шифра зачётной книжки студента).
III. Проект представлен сетевым графиком:
Для каждой работы известны её нормальная продолжительность tнij (первое число на графике) и минимально возможное время выполнения tmij (второе число). Задан срок выполнения проекта t 0 = 20. Δ C 12 = 1; Δ C 13 = 5; Δ C 23 = 1; Δ C 24 = 3; Δ C 35 = 2; Δ C 45 = 5. Требуется сократить критический путь до t 0 так, чтобы суммарное количество используемых средств было минимальным, продолжительность выполнения каждой работы была не меньше заданной величины tmij.
Вопросы для самоконтроля к главе 3: 1. В каких случаях прибегают к составлению сетевого графика? 2. Что показывает полный резерв времени пути? 3. Сколько существует разновидностей резервов времени работ? Перечислите их. 4. По какой формуле рассчитывается резерв времени события? 5. Назовите основные правила построения сетевой модели. 6. Что представляет собой сетевая модель? 7. Назовите основные элементы сетевого графика. 8. Как определить критический путь?
Заключение В данном учебном пособии раскрыта сущность и формы системных исследований. Изложены основные понятия и принципы системного подхода. Раскрыта сущность системного анализа как прикладного аспекта системного подхода. Перечислены основные методы системного анализа. Так как системный анализ имеет прикладной характер и одним из основных этапов его применения выступает процесс моделирования, то уместным было отразить применение системного подхода в процессе управления экономическими объектами. В третьей части пособия изложены элементы теории сетевого планирования. Сетевое планирование наиболее наглядно позволяет представить любой целостный процесс в виде частей системы: событий и работ. Этот метод широко применяется в исследовании проблем организации крупномасштабных мероприятий, а именно решением таких задач занимается системный анализ. Удобство зрительного восприятия, возможность выявить главное, относительная простота вычислений делают метод сетевого планирования пригодным для анализа систем различной природы. В пособии даны понятия и определения основных элементов сетевой модели. Перечислены основные принципы построения сетевого графика (модели). Показаны способы оптимизации сетевых графиков.
В учебном пособии достаточно подробно и доходчиво изложен алгоритм построения и расчёта сетевой модели, а также её анализ и оптимизация.
Список литературы 1. Багриновский К.А., Сумин Г.А. Модели и методы прогнозирования и долгосрочного планирования народного хозяйства. – М.: Изд-во РУДН, 1993. 2. Багриновский К.А., Рубцов В.Н. Модели и методы прогнозирования и долгосрочного планирования народного хозяйства. – М.: Изд-во РУДН, 1992. 3. Вентцель Е.С. Исследование операций: Задачи, принципы, методология. – М.: Наука, 1980. 4. Карасёв А.И., Кремер Н.Ш., Савельев Т.И. Математические методы и модели в планировании. – М.: Экономика, 1987 5. Кобелев Н.Б. Методы оптимального управления отраслью обслуживания населения.– М.: Изд-во лег. пищ. пром., 1981. 6. Радченко А.И. Основы государственного и муниципального управления: системный подход: учебник. Ростов н/Д: АООТ «Ростиздат»,. 1997. 7. Резниченко С.С. Математическое моделирование в горной промышленности. – М.: Недра, 1987.
Учебное издание
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.209.98 (0.087 с.) |
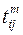 , стоимость выполнения (при этой продолжительности)
, стоимость выполнения (при этой продолжительности)  и коэффициент стоимости
и коэффициент стоимости 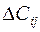 (табл. 3.6). Приведенная в таблице нормальная продолжительность работ на этом этапе не принимается во внимание, поскольку в данной постановке задачи продолжительность работ не ограничена.
(табл. 3.6). Приведенная в таблице нормальная продолжительность работ на этом этапе не принимается во внимание, поскольку в данной постановке задачи продолжительность работ не ограничена.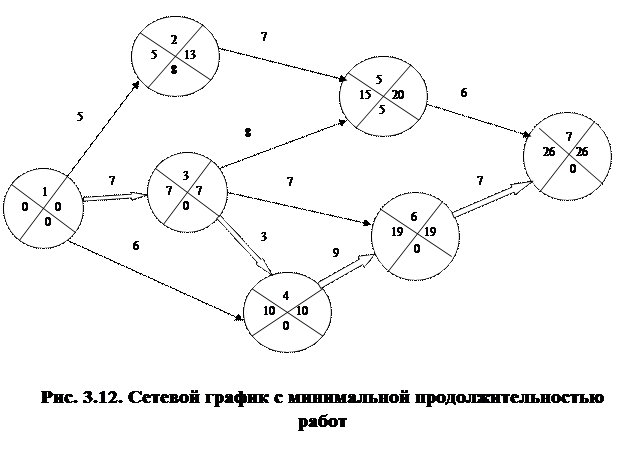
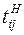
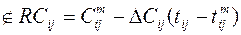 , где tij – искомая продолжительность работы (i,j).
, где tij – искомая продолжительность работы (i,j).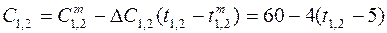 ;
;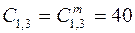 ;
; ;
;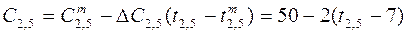 ;
;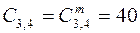 ;
; ;
;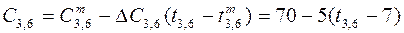 ;
;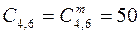 ;
;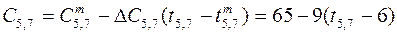 ;
; .
.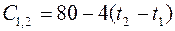 ;
; 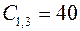 ;
;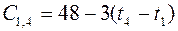 ;
; 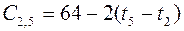 ;
;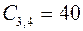 ;
; 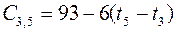 ;
;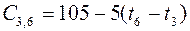 ;
; 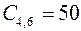 ;
; ;
; 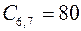 .
.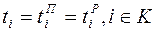 , следовательно, согласно рис. 3.12, имеем t 1 = 0, t 3 = 7, t 4 = 10, t 6 = 19, t 7 = 26. Для событий, не принадлежащих критическому пути, получим 5 ≤ t 2 ≤ 13, 15 ≤ t 5 ≤ 20. Таким образом, неизвестными являются только моменты времени наступления событий, не принадлежащих критическому пути (для остальных событий моменты их наступления определены).
, следовательно, согласно рис. 3.12, имеем t 1 = 0, t 3 = 7, t 4 = 10, t 6 = 19, t 7 = 26. Для событий, не принадлежащих критическому пути, получим 5 ≤ t 2 ≤ 13, 15 ≤ t 5 ≤ 20. Таким образом, неизвестными являются только моменты времени наступления событий, не принадлежащих критическому пути (для остальных событий моменты их наступления определены).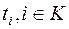 , в результате получим:
, в результате получим: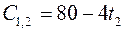 ;
; 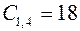 ;
; 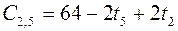 ;
;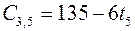 ;
; 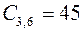 ;
;  ;
; 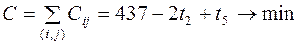 . (3.1)
. (3.1)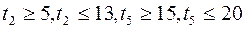 (3.2)
(3.2)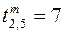 . Поскольку это недопустимо, необходимо учесть еще одно ограничение t 5 – t 2 ≥ 7. (3.3)
. Поскольку это недопустимо, необходимо учесть еще одно ограничение t 5 – t 2 ≥ 7. (3.3)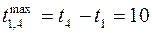 ,
, 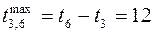 .
.
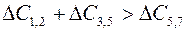 ; эти работы в результате продлеваются на 5 единиц времени (полный резерв времени работы (3,5)). После этого работа (5,7) лишается резерва времени и остается на уровне минимальной продолжительности
; эти работы в результате продлеваются на 5 единиц времени (полный резерв времени работы (3,5)). После этого работа (5,7) лишается резерва времени и остается на уровне минимальной продолжительности 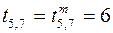 . У работ (1,2) и (2,5) остается резерв времени 3 единицы, который следует отдать работе (1,2), поскольку
. У работ (1,2) и (2,5) остается резерв времени 3 единицы, который следует отдать работе (1,2), поскольку 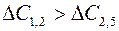 . Следовательно, работа (2,5) сохраняет минимальную продолжительность
. Следовательно, работа (2,5) сохраняет минимальную продолжительность 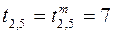 .
.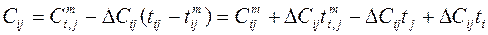 .
.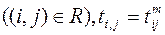 , суммарную стоимость выполнения всего комплекса работ можно записать в виде
, суммарную стоимость выполнения всего комплекса работ можно записать в виде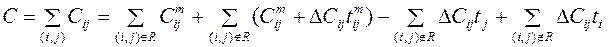 .
. . Из такого разделения множества событий на два подмножества получим:
. Из такого разделения множества событий на два подмножества получим: ,
,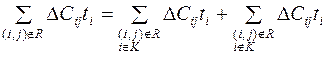 .
. ,
,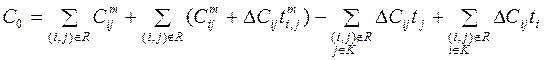 .
.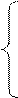
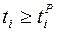 ;
;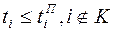 ;
;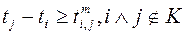 .
.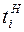 (см. табл. 3.6). В этом случае для работ, заканчивающихся событиями критического пути, моменты времени их завершения могут не совпадать со сроками наступления соответствующих событий (например, работы (1,4) и (3,6) на рис. 3.12). Аналогично, сроки наступления некритических событий могут не совпадать со сроками завершения некоторых из входящих в них работ.
(см. табл. 3.6). В этом случае для работ, заканчивающихся событиями критического пути, моменты времени их завершения могут не совпадать со сроками наступления соответствующих событий (например, работы (1,4) и (3,6) на рис. 3.12). Аналогично, сроки наступления некритических событий могут не совпадать со сроками завершения некоторых из входящих в них работ.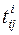 и
и 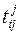 – момент времени соответственно начала и завершения работы (i,j). Очевидно, что для работ критического пути
– момент времени соответственно начала и завершения работы (i,j). Очевидно, что для работ критического пути 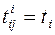 ,
, 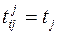 ,
, 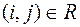 ; для работ, начинающихся событиями критического пути,
; для работ, начинающихся событиями критического пути, 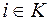 ; для работ, завершающихся событиями критического пути,
; для работ, завершающихся событиями критического пути, 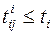 ,
, 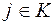 ,
, 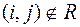 .
. должна находиться в пределах между минимальной и нормальной продолжительностью. Учитывая, что сроки наступления событий критического пути определены при построении исходного сетевого графика, для искомых моментов времени начала и завершения работ
должна находиться в пределах между минимальной и нормальной продолжительностью. Учитывая, что сроки наступления событий критического пути определены при построении исходного сетевого графика, для искомых моментов времени начала и завершения работ 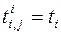 ,
, 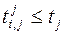 ,
, 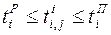 ,
,  ; (3.6)
; (3.6)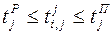 ,
, 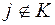 ; (3.7)
; (3.7)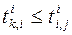 ,
, 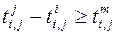 ; (3.9)
; (3.9)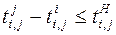 ; (3.10)
; (3.10)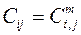 ,
, 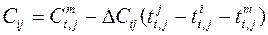 ,
, 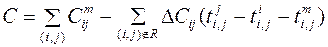 .
.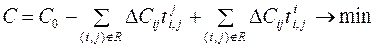 ; (3.11)
; (3.11)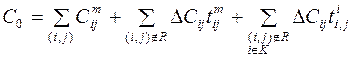 .
.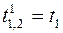 ,
, 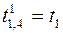 ,
, 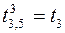 ,
, 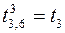 ;
; 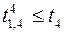 ,
, 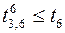 ,
, 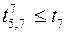 ,
, 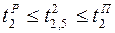 ;
; 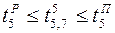 ;
; 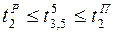 ;
; 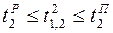 ;
; 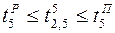 ;
; 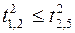 ;
; 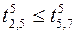 ;
; 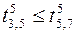 ;
;  ;
; 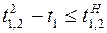 ;
; 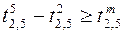 ,
, 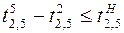 ;
; 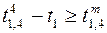 ,
,  ;
; 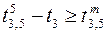 ,
, 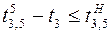 ;
; 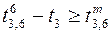 ,
,  ;
; 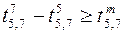 ,
,  .
.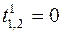 ,
, 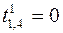 ,
, 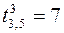 ,
, 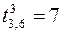 ;
; 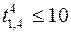 ,
,  ,
,  ;
;  ;
; 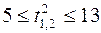 ;
; 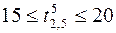 ;
; 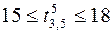
 ,
,  ;
; 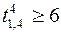 ,
,  ,
,  ;
;  ,
, 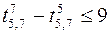 .
.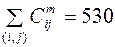 ;
;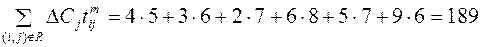 ;
; ;
; ;
;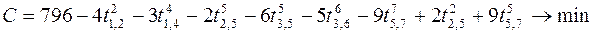 .
. , поэтому
, поэтому 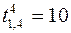 , для работы (3,6) резерв времени больше разности
, для работы (3,6) резерв времени больше разности 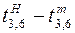 , таким образом
, таким образом 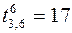 .
.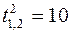 ,
, 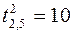 ,
, 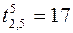 ,
, 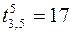 ,
, 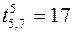 ,
, 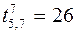 .
.
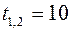 ,
, 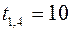 ,
, 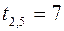 ,
, 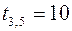 ,
,  ,
,  .
.