
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерій узгодженості Колмогорова-СмирноваСтр 1 из 3Следующая ⇒ Вступ Математична статистика вивчає способи отримання статистичних закономірностей на підставі спостережень випадкових величин. Статистичною гіпотезою називається будь-яке твердження про вигляд або властивості розподілу спостережуваних в експерименті випадкових величин (зазвичай вона позначається Перевірка статистичної гіпотези полягає в тому, щоб сформулювати таке правило, яке дозволило б за результатами відповідних спостережень прийняти або відхилити гіпотезу. Рішення статистичних задач зазвичай містить два етапи: припущення про розподіл досліджуваної випадкової величини і вивчення цієї величини в рамках зробленого припущення. При цьому, природно, необхідно встановити, наскільки припущення про розподіл випадкових величин відповідають експериментальним даним. Прийнято ставити питання у формі: чи не вступає прийнята статистична модель в протиріччя з наявними даними. Критерії, що вирішують таке завдання, називають критеріями згоди. Критеріями згоди називають статистичні критерії, призначені для виявлення розбіжностей між гіпотетичною статистичною моделлю і реальними даними, які ця модель покликана описати. Вважаємо, що спостереження становлять випадкову вибірку, а теоретична модель описує закон розподілу ймовірностей, який управляє випадковим вибором. Важливо, що цей розподіл має бути вибрано незалежно від тих даних, за якими будемо його перевіряти. Інакше кажучи, неприпустимо спочатку "підігнати" по вибірці деякий закон розподілу, а потім намагатися перевірити згоду з отриманим законом по цій же вибірці. Допускається розбити вибірку на дві частини, по одній "підігнати" закон розподілу, а по інший - перевірити його. Говорячи по теоретичному законі розподілу, якому гіпотетично мали б слідувати елементи даної вибірки, треба розрізняти прості і складні гіпотези про цей закон: • проста гіпотеза прямо вказує якийсь певний закон ймовірностей (розподіл ймовірностей), по якому виникли вибіркові значення; • складна гіпотеза вказує на єдиний розподіл (наприклад, параметричне сімейство). Критерії згоди засновані на використанні різних заходів відстаней між аналізованим емпіричним розподілом і функцією розподілу ознаки у генеральній сукупності.
Перевірка гіпотез про узгодженність Застосовуючи критерії узгодженості для перевірки відповідності спостережуваного відомого розподілу теоретичному закону, слід розрізняти перевірку простих і складних гіпотез. Проста перевіряюча гіпотеза має вигляд H0: F (x) = F (x, θ), де F (x, θ) - функція розподілу ймовірностей, з якої перевіряють узгодженість спостережуваної вибірки, а θ - відоме значення параметра (скалярного або векторного). Складна перевіряюча гіпотеза має вигляд H0: F (x) Î {F (x, θ), θ Î У процесі перевірки узгодженості по вибірці обчислюють значення S* статистики використовуваного критерію. Потім для того, щоб зробити висновок про прийняття або відхилення гіпотези Н0, необхідно знати умовний розподіл G (S ½ Н0) статистики S при справедливості Н0. У процесі перевірки узгодженості по вибірці обчислюють значення S* статистики використовуваного критерію. Потім для того, щоб зробити висновок про прийняття або відхилення гіпотези Н0, необхідно знати умовний розподіл G (S ½ Н0) статистики S при справедливості Н0. І якщо ймовірність P досить велика, принаймні P {S Перевірка простої гіпотези При перевірці узгодженосі відомого розподілу з теоретичним розподілом випадкової величини Х діють наступним чином. а) Формулюють перевіряючу гіпотезу, вибираючи теоретичний розподіл випадкової величини, узгодженність якого з досвідченим розподілом цієї величини слід перевірити; б) Із сукупності відбирають випадкову вибірку обсягу n. Отримані результати спостережень розташовують у порядку їх зростання, так, що у розпорядженні мають впорядковану вибірку значень x1 ≤ х2 ≤... ≤ хn ; в) У відповідності з обраним критерієм перевірки обчислюють значення статистики S* критерію (за формулою Sk = г) У відповідності з обраним критерієм перевірки обчислюють значення P де G (s ½ H 0) - розподіл статистики критерію при справедливості гіпотези H0. Якщо P {S> S*} > α, де α - рівень значимості, то немає підстав для відхилення перевіряючої гіпотези. В іншому випадку перевіряючу гіпотезу Н0 відкидають. Можна обчислюване значення статистики S* порівняти з критичним значенням Перевірка складної гіпотези При перевірці узгодженості відомого розподілу з теоретичним розподілом випадкової величини X діють наступним чином. а) Формулюють перевіряючу гіпотезу, вибираючи теоретичний розподіл F(х, θ) випадкової величини, узгодженість якого з відомим розподілом цієї величини слід перевірити. б) Із сукупності відбирають випадкову вибірку обсягу n. Отримані результати спостережень розташовують у порядку їх зростання, так, що у розпорядженні мають впорядковану вибірку значень в) У відповідності з обраним критерієм перевірки, теоретичним розподілом F (x, θ) визначають розподіл статистики критерію G (S ½ H0) при справедливості гіпотези H0. г) Обчислюють значення P ж) Якщо P{S > S*} > α, де α - рівень значимості, то немає підстав для відхилення перевіряючої гіпотези. В іншому випадку перевіряюча гіпотеза H0 відкидається. Можна обчислене значення статистики S* порівняти з критичним значенням Sα, обумовленим з умови Приклади 1. Перевірити гіпотезу про однорідність двох вибірок.
Розв’язок: Так як вибірка є незгрупованою, то для перевірки гіпотези однорідності вибірок X і Y можна скористатися критерієм однорідності Смирнова. Задамо рівень значущості Статистика критерію однорідності Смирнова:
2. Перевірити просту гіпотезу про приналежність вибірки експоненціальному закону. Впорядкована вибірка обсягом 100 спостережень має вигляд:
Розв’язок: Перевіряюча гіпотеза має вигляд Н0 : А) Критерій Колмогорова. Значення статистики розраховують за формулою Sk = Б) Критерій Смирнова. Значення статистики розраховують за формулою Sm = Як бачимо, при заданні рівня значущості α <0,2548 (для критерію Смирнова), немає підстав для відхилення перевіряючої гіпотези за критеріями згоди.
3. Перевірити складну гіпотезу про приналежність вибірки з прикладу 2 експоненціальному закону Перевіряюча гіпотеза має вигляд Н0 : А) Критерій Колмогорова. Значення статистики розраховують за формулою Sk = Б) Критерій Смирнова. Значення статистики розраховують за формулою Sm = По критеріям згоди вибірки з експонентним законом досить задовільні.
Висновок В даній курсовій роботі мною було розглянуто один з непараметричних критеріїв,оснований на аналізі емпіричного розподілу і функції розподілу в генеральній сукупності, а саме критерій Колмогорова-Смирнова,який застосовується в математичній статистиці з метою перевірки простих і складних гіпотез. Було розглянуто відмінність окремо критерію Колмогорова та окремо критерію Смирнова. На основі теоретичної частини я розглянула декілька практичних моментів з застосуванням приведених вище алгоритмів кожного з параметрів. Вступ Математична статистика вивчає способи отримання статистичних закономірностей на підставі спостережень випадкових величин. Статистичною гіпотезою називається будь-яке твердження про вигляд або властивості розподілу спостережуваних в експерименті випадкових величин (зазвичай вона позначається Перевірка статистичної гіпотези полягає в тому, щоб сформулювати таке правило, яке дозволило б за результатами відповідних спостережень прийняти або відхилити гіпотезу. Рішення статистичних задач зазвичай містить два етапи: припущення про розподіл досліджуваної випадкової величини і вивчення цієї величини в рамках зробленого припущення. При цьому, природно, необхідно встановити, наскільки припущення про розподіл випадкових величин відповідають експериментальним даним. Прийнято ставити питання у формі: чи не вступає прийнята статистична модель в протиріччя з наявними даними. Критерії, що вирішують таке завдання, називають критеріями згоди. Критеріями згоди називають статистичні критерії, призначені для виявлення розбіжностей між гіпотетичною статистичною моделлю і реальними даними, які ця модель покликана описати. Вважаємо, що спостереження становлять випадкову вибірку, а теоретична модель описує закон розподілу ймовірностей, який управляє випадковим вибором. Важливо, що цей розподіл має бути вибрано незалежно від тих даних, за якими будемо його перевіряти. Інакше кажучи, неприпустимо спочатку "підігнати" по вибірці деякий закон розподілу, а потім намагатися перевірити згоду з отриманим законом по цій же вибірці. Допускається розбити вибірку на дві частини, по одній "підігнати" закон розподілу, а по інший - перевірити його. Говорячи по теоретичному законі розподілу, якому гіпотетично мали б слідувати елементи даної вибірки, треба розрізняти прості і складні гіпотези про цей закон: • проста гіпотеза прямо вказує якийсь певний закон ймовірностей (розподіл ймовірностей), по якому виникли вибіркові значення; • складна гіпотеза вказує на єдиний розподіл (наприклад, параметричне сімейство). Критерії згоди засновані на використанні різних заходів відстаней між аналізованим емпіричним розподілом і функцією розподілу ознаки у генеральній сукупності.
Критерій узгодженості Колмогорова-Смирнова Критерій узгодженості Колмогорова-Смирнова застосовується для перевірки гіпотез лише про неперервні закони розподілу: неперервна випадкова величина Х має рівномірний розподіл на відрізку [a, b], якщо на цьому відрізку щільність розподілу ймовірності випадкової величини постійна, тобто якщо диференціальна функція розподілу f (х) має наступний вигляд:
Даний критерій дозволяє проводити перевірку узгодженості емпіричної функції розподілу з теоретичною. Перевіряється справедливість гіпотези H0: F*(x) = F(x) в протиставлення гіпотезі H1: F*(x) ≠ F(x). Критерій узгодженості Колмогорова заснований на тому факті, що розподіл супремума різниці між теоретичною і емпіричною функціями розподілу Dn = sup │F*(x) – F(x)│ однаковий для будь-якої F(x). Величину Dn називають статистикою Колмогорова. При малих n для статистики Колмогорова є таблиці критичних точок Dкр. При великих n використовують граничний розподіл Колмогорова: P( Для розподілу Колмогорова, граничного для статистики У загальному випадку функція розподілу F(x) може бути і різною, хоча вона має розриви тільки першого роду, які є скачками. Тому вибіркову статистику
при цьому
Алгоритм перевірки гіпотези: 1. Результати спостереження представляються у вигляді інтервального статистичного ряду. 2. Знаходиться значення емпіричної функції розподілу F*(x). 3. Користуючись гіпотетичною функцією розподілу, обчислюють значення F(x) теоретичної функції розподілу, що відповідають спостережуваним значенням випадкової величини 4. Знаходять Dn і розраховують спостережуване значення вибіркової статистики 5. За заданимм рівнем значущості 6. Порівнюючи спостережуване значення вибіркової статистики а) якщо Dn б) якщо Dn Примітка. Критерій Колмогорова, строго говорячи, не можна застосовувати у випадках згрупованних даних при невідомих параметрах розподілу. Тим не менш, він інколи застосовується на практиці і в подібних випадках. Однак, при цьому статистики критерію виходять заниженими, що збільшує помилку першого роду. Тоді слід використовувати інші критерії.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.132 (0.004 с.) |
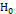 і називається основною).
і називається основною).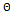 }, де
}, де  - область визначення параметра θ. У цьому випадку оцінку параметра розподілу обчислюють за тією ж самою вибіркою, за якою перевіряють згоду. Якщо оцінку обчислюють за іншою вибіркою, то гіпотеза проста.
- область визначення параметра θ. У цьому випадку оцінку параметра розподілу обчислюють за тією ж самою вибіркою, за якою перевіряють згоду. Якщо оцінку обчислюють за іншою вибіркою, то гіпотеза проста.
 S*}
S*}  (s ½ Н0) - умовна щільність, а α - рівень значущості (ймовірність помилки 1-го роду - відхилити справедливу гіпотезу Н0), то прийнято вважати, що немає підстав для відхилення гіпотези Н0.
(s ½ Н0) - умовна щільність, а α - рівень значущості (ймовірність помилки 1-го роду - відхилити справедливу гіпотезу Н0), то прийнято вважати, що немає підстав для відхилення гіпотези Н0.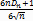 );
); ,
, , що визначається з умови
, що визначається з умови  . Гіпотезу про узгодженість відкидають, якщо значення статистики потрапляє в критичну область, тобто при S* >
. Гіпотезу про узгодженість відкидають, якщо значення статистики потрапляє в критичну область, тобто при S* >  .
.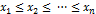 .
.
 .
. . Гіпотезу про узгодженість не відкидають, якщо S* < Sα.
. Гіпотезу про узгодженість не відкидають, якщо S* < Sα.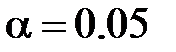 .
. , де
, де 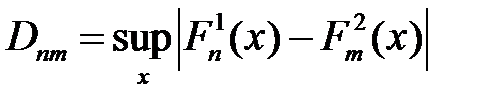 підпорядковується розподілу Колмогорова
підпорядковується розподілу Колмогорова 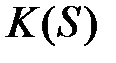 .
. 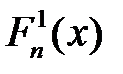 – емпірична функція розподілу по першій вибірці,
– емпірична функція розподілу по першій вибірці, 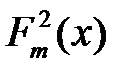 – по другій. Проводячи обчислення, отримуєм:
– по другій. Проводячи обчислення, отримуєм:  ,
,  ,
, 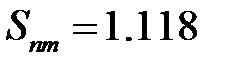 . Знаходимо за табличкою критичне значення статистики Смирнова при
. Знаходимо за табличкою критичне значення статистики Смирнова при 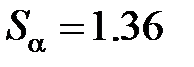 . Оскільки
. Оскільки  , то нема підстав для відхилення гипотези про однородності вибірок X и Y.
, то нема підстав для відхилення гипотези про однородності вибірок X и Y. 0.1
0.1
 при
при 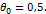
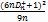 : S *m = 2,7349. При цьому значенні статистики обчислюють ймовірність P { S m >S* m} =
: S *m = 2,7349. При цьому значенні статистики обчислюють ймовірність P { S m >S* m} = 
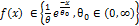 при
при 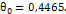
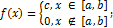

 , також існують таблиці критичних точок
, також існують таблиці критичних точок  . Практично їх використовують вже при n> 20.
. Практично їх використовують вже при n> 20. в загальному випадку визначають за допомогою точної верхньої межі (sup):
в загальному випадку визначають за допомогою точної верхньої межі (sup): ,
, 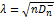 - статистика Смирнова,
- статистика Смирнова, ,
,  - статистика Колмогорова,
- статистика Колмогорова, .
. .
.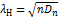 .
. із таблиць квантилей розподілу Колмогорова знаходять критичні точки
із таблиць квантилей розподілу Колмогорова знаходять критичні точки 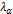 .
.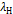 з критичною точкою
з критичною точкою 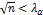 , то вважається, що для відхилення нульової гіпотези підстав нема, тобто, гіпотетична функція розподілу узгоджується з досвідченими даними;
, то вважається, що для відхилення нульової гіпотези підстав нема, тобто, гіпотетична функція розподілу узгоджується з досвідченими даними;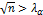 , то нульова гіпотеза відхиляється на користь альтернативної.
, то нульова гіпотеза відхиляється на користь альтернативної.


