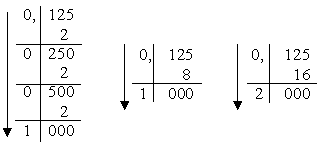Непозиційній системи числення

Непозиційна система числення – система числення, в якій значення кожної цифри в довільному місці послідовності цифр, яка означає запис числа, не змінюється.

У непозиційній системі кожен знак у запису незалежно від місця означає одне й те саме число. Добре відомим прикладом непозиційної системи числення є римська система, в якій роль цифр відіграють букви алфавіту: І – один, V – п'ять, Х – десять, С – сто, L – п'ятдесят, D – п'ятсот, М – тисяча. Наприклад, 324 = СССХХІV. У непозиційній системі числення незручно й складно виконувати арифметичні операції.

Недоліками непозиційних систем числення є:

громіздкість зображення чисел;

труднощі у виконанні операцій.

 

Римська цифра	Десяткове значення
I
V
X
L
C
D
M

 

Позиційній системи числення

Позиційна система числення – система числення, в якій значення кожної цифри залежить від місця в послідовності цифр у записі числа. Для позиційних систем числення характерні наочність зображення чисел і відносна простота виконання операцій.

У позиційних системах числення одна і та ж цифра (числовий знак) у записі числа набуває різних значень залежно від своєї позиції. Таким чином, позиція цифри має вагу у числі. Здебільшого вага кожної позиції кратна деякому натуральному числу b (b >1), яке називається основою системи числення.

Основа системи числення – число, яке означає, у скільки разів одиниця наступного розрядку більше за одиницю попереднього.

Винахід позиційної системи числення, заснованої на помісному значенні цифр, приписують шумерам і вавилонцям. Її було розвинуто індусами і вона отримала неоціненні наслідки для історії людської цивілізації.

Для запису чисел системи числення з основою до 36 включно у якості цифр використовуються арабські цифри (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) а потім букви латинського алфавіту (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z). При цьому, a = 10, b = 11 і т.д.

 

Загальноприйнятою в сучасному світі є десяткова позиційна система числення, яка з Індії через арабські країни прийшла в Європу. Араби взяли за основу число 10, тому що в якості обчислювального пристрою вони використовували 10 пальців рук. В десятковій системі для запису числа використовується десять цифр від 0 до 9 і основою є число 10. Число у цій системі числення можна представити у вигляді степенів десяти, наприклад:

237₁₀ = 2·10²+3·10¹ + 7·10⁰

130678₁₀ = 1*10⁵ + 3*10⁴ + 0*10³ + 6*10² + 7*10¹ + 8*10⁰

Тут 10 є основою системи числення, а показник степеня – це номер позиції цифри в записі числа (нумерація ведеться зліва на право, починаючи з нуля). Арифметичні операції у цій системі виконують за правилами, запропонованими ще в середньовіччі. Наприклад, додаючи два багатозначних числа, застосовуємо правило додавання стовпчиком. При цьому все зводиться до додавання однозначних чисел, для яких необхідним є знання таблиці додавання.

 

Також поширені системи числення з основами:

2 – двійкова (у дискретній математиці, інформатиці, програмуванні)

8 – вісімкова (у програмуванні)

12 – дванадцятирічна (мала широке застосування у давнину, подекуди використовується і нині)

16 – шістнадцятирічна (поширена у програмуванні, а також для кодування шрифтів)

60 – шістдесяткова (для виміру кутів і, зокрема, довготи і широти)

 

Питання9

Форми представлення чисел. Форма з фіксованою крапкою.

В сучасних ЕОМ застосовуються два способу представлення чисел: з ф³ксованою крапкою ³плаваючою крапкою.

В першому випадку м³сце коми, яка в³дд³ляº ц³лу частину числа в³д дробово¿, визначаºться на етап³конструювання ЕОМ. Зразу ж вказуºться к³льк³сть розряд³в, як³ в³дводяться для зображення ц³ло¿ ³дробово¿ частин. Причому кожному розряду ком³рки в³дпов³даº завжди один ³ той же розряд числа, що суттºво спрощуº виконання арифметичних д³й.

Нехай, наприклад, ком³рка пам’ят³ машини маº 24 дв³йкових розряда. Як ми знаºмо, в ком³рку можна записати будь-яке машинне слово, тобто дов³льний наб³р з нулів ³ одиниць. Якщо це слово - число, то в конструкц³¿ машини може бути передбачено його представлення в форм³ з ф³ксованою комою. Наприклад, воно може бути таким: крайн³й зл³ва розряд - знаковий, пот³м наступні 9 розряд³в в³дводяться п³д ц³лу частину ³, накінець, 14 розряд³в, як³ залишилися, п³д дробову частину числа, тобто кома тут завжди на одному ³ тому ж м³сц³ - п³сля десятого розряду машинного слова (з врахуванням знакового розряду). Тод³ найб³льше число, яке можна представити, буде: (111111111,11111111111111) _2.

Видно, що воно менше, н³ж 2⁹ = (512) ₁₀. А найменше за модулем в³дм³нне в³д нуля число дор³внюº

(000000000,00000000000001) ₂ = 2^-14.

Тобто, д³апазон чисел, як³ можна записати в ком³рку пам’т³ машини, тут такий:

2^-14 < |a| < 2⁹.

Форма з плаваючою крапкою.

Для того, щоб зб³льшити д³апазон чисел, використовують другу форму запису чисел - з плаваючою комою. Будь-яке число в систем³ числення з основою Q можна записати так:

a=A*Q^p.

A називають мантисою числа, а P - порядком.

Наприклад, в десятков³й систем³ числення число 3,14 представимо у вигляд³

3,14 = 0,314*10¹.

Тут мантиса дор³внюº 0,314, а порядок 1. Очевидно, таке представлення далеко не однозначне. Число 3,14 записати так:

3,14=3,14*10⁰ = 31,4*10^-1 = 0,0314*10² =...

Порядок числа визначаº положення коми в запису мантиси. При коректуванн³ порядку в³дпов³дним чином зм³нюºться ³ положення коми - кома ніби ”плаваº".

Зв³дси ³ назва методу представлення чисел. З плаваючою комою число, як ми т³льки що бачили, представляºться неоднозначно. Одне з цих представлень називають нормал³зованим.

В цьому випадку мантиса повинна задов³льняти вимоз³ 1/10 <|А|< 1 (мова йде про десяткову систему числення). Iншими словами, перша цифра мантиси п³сля коми повинна бути в³дм³нною в³д нуля.

9. Представлення довільного числа в формі з плаваючою крапкою. Мантиса та порядок числа. Нормалізована форма представлення числа.

Питання10

Форми представлення чисел. Форма з плаваючою крапкою.

Для того, щоб зб³льшити д³апазон чисел, використовують другу форму запису чисел - з плаваючою комою. Будь-яке число в систем³ числення з основою Q можна записати так:

a=A*Q^p.

A називають мантисою числа, а P - порядком. Наприклад, в десятков³й систем³ числення число 3,14 представимо у вигляд³

3,14 = 0,314*10¹.

Тут мантиса дор³внюº 0,314, а порядок 1. Очевидно, таке представлення далеко не однозначне. Число 3,14 записати так:

3,14=3,14*10⁰ = 31,4*10^-1 = 0,0314*10² =...

Порядок числа визначаº положення коми в запису мантиси. При коректуванн³ порядку в³дпов³дним чином зм³нюºться ³ положення коми - кома ніби ”плаваº". Зв³дси ³ назва методу представлення чисел. З плаваючою комою число, як ми т³льки що бачили, представляºться неоднозначно. Одне з цих представлень називають нормал³зованим. В цьому випадку мантиса повинна задов³льняти вимоз³ 1/10 <|А|< 1 (мова йде про десяткову систему числення). Iншими словами, перша цифра мантиси п³сля коми повинна бути в³дм³нною в³д нуля. В нашому приклад³ десяткове число а=3,14 в нормал³зован³й форм³ маº вигляд 3,14=0,314*10¹.

 

Запишемо кілька чисел в двійковій системі числення в нормалізованій формі:

(7) ₁₀ = (111) ₂ = 111*2⁰ = 111*10⁰ = 0,111*2³ = 0,111*10¹¹

(-9,5) ₁₀ = (-1001,1) ₂ = - 0,10011*2⁴ = - 0,10011*10¹⁰⁰.

Нехай для представлення чисел з плаваючою комою в нас відведено 24 розряди. Нехай один розряд відведено для знаку числа, а другий для знаку порядку:

0 1 2 3 4 5 6 7 8 9 10 11 23

Знак числа| | Порядок Мантиса

Додатнº число, максимальне з можливих в пам’ят³ ЕОМ:

0 1 2 3 4 5 6 7 8 9 10 11 23

Знак числа| | Порядок Мантиса Знак порядку|

М³н³мальне за модулем, в³дм³нне в³д нуля ³ нормал³зоване число

а= (0,1*10^-1111111) ₂ =1/2*2^-127 = 2^-128:

0 1 2 3 4 5 6 7 8 9 10 11 23

Знак числа| | Порядок Мантиса Знак порядку|

В³дм³тимо, що найменше за модулем число, не р³вне нулю ³ не нормал³зоване, яке можна представити в ком³рц³:

а= (1/2) ⁺¹⁵ *2^-127 = 2^-142.

В цьому випадку мантиса

А= (0, 000...01) ₂ = 2^-15, порядок Р = - (1111111) ₂ = - (127) _10.

Питання11

Коди чисел:пряміш, обернений, доповняльний. Модифіковані коди.

В ЕОМ доцільно представляти знаки чисел з допомогою тих же символів через, через які записується саме число. Для цього виділяється додатковий розряд, який називають знаковим і розташовують зліва від старшого розряду числа. Будемо позначати знакові розрядні числа як і відділяти їх крапками від цілої частини числа і комами від дробової.

Для правильності виконання арифметичних операцій над числами, знаки яких закодовані числами, використовують спеціальні способи представлення чисел: прямий, зворотній і додатковий.

Прямий код використовується для вводу-виводу інформації і в запам’ятовуючих пристроях.

Додавання чисел в прямому коді (з одинаковими знаками) не викликає труднощів. Однак додавання чисел з різними знаками в прямих кодах незручно, так як повинно бути спеціальне обладнання для віднімання чисел і визначення знаку різниці.

Операцію алгебраїчного додавання чисел можна звести до операцій додавання при використанні зворотніх і додаткових кодів.

Представлення додатнього числа в зворотньому коді співпадавє з його прямим кодом. Для отримання зворотнього коду від’ємного числа в двійковій системі необхідно в знаковому розряді записати 1, а в інших розрядах одиниці замінити нулями, а нулі одиницями. Аналогічну заміну роблять при перетворенні зворотнього коду від’ємного числа в прямий. На відміну від прямого коду, в зворотньому не можна відкидати нулі після знакового розряду в цілій частині і нулі в кінці дробової частини від’ємного числа.

Представлення додатнього числа в доповнюючому коді співпадавє з його прямим кодом. Правило формування додатнього коду від’ємного числа формулюється так: отримати зворотній код числа і додати 1 в молодший розряд числа. Перетворення доповнюючого коду від’ємного числа здійснюється або зворотнім шляхом (відняти 1 і перетворити в зворотній код) або утворити доповнюючий код до доповнюючого. Нуль, на відміну від прямого і зворотнього кодів, в доповнюючому коді має єдине представлення

Байт - вісім послідовно розміщених бітів, пронумерованих від 0 до 7, при цьому біт 0 є самим молодшим значущим бітом.

Слово - послідовність з двох байтів, які мають послідовну адресу. Розмір слова 16 біт; біти в слові нумеруються від 0 до 15. Байт який містить нульовий біт, називається молодшим байтом, а байт, який містить 15-й біт називають старшим байтом. Мікропроцессори Intel мають важливу особливіть - молодший байт завжди зберігається за молодшою адресою. Адресою слова рахується адреса молодшого байта. Адреса старшого байта може бути використана для доступа до старшої половини слова.

Подвійне слово - послідовність з чотирьох байтів (32 біта), які мають послідовну адресу. Нумерація цих бітів проводиться від 0 до 31. Слово, яке містить нульовий біт називається молодшим словом, а слово яке містить 31-й біт старшим словом. Молодше слово зберігається за меншою адресою. Адресою подвійного слова рахується адреса молодшого слова. Адреса старшого слова може бути використана для доступа до старшої частини подвійного слова..

Чотирьохкратне слово - послідовність з восьми байт (64 біта). які мають послідовну адресу. Номерація цих бітів проводиться від 0 до 63. Слово яке містить нульовий біт називається молодшим подвійним словом словом, а слово яке містить 63-й біт старшим подвійним словом. Молодше подвійне слово зберігається за молодшою адресою. Адресою подвійного слова рахується адреса молодшого слова. Адреса старшого подвійного слова може бути використана для доступа до старшої половини чотирьохкратного слова.

 

Запишемо кілька чисел в двійковій системі числення в нормалізованій формі:

(7) ₁₀ = (111) ₂ = 111*2⁰ = 111*10⁰ = 0,111*2³ = 0,111*10¹¹

(-9,5) ₁₀ = (-1001,1) ₂ = - 0,10011*2⁴ = - 0,10011*10¹⁰⁰.

Нехай для представлення чисел з плаваючою комою в нас відведено 24 розряди. Нехай один розряд відведено для знаку числа, а другий для знаку порядку:

0 1 2 3 4 5 6 7 8 9 10 11 23

Питання 12

Переведення чисел з любої системи числення в десяткову за правилом Полінома.

Переведення цілого числа з десяткової системи числення у будь-яку іншу здійснюється шляхом послідовного ділення числа на основу нової системи числення. Ділення виконується до тих пір, поки остання частка не стане менше дільника. Отримані остачі від ділення, взяті у зворотному порядку, будуть значеннями розрядів числа в новій системі числення. Остання частка дає старшу цифру числа. Приклад: (24)10 = (?)2 (24)10 = (11000)2 Приклад: (143)10 = (?)8 (143)10 = (217)8 Приклад: (687)10 = (?)16 (687)10 = (2AF)16   Для переведення правильного дробу з десяткової системи числення у будь-яку іншу потрібно помножити заданий дріб на основу нової системи числення. Отримана ціла частина добутку буде першою цифрою після коми дробу в новій системі числення. Далі по черзі множаться дробові частини добутків на основу нової системи. Отримані цілі частини добутків будуть цифрами дробу у новій системі числення. Цей процес продовжують до тих пір, поки не буде знайдено число із заданою точністю. Приклад: (0,125)10 = (?)2; (0,125)10 = (?)8; (0,125)10 = (?)16. (0,125)10 = (0,001)2; (0,125)10 = (0,1)8; (0,125)10 = (0,2)16. Приклад: (0,365)10 = (?)16   (0,365)10= (0,5D)16   Для переведення змішаного числа з десяткової системи числення в іншу необхідну окремо перевести цілу й дробову частини за вказаними правилами, а потім об'єднати результати у змішане число.