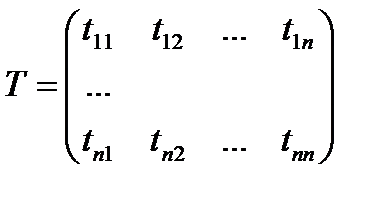Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о связи общих решений неоднородной и однородной систем линейных алгебраических уравнений. ⇐ ПредыдущаяСтр 2 из 2
Общее решение неоднородной системы линейных уравнений имеет вид
, где Х0 – некоторое (частное) решение неоднородной системы уравнений
- общее решение однородной системы AX=B A(X0+C1X1+C2X2+…+ CnXn)=AX0+C1AX1+…+CnAXn=AX0=B
Множество решений неоднородной системы линейных уравнений не образует линейного пространства. 10. Формулы Крамера для системы двух линейных уравнений с двумя переменными.
(Правило Крамера для системы n x n) – Пусть дана система АХ=В из 2 линейных уравнений с 2 неизвестными. То есть у нас получается системы 2х2. Если |А|≠0, то системы имеет единственное решение:
11. Линейная независимость векторов, составляющих ортонормированную систему. Начнем с определения, что такое ортонормированная система.
Здесь доказывается линейная независимость 3х3
Формулы для вычисления координат вектора в ортогональном базисе.
Невырожденность ортогональной матрицы.
14. Изменение матрицы линейного преобразования при замене базиса. А’=T-1AT Пусть А – матрица линейного преобразования f в базисе Предположим, что мы переходим к новому базису, в котором преобразованию отвечает новая матрица А’, а Т есть матрица перехода от исходного базиса к новому базису. Х=ТХ’, где Х – столбец из старых координат разложенного по базису вектора, а Х’ – столбец из новых координат. Аналогично Y=TY’ Учитывая, что Y=AX, Х=ТХ’ и Y=TY’, установим связь между Х’ и Y’. Y’=T-1Y=T-1AX=T-1ATX’ Отсюдаследует, что матрицей отображения А в новом базисе будет матрица A’=T-1ATX, чтд.
Равенство характеристических многочленов подобных матриц. А В: Р-1АР
16. Ортогональность собственных векторов, соответствующих различным собственным значениям самосопряженного линейного преобразования.
Будем вести индукцию по n. В случае n =1 любое преобразование имеет вид Поэтому любой ненулевой вектор х является собственным, и доказывать нечего. Предположим, что утверждение теоремы верно для симметрических преобразований в евклидовом пространстве размерности n-1, и в этом предположении докажем его для евклидова пространства размерности n.
Прежде всего возьмем какое-либо собственное значение λ1 симметрического преобразования f. По теореме о действительности корней уравнения симметрической матрицы λ1 – действительно число. Пусть а 1 – соответствующий собственный вектор.
Обозначим через S – множество всех векторов
Из сказанного следует, что действие f на всем пространстве V можно при желании сузить до действия f на подпространстве S. Применяя предположение индукции, получим, что в S существует ортогональный базис
Изменение матрицы квадратичной формы при замене базиса.
Х=РY
|P|≠0, B=PTAP à =YTBT
20. Выпуклость пересечения выпуклых множеств Доказательство. Пусть М = LÇN, где L, N выпуклы. Пусть АÎM и BÎМ => AÎL и BÎL. L выпуклое => [А,В] Ì L. Пусть АÎM и BÎМ => AÎN и BÎN. N выпуклое => [А,В] Ì N. => [А,В] Ì М => М - выпуклое.
14(411)Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. n – мерное пространство. Vn – базис, состоящий из n векторов.
В пространстве есть базисы Введем матрицу перехода от
Эллипс. Определение. Вывод канонического уравнения.
геометрическое место всех точек плоскости, сумма расстояний от которых до до фокусов есть величина постоянная, большая, чем расстояние между фокусами. Пусть М (х;у) – произвольная точка эллипса. Т.к. MF1 + MF2 = 2a
Т.к. То получаем Или
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.183.1 (0.009 с.) |



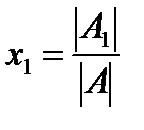
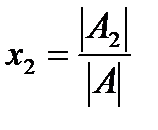 , где А1 означает матрицу, полученную из А заменой 1 столбца столбцом В, а А2 получена из А заменой второго столбца столбцом В.
, где А1 означает матрицу, полученную из А заменой 1 столбца столбцом В, а А2 получена из А заменой второго столбца столбцом В.
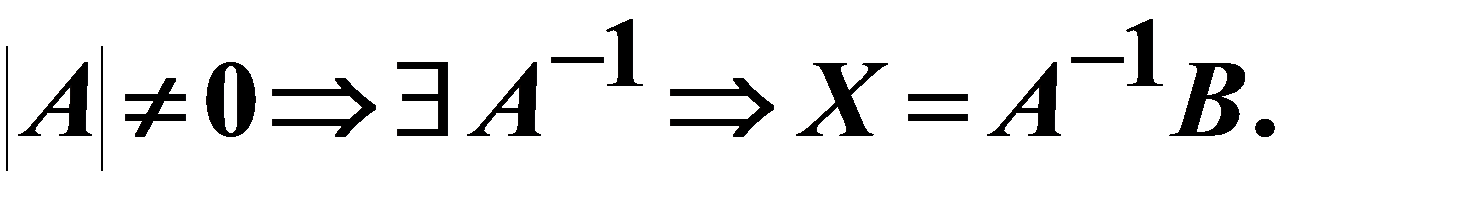



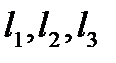 - ортогональный базис
- ортогональный базис

 .
.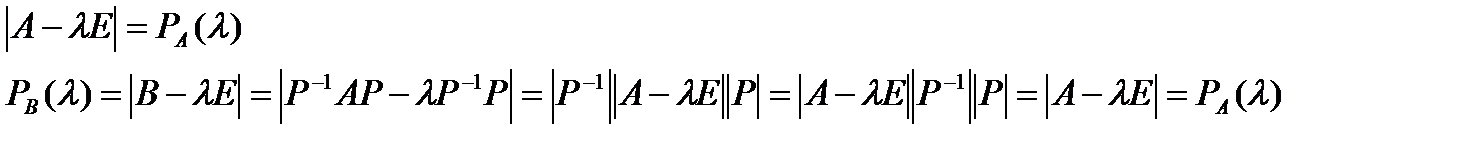
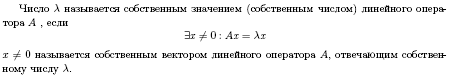


 , ортогональных к а 1
, ортогональных к а 1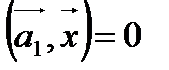 Так как подпространство S есть ортогональное дополнение к линейной оболочке L(а 1), то его размерность равна n-1. Покажем, что это подпространство выдерживает действие f. Это означает, что если
Так как подпространство S есть ортогональное дополнение к линейной оболочке L(а 1), то его размерность равна n-1. Покажем, что это подпространство выдерживает действие f. Это означает, что если  , то
, то 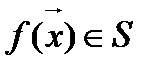 . Действительно,
. Действительно,
 , состоящий из собственных векторов преобразования, т.е.
, состоящий из собственных векторов преобразования, т.е.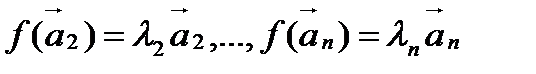
 это доказывает нашу теорему.
это доказывает нашу теорему. , где х – вектор-столбец.
, где х – вектор-столбец.

 к
к 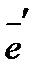 .
.