
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели объектов проектирования
В зависимости от сложности объекта проектирования его моделирование можно проводить на том или ином уровне абстракции. В САПР обычно выделяют три таких уровня: микро, макро и метауровни. Каждый из этих уровней отличается различной степенью детализации рассмотрения процессов, протекающих в объекте проектирования. 6.2.1. Построение модели на микроуровне На микроуровне при описании объекта проектирования фигурируют фазовые переменные, характеризующие физические процессы, протекающие в этом объекте в сплошных средах и непрерывном времени. Примерами таких процессов могут быть поля напряжений и деформации в механических конструкциях, электрические потенциалы в электронных приборах, температура давление в рабочей полости турбины и т.п. Типичными математическими моделями на этом уровне являются системы дифференциальных уравнений в частных производных с заданными краевыми условиями. Краевые условия — это совокупность граничных и начальных условий для исследуемых непрерывных функций. Граничные условия выражают сведения о непрерывных функциях на границах области их определения, а начальные — задают значения этих же функций в начальный момент времени. Примером модели на микроуровне может служить уравнение теплопроводности:
где T — температура тела; l X, l Y — коэффициенты теплопроводности тела по координатам x и y соответственно;
Граничное условие можно задать в виде
Это уравнение показывает, что на границе тела задан поток V теплоты. Одним из наиболее популярных методов решения краевых задач в САПР является метод конечных элементов. Это численный метод, суть которого состоит в разбиении области определения искомой непрерывной функции на отдельные подобласти — конечные элементы. Для каждого элемента выбирается определенное количество узловых точек (узлов) и принимается, что каждый конечный элемент взаимодействует с соседними элементами только в выбранных узлах. В пределах каждого конечного элемента вводится аппроксимирующая функция, которая определяется через значение искомой непрерывной функции в узловых точках. Совокупность аппроксимирующих функций, определенных на множестве конечных элементов, составляет модель искомой непрерывной функции.
Совокупность значений искомой непрерывной функции в узлах, или вектор узловых значений, в общем случае вначале неизвестен. Его определение является наиболее сложной задачей в методе конечных элементов. Алгоритм метода конечных элементов в общем случае состоит из следующих этапов: Этап 1. Разбиение заданной области определения непрерывной функции на некоторое количество конечных элементов Этап 2. Определение для каждого
где
R = (x, y, z) — вектор координат в рассматриваемой точке В зависимости от степени полинома конечные элементы делятся на симплекс–, комплекс– и мультиплекс- элементы. Полиномы симплекс–элементов содержат константы и линейные члены. Полиномы комплекс–элементов содержат также члены более высоких степеней. Полиномы мультиплекс-элементов также содержат члены более высоких степеней, однако границы конечного элемента должны быть параллельны осям координат. Неизвестные вектор–строку коэффициентов полинома В методе конечных элементов функцию
где
Рассмотрим следующий простой пример. Пусть в качестве аппроксимирующей функции
Такой конечный элемент называется одномерным симплекс-элементом. Коэффициенты
Графически это можно представить следующим образом (рис.1).
Рисунок 1
Подставив выражение (4) в выражение (3), получим:
Решая систему уравнений (5) относительно
Подставив выражения (6) в выражение (3), получим:
Члены в уравнении (7), заключенные в квадратные скобки, являются функциями формы одномерного симплекс-элемента, т.е.
С учетом введенных обозначений (8) уравнение (7) принимает следующий вид:
В матричной форме выражение (9) запишется в следующем виде
где Аналогично, можно построить функции формы для двумерного симплекс-элемента, который представляет собой плоский треугольник с прямолинейными сторонами (см рис 2). Информационный полином, аппроксимирующий непрерывную функцию
Проделав аналогичные преобразования, можно получить следующие выражения:
Рисунок 2
где
Этап 3. Составление ансамбля конечных элементов, т.е. объединение аппроксимирующих функций элементов в общую модель искомой непрерывной функции. При этом получают систему алгебраических уравнений: j = NФ. (11) Эта система является моделью искомой непрерывной функцией исследуемого объекта. Рассмотрим следующий пример. Пусть рассматриваемый объект состоит из 4-х конечных элементов, т.е. Элемент
Подставив значения номеров узлов из выражений (12) в формулу (9), получим следующую систему алгебраических уравнений вида (11):
В выражениях для функций формы элемента (8) значения произвольных номеров Этап 4. Определение вектора узловых значений искомой непрерывной функции. В общем случае вектор Ф в (11) вначале неизвестен. Его определение — наиболее сложная процедура в методе конечных элементов. Разработано несколько алгоритмов вычисления вектора Ф. Один из алгоритмов основан на минимизации функционала, связанного с физическим смыслом решаемой задачи. Алгоритм состоит из 4 шагов. Шаг 1. Выбор функционала F, зависящего для стационарных задач от искомой функции j и её частных производных F = где V — объём тела. Функционал F представляют в виде суммы соответствующих функционалов, относящихся к отдельным конечным элементам: F = где L — число элементов. Шаг 2. Подстановка аппроксимирующего выражения (10) в (15) и вычисление производных
Шаг 3. Минимизация по вектору Ф функционала F. Для этого составляется уравнение
Суммирование выражений (17) по конечным элементам приводит к системе алгебраических уравнений вида KФ + B = 0, (18) где K — матрица жесткости, Ф — неизвестный вектор узловых значений искомой непрерывной функции; B — вектор нагрузки. Шаг 4. Решение системы (18), позволяющее определить неизвестный вектор узловых значений Ф. Найденные значения вектора Ф подставляют в формулу (11), после чего значения функции j легко вычисляются в любой точке заданной области.
В практических задачах для достижения приемлемой точности решения исследуемый объект разбивается на несколько десятков тысяч элементов с примерно таким же количеством узлов. Поэтому система (18) имеет очень большую размерность. При использовании метода конечных элементов в САПР предварительно вручную проделывают этапы 2 и 4 приведенного алгоритма для конечных элементов установленного типа. В результате для каждого K ( где K ( Полученные для 1. Разбиение исследуемого объекта на конечные элементы заданного типа. 2. Построение разрешающей системы уравнений (18) путём объединения моделей отдельных конечных элементов. 3. Решение полученной системы уравнений, т.е. вычисление вектора узловых значений искомой непрерывной функции. Найденный вектор узловых значений является приближенным решением исходной краевой задачи. 6.2.2. Построение моделей на макроуровне В описании проектируемых объектов на макроуровне характерной особенностью является рассмотрение физических процессов, протекающих в непрерывном времени, но дискретизированном пространстве. На этом уровне в качестве элементов при проектировании объектов машиностроения фигурируют сборочные единицы — детали и узлы. В радиоэлектронике на макроуровне рассматриваются радиоэлектронные схемы, состоящие из таких элементов, как транзисторы, резисторы, конденсаторы, индуктивности, источники тока и напряжения. Типичными математическими моделями на этом уровне являются системы обыкновенных дифференциальных уравнений и уравнений с частными производными и системы алгебраических уравнений в тех случаях, когда анализируются статические состояния объекта или его частотные характеристики. При этом на макроуровне математическая модель объекта проектирования служит для отображения только тех его свойств, которые характеризуют взаимодействие элементов в составе исследуемой системы.
Сама математическая модель проектируемого объекта состоит из совокупности трех типов уравнений: 1) компонентных, 2) топологических и 3) уравнений, необходимых для получения численного решения полученной системы уравнений. Каждое компонентное уравнение описывает процессы определенной физической природы, проходящие в том или ином отдельно рассматриваемом однородное элементе моделируемого объекта. К таким процессам можно отнести механические процессы, электрические, тепловые, гидравлические и т.п. При построении таких компонентных уравнений часто прибегают к методу аналогии, когда строят соответствующие эквивалентные схемы. Такие схемы позволяют выявить те свойства реального объекта, которые, по мнению проектировщика, оказывают самое существенное влияние на функционирование проектируемого объекта или системы. В физически однородных элементах различают элементы емкостного, индуктивного и резисторного типов. Соответствующие им математические модели имеют следующий вид: Таблица соответствий 1
Наряду с компонентными уравнениями в математическую модель системы обязательно входят уравнения, отражающие способ связи элементов системы между собой. Они называются топологическими уравнениями. Топологические уравнения выражают законы сохранения, условия неразрывности, равновесия и т.п. Особенностью топологических уравнений является то, что каждое из них связывает однотипные фазовые переменные, относящиеся к разным элементам моделируемой системы. Отметим, что для компонентных уравнений, о которых говорилось ранее, характерно, что они связывают разнотипные фазовые переменные, относящиеся к одному и тому же элементу системы. Примером топологических уравнений для электрической системы может быть, например, уравнение первого закона Кирхгофа, устанавливающего равенство нулю суммы токов в узлах схемы, т.е.
В общем случае формирование непрерывной математической модели на макроуровне можно представить следующим образом. В общем случае формирование непрерывной математической модели на макроуровне можно представить следующим образом. 1. Выделяют в проектируемой системе однородные физические подсистемы. 2. В библиотеке математических моделей САПР выбирают эквивалентные схемы подсистем, т.е. компонентные уравнения вида:
где
t –независимая переменная, например, время. 3. На основе библиотеки компонентных уравнений элементов составляют подсистему компонентных уравнений математической модели системы F комп(Z, V, t) = 0. (2.16) Эта модель состоит из математических моделей элементов, указанных в перечне составляемой математической модели системы. Рассмотрим следующий пример. Пусть после анализа некоторого проектируемого объекта была получена его эквивалентная схема, вид которой представлен на рис. 2.10. Известна математическая модель полупроводникового диода следующего вида:
где Математические модели остальных четырех элементов следующие:
Рис. 2.10. Эквивалентная схема проектируемого объекта Таким образом, для данного примера имеем 10 неизвестных переменных (токи и напряжения), которые образуют вектор фазовых переменных
и вектор Пять элементов, образующих систему, перечислим в следующем порядке (это важно): Для этих пяти элементов имеем следующую систему компонентных уравнений:
Возвратимся к общей постановке задачи. Для решения полученной системы дифференциальных уравнений После дискретизации системы уравнений
где Выполним разложение системы уравнений (2.17) в ряд Тейлора в окрестностях точки Сохранив в разложении только линейные члены, получим выражения следующего вида:
В выражении (2.18) матрицы Для рассматриваемого примера, воспользовавшись формулами
и вектор правых частей В этих выражениях переменные Таким образом, выражение (2.18) для данного примера примет следующий вид:
4. Определяют межэлементные связи между подсистемами и составляют подсистему топологических уравнений вида
где Подсистема линейных алгебраических уравнений (2.19) выражает законы равновесия и неразрывности для механических систем и законы Кирхгофа – для электрических систем. Существенно, что в эту систему производные, составляющие вектор Для рассмотренного примера выбор системы топологических уравнений вида (2.19) основан на применении законов сохранения токов и напряжений Кирхгофа для выбранной совокупности независимых контуров и сечений в графе эквивалентной схемы. Этот граф для рассматриваемого примера изображен на рис.2.11
Рис. 2.11. Пример графа для данного примера Выбор указанной совокупности независимых контуров и сечений с аналитической точки зрения равнозначен выбору фундаментального дерева в построенном графе. Фундаментальное дерево (остов) - связный суграф, не имеющий циклов, т.е. фундаментальное дерево охватывает все вершины искомого графа и не образует ни одного цикла. Заметим, что суграф - часть графа, образованная удалением из него некоторых ребер, причем число вершин у графа и суграфа одинаково. Выберем фундаментальное дерево графа, состоящее из ветвей d и с,, т.е. это дерево имеет вид, изображенный на рис. 2.12.
Рис. 2.12. Фундаментальное дерево графа Удаленные дуги графа В соответствии с интерпретацией законов Кирхгофа топологическую матрицу d можно представить в следующем виде:
где Матрица Процедура построения Для рассматриваемого примера с учетом последовательности, в которой рассматриваются фазовые переменные, эта
ветвь Следовательно, матрица
Система уравнений вида (2.19), таким образом, будет иметь следующий вид:
5. Совместная система компонентных (2.18) и топологических (2.19) уравнений оказывается не доопределенной, так как включает в себя a уравнений с a + g неизвестными, где a — количество фазовых переменных в векторе V, g – размерность вектора Z. Для доопределения необходимо ввести подсистему уравнений, выражающую формулу численного решения вида
Для большинства методов численного интегрирования подсистема уравнений (2.20) линейна и имеет вид: GkZk,i+ 1 + HkVk,i+ 1 = Lk. (2.21) Таким образом, общая система уравнений математической модели объекта проектирования принимает следующий матричный вид:
Обобщая сказанное, можно сделать вывод, что задача формирования математической модели системы конкретизируется как задача формирования матриц Gk, Hk, D, Aki, Bki и векторов Lk и Qki. Структура матриц Gk, Hk и вектора Lk определяется выбранным методом численного интегрирования системы обыкновенных дифференциальных уравнений. Обратимся опять к нашему примеру. Нетрудно подсчитать, что если воспользоваться только системой уравнений, состоящей из компонентных и топологических уравнений, то эта система не будет доопределенной, так как имеет 12 неизвестных (10 фазовых переменных и 2 переменных типа производных) и 10 уравнений (5 топологических и 5 компонентных). Доопределим эту систему еще двумя уравнениями, воспользовавшись предыдущими рассуждениями для получения выражений для матриц Gk, Hk и вектора Lk.. Так как Для простоты дальнейших преобразований положим, что порядок метода интегрирования равен единице, т.е. Матрица
Таким образом, имеем следующие компоненты системы уравнений вида (2.22):
0 =
После соответствующих преобразований, связанных с умножением матриц, получим следующую систему линейных уравнений:
Эта система уравнений является макромоделью исследуемого (проектируемого) объекта проектирования. Рассмотренный метод формирования математической модели системы называется обобщенным. Его можно применять к моделированию любых технических объектов, если выполняются следующие условия: 1) структуру объекта можно представить в виде совокупности множества элементов и связей между элементами; 2)состояние каждого элемента характеризуется конечным множеством вещественных фазовых переменных, имеющих природу потока (тока) или потенциала (напряжения); 3) для каждого элемента известна математическая модель, связывающая его фазовые переменные между собой. Эти условия выполняются для большинства систем механической, электрической, гидравлической, пневматической, тепловой природы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.131.178 (0.115 с.) |
 ,
, — источник теплоты внутри тела.
— источник теплоты внутри тела.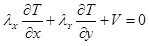 .
.
 –го элемента аппроксимирующей функции
–го элемента аппроксимирующей функции 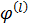 в виде полинома
в виде полинома , (1)
, (1) — вектор–строка коэффициента полинома;
— вектор–строка коэффициента полинома; — свободный член;
— свободный член;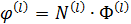 (2)
(2)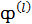 — вектор–столбец узловых значений функции
— вектор–столбец узловых значений функции  — матрица–строка, элементы которой называют функциями формы
— матрица–строка, элементы которой называют функциями формы  (3)
(3)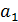 и
и  определяют через узловые значения функции
определяют через узловые значения функции  и
и  в соответствии с условием непрерывности, т.е.
в соответствии с условием непрерывности, т.е. (4)
(4)
 (5)
(5) :
: . (6)
. (6) (7)
(7)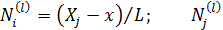 =
=  (8)
(8) . (9)
. (9) (10)
(10) – матрица-строка, элементами которой являются функции форму, а
– матрица-строка, элементами которой являются функции форму, а  – вектор-столбец узловых значений аппроксимируемой функции. Выражение (10) совпадает с выражением (2).
– вектор-столбец узловых значений аппроксимируемой функции. Выражение (10) совпадает с выражением (2). .
.
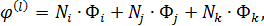

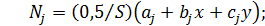
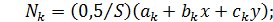
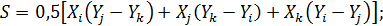

 =
=  ;
; 
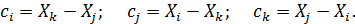
 причем каждый элемент описывается аппроксимирующей функцией вида (9). Можно написать следующее соответствие между произвольными номерами
причем каждый элемент описывается аппроксимирующей функцией вида (9). Можно написать следующее соответствие между произвольными номерами 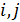 и
и 
 (12)
(12)



 (13)
(13)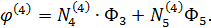

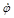 x,
x,  f (j,
f (j,  F (
F ( ) =
) =  f (j (
f (j ( . (16)
. (16) . (17)
. (17) где С, L, R – параметры элементов, физический смысл которых можно пояснить следующей таблицей (см. таблица 1).
где С, L, R – параметры элементов, физический смысл которых можно пояснить следующей таблицей (см. таблица 1). , где
, где  - ток в -й ветви,
- ток в -й ветви,  - множество номеров ветвей, инцидентных рассматриваемому узлу. Другой пример – уравнение Кирхгофа, согласно которому сумма падений напряжений на элементах схемы при их обходе по произвольному контуру равны нулю, т.е.
- множество номеров ветвей, инцидентных рассматриваемому узлу. Другой пример – уравнение Кирхгофа, согласно которому сумма падений напряжений на элементах схемы при их обходе по произвольному контуру равны нулю, т.е.  , где
, где  - номер ветви,
- номер ветви,  - падение напряжения на ветви, входящей в контур с номером
- падение напряжения на ветви, входящей в контур с номером  - множество номеров ветвей, входящих в рассматриваемый контур. Аналогично этим уравнениям для механических поступательных систем справедливо уравнение
- множество номеров ветвей, входящих в рассматриваемый контур. Аналогично этим уравнениям для механических поступательных систем справедливо уравнение  , где
, где  - сила, приложенная к телу (принцип Даламбера) и
- сила, приложенная к телу (принцип Даламбера) и  (сумма абсолютной, относительной и переносной скоростей равна нулю).
(сумма абсолютной, относительной и переносной скоростей равна нулю).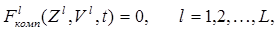 (2.15)
(2.15) — вектор фазовых переменных элемента
— вектор фазовых переменных элемента  ,
, E
E 
 - соответственно напряжение и ток диода,
- соответственно напряжение и ток диода,  - параметры диода.
- параметры диода.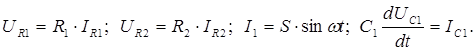


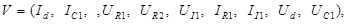

 , состоящий из двух неизвестных переменных – производных соответствующих переменных. Таким образом, имеем 10+2=12 переменных.
, состоящий из двух неизвестных переменных – производных соответствующих переменных. Таким образом, имеем 10+2=12 переменных.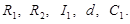

 (см. так же пример) применяют численные методы. Для этого вначале осуществляют дискретизацию системы по времени t, а затем осуществляют разложение полученных уравнений на к - м шаге дискретизации в ряд Тейлора для получения системы линейных уравнений.
(см. так же пример) применяют численные методы. Для этого вначале осуществляют дискретизацию системы по времени t, а затем осуществляют разложение полученных уравнений на к - м шаге дискретизации в ряд Тейлора для получения системы линейных уравнений. , (2.17)
, (2.17)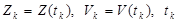 - значение независимой переменной
- значение независимой переменной  на к - м шаге дискретизации.
на к - м шаге дискретизации. , которая является
, которая является  -м приближением к корню этой системы.
-м приближением к корню этой системы. (2.18)
(2.18) и вектор правых частей
и вектор правых частей  определены в точке
определены в точке  , а
, а  есть точка следующего
есть точка следующего  го приближения к корню этой системы.
го приближения к корню этой системы. и
и 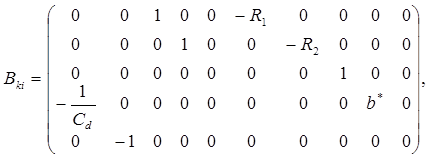
 , где
, где  -
- 

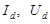 относятся к предыдущей итерации, а
относятся к предыдущей итерации, а 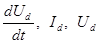 в векторе искомых переменных к данной итерации.
в векторе искомых переменных к данной итерации.



 (2.19)
(2.19) — топологическая матрица инцинденции, показывающая связь между элементами системы. Её элементы есть числа 0, –1, +1.
— топологическая матрица инцинденции, показывающая связь между элементами системы. Её элементы есть числа 0, –1, +1.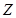 , не входят (более точно – входят с нулевыми коэффициентами). Поэтому более точно систему (2.19) следовало бы записать в виде О
, не входят (более точно – входят с нулевыми коэффициентами). Поэтому более точно систему (2.19) следовало бы записать в виде О  где О – нулевая матрица.
где О – нулевая матрица.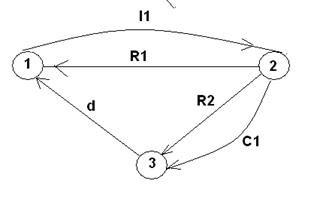
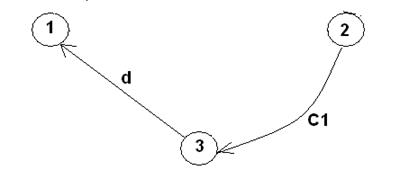
 называют хордами.
называют хордами.
 - единичная матрица,
- единичная матрица,  - топологическая матрица контуров и сечений,
- топологическая матрица контуров и сечений,  - транспонированная матрица
- транспонированная матрица 
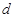 ветвь
ветвь 





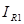
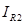


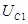



 .
. (2.20)
(2.20) (2.22)
(2.22) - единичная матрица размерности
- единичная матрица размерности  , то делаем вывод, что
, то делаем вывод, что 
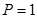 . Тогда
. Тогда  .
. при этом будет иметь следующий вид:
при этом будет иметь следующий вид:

 ;
; 
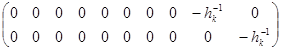 ;
; 
 ;
; ;
; 
 ;
; 
 ;
;  .
. =
=  ;
; 





