
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійна залежність і незалежність векторів. Базис.
Застосовуючи лінійні операції над векторами, можна знаходити вирази вигляду
Які називають лінійними комбінаціями векторів
Вектори
і лінійно незалежними, якщо ця рівність виконується лише за умови, коли всі числа Сукупність лінійно незалежних векторів
Цю рівність називають розкладом вектора Базисом на прямій називають довільний ненульовий вектор на цій прямій. Якщо вектор Базисом на площині називають довільну упорядковану пару неколінеарних векторів. Базисом у просторі називають довільну упорядковану трійку некомпланарних векторів. Якщо вектори
Коефіцієнти Якщо вектори Таким чином, базис у просторі дає змогу кожний вектор одночасно зіставити з упорядкованою трійкою чисел (координатами цього вектора) і, навпаки, кожну упорядковану трійку чисел
Тема 2. Координати вектора. Дії над векторами.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Точку О й упорядковану трійку некомпланарних векторів Точка О – початок координат, а осі, які проходять через початок координат у напрямі базисних векторів, називають осями координат. Упорядковану трійку одиничних попарно ортогональних векторів Прямокутною декартовою системою координат (ПДСК) у просторі називають декартову систему, базис якої ортонормований, і позначають її через
М3
М
Рис.1
Розклад вектора за ортами координатних осей.
Нехай Проведемо через точку М площини, паралельні координатним площинам. Точки перетину цих площин з осями координат позначимо через М1, М2 та М3. Дістанемо прямокутний паралелепіпед, однією з діагоналей якого є вектор Позначимо Враховуючи векторні рівності
дістанемо
Ця формула є основною у векторній алгебрі і називається розкладом вектора Векторну рівність (1) у символічній формі ще записують так:
Довжина вектора. Напрямні косинуси.
Довжину (модуль) вектора
Ця формула безпосередньо випливає з того факту, що квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів його ребер. Оскільки координати вектора де
Рис.2
Тоді Косинуси
Звідси випливає, що орт вектора
де напрямні косинуси визначають за формулою (2).
Дії над векторами.
Нехай вектори задані своїми координатами, тобто
тоді
Іншими словами, при додаванні векторів їхні відповідні координати додають; при множенні вектора на скаляр координати вектора множать на цей скаляр. Вектори
Колінеарність векторів.
З’ясуємо умови колінеарності векторів
Звідси
тобто
Отже, координати колінеарних векторів пропорційні. І навпаки, якщо координати двох векторів пропорційні, то ці вектори колінеарні.
Координати точки.
Довільній точці М простору можна зіставити у ПДСК вектор
Координати х, у, z радіус-вектора Якщо відомі координати початку
Довжину вектора
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.181 (0.028 с.) |
 ,
, ,
, 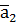 ,…,
,…, 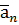 ; числа
; числа  ,
,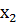 ,…,
,…, 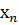 - коефіцієнти.
- коефіцієнти. ,
, 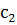 ,…,
,…,  не всі рівні нулю, що лінійна комбінація
не всі рівні нулю, що лінійна комбінація ,
,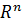 , якщо для кожного вектора з
, якщо для кожного вектора з 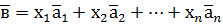 .
. у базисі
у базисі 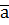 - базис, то існує єдиний розклад вектора
- базис, то існує єдиний розклад вектора  , де
, де  - координата вектора
- координата вектора  - довільний ненульовий вектор площини, то існують сталі
- довільний ненульовий вектор площини, то існують сталі  та
та 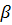 такі, що
такі, що  (рис.12)
(рис.12)
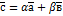
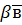
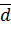 розкладений за базисом, тобто
розкладений за базисом, тобто  , то числа
, то числа 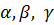 називають координатами вектора
називають координатами вектора  ,
, 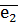 ,
, 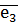 (базису) називають декартовою системою координат у просторі.
(базису) називають декартовою системою координат у просторі.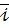 ,
,  ,
, 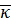 (
( ,
,  ,
,  ) називають ортонормованим базисом.
) називають ортонормованим базисом.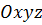 (
( - вісь абсцис,
- вісь абсцис,  - вісь ординат,
- вісь ординат,  - вісь аплікат (рис.1)).
- вісь аплікат (рис.1)).

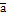 М2
М2 О
О 

 М1 М0
М1 М0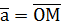 (рис.1).
(рис.1). . Тоді
. Тоді 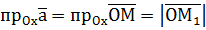 ,
, 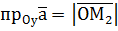 ,
,  .
.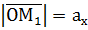 ,
, 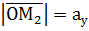 ,
, 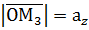 .
. ,
, 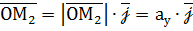 ,
, 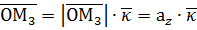 ,
, ,
,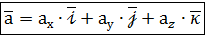 (1)
(1) за ортонормованим базисом
за ортонормованим базисом 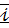 ,
,  ,
,  .
.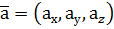 , або
, або  .
.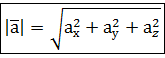

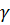 - кути, які вектор
- кути, які вектор 

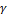


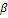
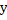

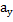
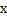
 (2)
(2)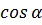 ,
, 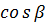 ,
,  кутів
кутів 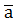 в системі
в системі 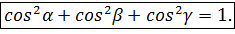
 ,
, ,
,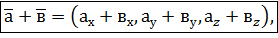

 .
. , тоді
, тоді  - деяке число. Тоді
- деяке число. Тоді .
. ,
, 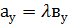 ,
, 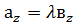
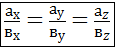 (3)
(3) , який називають радіус-вектором точки М. Тоді існує єдина трійка чисел (х, у, z) така, що
, який називають радіус-вектором точки М. Тоді існує єдина трійка чисел (х, у, z) така, що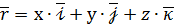 .
.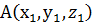 та кінця
та кінця  вектора
вектора  , то його координати знаходять за формулою
, то його координати знаходять за формулою
 (або відстань між точками А та В) записують так:
(або відстань між точками А та В) записують так:



