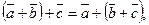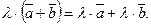Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні операції над векторами.Стр 1 из 4Следующая ⇒
ЗМІСТОВИЙ МОДУЛЬ 2 ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ Тема 2.1. Вектори. 2.1.1. Основні поняття. 2.1.2. Лінійні операції над векторами. 2.1.3. Проекція вектора на вісь. 2.1.4. Розкладання вектора по ортам координатних осей. Модуль вектора. Направляючі косинуси. 2.1.5. Дії над векторами, заданими проекціями.
Тема 2.2. Скалярний добуток вектора і його властивості. 2.2.1. Означення скалярного добутку. 2.2.2. Властивості скалярного добутку. 2.2.3. Вираження скалярного добутку через координати. 2.2.4. Деякі застосування скалярного добутку.
Тема 2.3. Векторний добуток вектора і його властивості. 2.3.1. Означення векторного добутку.
Тема 2.4. Мішаний добуток і його властивості. 2.4.1. Визначення мішаного добутку, його геометричний зміст. 2.4.2. Властивості мішаного добутку. 2.4.3. Вираження мішаного добутку через координати. 2.4.4. Деякі застосування мішаного добутку. Тема 2.1. Вектори. Основні поняття. Величини, що повністю визначаються своїм чисельним значенням, називаються скалярними. Прикладами скалярних величин є: площа, довжина, об'єм, температура, робота, маса. Інші величини, наприклад сила, швидкість, прискорення, визначаються не тільки своїм числовим значенням, але і напрямком. Такі величини називають векторними. Векторна величина геометрично зображується за допомогою вектора. Ø Вектор — це направлений прямолінійний відрізок, тобто відрізок, що має визначену довжину і визначений напрямок. Якщо А — початок вектора, а В – його кінець, то вектор позначається символом Довжиною або модулем вектора Вектор, довжина якого дорівнює одиниці, називається одиничним вектором і позначається через Ø Вектори Колінеарні вектори можуть бути спрямовані однаковоабо протилежно.
Нульовий вектор вважається колінеарним будь-якому векторові. Ø Два вектори З означення рівності векторів випливає, що вектор можна переносити паралельно самому собі, а початок вектора поміщати в будь-яку точку О простору.
рис. 1. На рис. 1 вектори утворюють прямокутник. Справедлива рівність Ø Три вектори в просторі називаються компланарними, якщо вони лежать в одній площині або на паралельних площинах. Якщо серед трьох векторів хоча б один нульовий або два будь-які колінеарні, то такі вектори компланарні. Проекція вектора на вісь. Нехай у просторі задана вісь Ø Проекцією точки Якщо точка
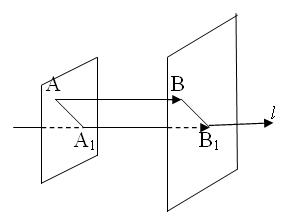
Проекцією вектора протилежно напрямлені (див. рис. 7). Якщо точки Проекція вектора Кут
рис. 8. Розглянемо деякі основні властивості проекцій. Властивість 1. Проекція вектора
рис. 9. □ Якщо Якщо
Якщо Наслідок 1. Проекція вектора на вісь додатна (від’ємна), якщо вектор утворить з віссю гострий (тупий) кут, і дорівнює нулю, якщо цей кут – прямий. Наслідок 2. Проекції рівних векторів на ту саму вісь рівні між собою. Властивість 2. Проекція суми декількох векторів на ту саму вісь дорівнює сумі їхніх проекцій на цю вісь.
□ Нехай, наприклад,
рис. 10. Властивість 3. При множенні вектора □ Таким чином, лінійні операції над векторами приводять до відповідних лінійних операцій над проекціями цих векторів.
Рівність векторів З означення вектора як напрямленого відрізка, який можна пересувати в просторі паралельно самому собі, випливає, що два вектори
Колінеарність векторів З'ясуємо умови колінеарності векторів
Звідси
тобто Таким чином, проекції колінеарних векторів пропорційні. Вірно і зворотне твердження: вектори, що мають пропорційні координати, колінеарні. Координати точки Ø Нехай у просторі задана прямокутна декартова система координат Ø Вектор
Координати точки
рис. 12. Координати вектора Знайдемо координати вектора
Отже, координати вектора дорівнюють різниці відповідних координат його кінця і початку: Тема 2.2. Скалярний добуток вектора і його властивості. Кут між векторами Знаходження кута
Звідси випливає умова перпендикулярності ненульових векторів
Робота постійної сили Нехай матеріальна точка переміщається прямолінійно з положення З фізики відомо, що робота сили
рис. 14. Таким чином, робота постійної сили при прямолінійному переміщенні її точки прикладання дорівнює скалярному добуткові вектора сили на вектор переміщення. Приклад 2.3. Обчислити роботу, зроблену силою ○ Знаходимо
Кут
Тема 2.3. Векторний добуток вектора і його властивості. ЗМІСТОВИЙ МОДУЛЬ 2 ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ Тема 2.1. Вектори. 2.1.1. Основні поняття. 2.1.2. Лінійні операції над векторами. 2.1.3. Проекція вектора на вісь. 2.1.4. Розкладання вектора по ортам координатних осей. Модуль вектора. Направляючі косинуси. 2.1.5. Дії над векторами, заданими проекціями.
Тема 2.2. Скалярний добуток вектора і його властивості. 2.2.1. Означення скалярного добутку. 2.2.2. Властивості скалярного добутку. 2.2.3. Вираження скалярного добутку через координати. 2.2.4. Деякі застосування скалярного добутку.
Тема 2.3. Векторний добуток вектора і його властивості. 2.3.1. Означення векторного добутку.
Тема 2.4. Мішаний добуток і його властивості. 2.4.1. Визначення мішаного добутку, його геометричний зміст. 2.4.2. Властивості мішаного добутку. 2.4.3. Вираження мішаного добутку через координати.
2.4.4. Деякі застосування мішаного добутку. Тема 2.1. Вектори. Основні поняття. Величини, що повністю визначаються своїм чисельним значенням, називаються скалярними. Прикладами скалярних величин є: площа, довжина, об'єм, температура, робота, маса. Інші величини, наприклад сила, швидкість, прискорення, визначаються не тільки своїм числовим значенням, але і напрямком. Такі величини називають векторними. Векторна величина геометрично зображується за допомогою вектора. Ø Вектор — це направлений прямолінійний відрізок, тобто відрізок, що має визначену довжину і визначений напрямок. Якщо А — початок вектора, а В – його кінець, то вектор позначається символом Довжиною або модулем вектора Вектор, довжина якого дорівнює одиниці, називається одиничним вектором і позначається через Ø Вектори Колінеарні вектори можуть бути спрямовані однаковоабо протилежно. Нульовий вектор вважається колінеарним будь-якому векторові. Ø Два вектори З означення рівності векторів випливає, що вектор можна переносити паралельно самому собі, а початок вектора поміщати в будь-яку точку О простору.
рис. 1. На рис. 1 вектори утворюють прямокутник. Справедлива рівність Ø Три вектори в просторі називаються компланарними, якщо вони лежать в одній площині або на паралельних площинах. Якщо серед трьох векторів хоча б один нульовий або два будь-які колінеарні, то такі вектори компланарні. Лінійні операції над векторами. Ø Під лінійними операціями над векторами розуміють операції додавання і віднімання векторів, а також множення вектора на число. Нехай
Ø Вектор
рис. 2. Це правило додавання векторів називають правилом трикутника.Суму двох векторів можна побудуватитакож за правилом паралелограма (див. рис. 3).
рис. 3.
На рис. 4 показане додавання трьох векторів

рис. 4. Ø Під різницеювекторів

рис. 5. Відзначимо, що в паралелограмі, побудованому на векторах
рис. 6. Можна віднімати вектори за правилом: Ø Добутком вектора З означення добутку векторана число випливають властивості цього добутку: 1) якщо 2) завжди Лінійні операції над векторами мають наступні властивості:
Ці властивості дозволяють проводити перетворення в лінійних операціях з вектором так, як це робиться в звичайній алгебрі: доданки змінювати місцями, вводить дужки, групувати, виносити за дужки як скалярні, так і векторні загальні множники. Проекція вектора на вісь. Нехай у просторі задана вісь Ø Проекцією точки Якщо точка

Проекцією вектора протилежно напрямлені (див. рис. 7). Якщо точки Проекція вектора Кут
рис. 8. Розглянемо деякі основні властивості проекцій. Властивість 1. Проекція вектора
рис. 9. □ Якщо Якщо
Якщо Наслідок 1. Проекція вектора на вісь додатна (від’ємна), якщо вектор утворить з віссю гострий (тупий) кут, і дорівнює нулю, якщо цей кут – прямий. Наслідок 2. Проекції рівних векторів на ту саму вісь рівні між собою. Властивість 2. Проекція суми декількох векторів на ту саму вісь дорівнює сумі їхніх проекцій на цю вісь.
□ Нехай, наприклад,
рис. 10. Властивість 3. При множенні вектора □ Таким чином, лінійні операції над векторами приводять до відповідних лінійних операцій над проекціями цих векторів.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.239.148 (0.119 с.) |
 або
або  Вектор
Вектор  (у нього початок у точці B, а кінець у точці A) називається протилежним векторові
(у нього початок у точці B, а кінець у точці A) називається протилежним векторові  , позначається
, позначається  .
.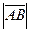 . Вектор, довжина якого дорівнює нулю, називається нульовим векторомі позначається
. Вектор, довжина якого дорівнює нулю, називається нульовим векторомі позначається  . Нульовий вектор напрямку не має.
. Нульовий вектор напрямку не має.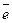 . Одиничний вектор, напрямок якого збігається з напрямком вектора
. Одиничний вектор, напрямок якого збігається з напрямком вектора  .
. називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих; записують
називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих; записують  , якщо вони колінеарні, мають однакові напрямки і однакові дожини.
, якщо вони колінеарні, мають однакові напрямки і однакові дожини.

 але
але  Вектори
Вектори 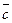 — протилежні,
— протилежні, 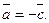 Рівні вектори називають також вільними.
Рівні вектори називають також вільними. , тобто направлена пряма.
, тобто направлена пряма.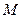 на вісь
на вісь  перпендикуляра
перпендикуляра  , опущеного — з точки
, опущеного — з точки  ). Позначимо через
). Позначимо через  і
і  проекції на вісь
проекції на вісь  .
. якщо вектор
якщо вектор  і вісь
і вісь  збігаються
збігаються  , то проекція вектора
, то проекція вектора  . Якщо
. Якщо  або
або  , то
, то 
 між вектором
між вектором 

 .
.
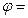

 .
.
 (див. рис. 9).
(див. рис. 9). .■
.■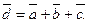 Маємо
Маємо  тобто
тобто  (див. рис. 10.)■
(див. рис. 10.)■
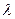 , його проекція на вісь також збільшується на це число, тобто
, його проекція на вісь також збільшується на це число, тобто  .
. При
При  маємо
маємо 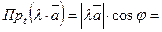 (Властивість 1.)
(Властивість 1.)  . При
. При 
 .■
.■ тобто
тобто
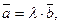 де
де 


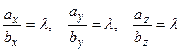 або
або 
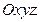 Для будь-якої точки
Для будь-якої точки  називаються координатами точки
називаються координатами точки  тобто
тобто 
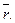 Отже, координати точки – це координати її радіуса-вектора
Отже, координати точки – це координати її радіуса-вектора або
або 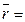
 .
.

 якщо відомі координати точок
якщо відомі координати точок 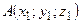 і
і  . Маємо (див. рис. 12.):
. Маємо (див. рис. 12.):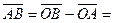




 і
і 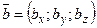 :
: тобто
тобто 


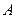 в положення
в положення  під дією постійної сили
під дією постійної сили 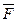 , що утворює кут
, що утворює кут  (див. рис. 14).
(див. рис. 14). дорівнює
дорівнює

 якщо точка її прикладання переміщається прямолінійно з положення
якщо точка її прикладання переміщається прямолінійно з положення  в положення
в положення 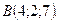 Під яким кутом до
Під яким кутом до  спрямована сила
спрямована сила  Стало бути,
Стало бути,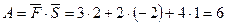 (од. роботи).
(од. роботи). тобто
тобто
 ●
● Від точки А відкладемо вектор
Від точки А відкладемо вектор 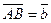 .
. , що з’єднує початок першого вектора з кінцем іншого, називається сумоювекторів
, що з’єднує початок першого вектора з кінцем іншого, називається сумоювекторів 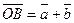 (див. рис. 2).
(див. рис. 2).




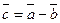 такий, що
такий, що  (див. рис. 5).
(див. рис. 5).
 , тобто віднімання векторів замінити додаванням вектора
, тобто віднімання векторів замінити додаванням вектора  (або
(або  , що має довжину
, що має довжину  , колінеарний векторові
, колінеарний векторові  . Наприклад, якщо дано вектор
. Наприклад, якщо дано вектор  , то вектори
, то вектори 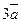 і
і  будуть мати вигляд
будуть мати вигляд  і
і  .
. , то при деякому
, то при деякому 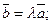
 тобто кожен вектор дорівнює добутковійого модуля на орт.
тобто кожен вектор дорівнює добутковійого модуля на орт.