
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 11 Приклади розв’язання типових задач ⇐ ПредыдущаяСтр 5 из 5
Приклад 1 На основі даних, наведених у табл. встановити наявність кореляційного зв’язку, визначити лінію регресії за лінійною моделлю. Оцінити істотність і щільність зв’язку. Залежність між факторною (х) та результативною (у) ознаками
Розв’язання: Математично лінійний зв’язок у загальному вигляді записується рівнянням:Y = a + bx, де Y – результативна ознака, а – параметр рівняння, який характеризує початковий рівень; b – параметр рівняння, який характеризує середній абсолютний приріст; х – факторна ознака. Параметри рівняння регресії визначаються методом найменших квадратів, основна умова якого – мінімізація суми квадратів відхилень емпіричних значень (y) від теоретичних Y: де у – емпіричні значення результативної ознаки; Y – теоретичні значення результативної ознаки. Математично доведено, що значення параметрів a та b, при яких мінімізується сума квадратів відхилень, визначаються із системи нормальних рівнянь:
Допоміжна таблиця для розрахунку параметрів лінійної моделі
Використовуючи дані наведеної таблиці, знаходимо параметри лінійного рівняння:
Таким чином, лінія регресії має вигляд: у = 25,57 + 0,408 х. Для оцінки істотності та щільності лінійного зв’язку використовується лінійний коефіцієнт кореляції (Пірсона) r: де Для обчислення коефіцієнта кореляції Пірсона складемо допоміжну таблицю. Допоміжна таблиця для обчислення коефіцієнта кореляції Пірсона
Тоді: Для n= 8, rкр = 0,71. Оскільки розраховане значення коефіцієнта кореляції Пірсона більше за його критичне значення, то зв’язок є істотним. Коефіцієнт кореляції Пірсона набуває значень у межах Відповідь: лінія регресії має вигляд: у = 25,57 + 0,408· х; лінійний коефіцієнт кореляції Пірсона r = 0,997 свідчить про щільний прямий зв’язок. Приклад 2 Дані про споживання м’яса в сім’ях робітників та службовців з різним рівнем середньодушового сукупного доходу наведено у таблиці:
Встановити взаємозв’язок та оцінити його істотність і щільність за допомогою методу аналітичного групування. Розв’язання: Розрахуємо середні величини в кожній групі за формулою середньої арифметичної простої:
Тоді:
Середню з групових дисперсій розрахуємо за формулою: Міжгрупову дисперсію обчислимо за формулою:
Обчислимо кореляційне відношення: Критичне значення кореляційного відношення для обсягу сукупності 20 одиниць та трьох груп дорівнює 0,318. Відповідь: Оскільки розраховане кореляційне відношення більше за його критичне значення, між рівнем середньодушового доходу та споживанням м’яса існує прямий щільний зв’язок.
Тема 12Приклади розв’язання типових зада Приклад 1 Під час безповторного вибіркового спостереження, яке проводилось в одній з крамниць продажу дешевого одягу були отримані такі дані:Розподіл проданого товару за цінами
Визначити середню ціну та граничну помилку з імовірністю 0,954; побудувати довірчий інтервал для середньої ціни. Загальна кількість товарів (обсяг генеральної сукупності) 3254 одиниць. Розв’язання: Для розрахунку середньої ціни за одиницю проданого товару замінимо спочатку інтервальний ряд розподілу дискретним. Використовуючи прийняте у статистиці припущення, що в межах одного інтервалу розподіл уважається рівномірним, значення ознаки (у даному прикладі ціна на товар) замінюємо на відповідні середні значення, які розраховуються за формулою: Маємо такі значення:
З урахуванням обчислених значень середин інтервалів, вихідні дані набувають такого вигляду: Дискретний ряд розподілу проданого товару за цінами
Середня ціна обчислюється за формулою середньої арифметичної зваженої:
тобто межі довірчого інтервалу становитимуть:3,2 – 0,32 ≤ це означає, що середня ціна за одиницю проданого товару може коливатися від 2,88 до 3,52 грн. у генеральній сукупності, яка складається із 3254 одиниць товару, Приклад 2 Під час безповторного вибіркового спостереження в одному з судів з метою дослідження термінів позбавлення волі засуджених за тяжкі злочини були отримані такі дані: Розподіл засуджених за тяжкі злочини за терміном позбавлення волі (дані умовні)
Визначити середній термін позбавлення волі та довірчий інтервал з імовірністю 0,954. Загальна кількість засуджених за тяжкі злочини протягом досліджуваного періоду в цьому суді становила 986 осіб.
Розв’язання: Маємо дискретний ряд розподілу, тому середній термін позбавлення волі за тяжкі злочини на підставі вибіркових даних обчислюється за формулою середньої арифметичної зваженої: де t – довірче число, або квантиль розподілу, який для великої за обсягом вибірки (n > 30) визначається з таблиць нормального розподілу та для ймовірності 0,954 дорівнює 2;
Тепер обчислюється гранична помилка: Довірчий інтервал можна записати таким чином: Відповідь: середній термін позбавлення волі за тяжкі злочини за даними вибіркової сукупності дорівнює 6,9 років; з імовірністю 0,954 можна стверджувати, що середній термін позбавлення волі за тяжкі злочини у генеральній сукупності не менше як 6,7 років та не перевищує 7,1 років (або знаходиться в межах від 6,7 до 7,1 років). Приклад 3 За звітний період у суді було розглянуто 480 кримінальних справ, за якими проходило 650 злочинців. Розподіл засуджених за віком у вибірці наведений у табл. Визначити частку неповнолітніх злочинців та довірчий інтервал частки цих засуджених з імовірністю 0,954. Розподіл засуджених за віком за звітний період (дані умовні)
Розв’язання:Частка неповнолітніх злочинців визначається як питома вага кількості злочинців відповідної вікової групи у загальному обсязі вибіркової сукупності, тобто:р = хі / å хі, де хі – кількість неповнолітніх злочинців у вибірці; å хі – загальна кількість злочинців, які потрапили до вибірки. Тоді:р = 14 / 65 = 0,215. Оскільки обсяги генеральної сукупності та вибірки великі, то для визначення граничної помилки використаємо формулу:∆w = p – частка неповнолітніх злочинців у вибірці; q – частка повнолітніх злочинців у вибірці; n – обсяг вибірки. Оскільки сумарна кількість неповнолітніх та повнолітніх злочинців дорівнює обсягу вибірки, то q = 1 – p, тоді:
q = 1 – 0,215 = 0,785. Тоді довірчий інтервал: Приклад 4 Визначити оптимальний обсяг вибірки для повторного механічного відбору з імовірністю 0,954 за умови, що вік працюючих у генеральній сукупності коливається від 16 до 62 років, а гранична помилка середнього віку працюючих не повинна перевищувати 2 роки.Розв’язання:Оптимальний обсяг вибірки для повторного механічного відбору обчислюється за формулою:
Оскільки гранична помилка не повинна перевищувати 2 роки, то обсяг вибірки округлюємо у більший бік незалежно від того, яка цифра стоїть після цілого числа.Таким чином, можна зробити висновок - з імовірністю 0,954 можна стверджувати, що оптимальний обсяг вибірки має бути 60 одиниць. Приклад 5 Визначити оптимальний обсяг вибірки для безповторного механічного відбору для визначення частки якісної продукції з імовірністю 0,954 за умови, що обсяг генеральної сукупності дорівнює 2740 виробів, а гранична помилка якісної продукції не повинна перевищувати 0,2.Розв’язання:Оптимальний обсяг вибірки для повторного механічного відбору обчислюється за формулою:
Тоді оптимальний обсяг вибірки: Таким чином, можна зробити висновок - з імовірністю 0,954 можна стверджувати, що за таких умов оптимальний обсяг вибірки має бути 25 одиниць.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.238.20 (0.034 с.) |
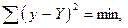
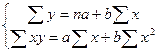 . Розв’язавши цю систему, знаходимо такі значення параметрів:
. Розв’язавши цю систему, знаходимо такі значення параметрів: 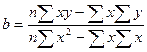 ;
;  . Для визначення параметрів лінійного рівняння складемо допоміжну таблицю.
. Для визначення параметрів лінійного рівняння складемо допоміжну таблицю.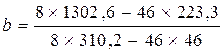 = 0,408
= 0,408 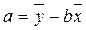 = 223,3 / 8 – 0,408 × 46 / 8 = 25,57.
= 223,3 / 8 – 0,408 × 46 / 8 = 25,57.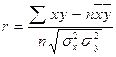 ,
,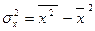 – факторна дисперсія;
– факторна дисперсія;  – загальна дисперсія.
– загальна дисперсія. 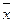 – середнє значення факторної ознаки;
– середнє значення факторної ознаки; 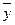 – середнє значення результативної ознаки;n – кількість пар ознак.
– середнє значення результативної ознаки;n – кількість пар ознак.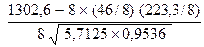 = 0,997.
= 0,997.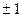 , тому ха-рактеризує не лише щільність, а й напрямок зв’язку. Додатне значення свідчить про прямий зв’язок, а від’ємне – про зворотний.
, тому ха-рактеризує не лише щільність, а й напрямок зв’язку. Додатне значення свідчить про прямий зв’язок, а від’ємне – про зворотний.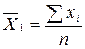 = (48 + 62 + 40 + 52 + 50 + 36) / 6 = 48;
= (48 + 62 + 40 + 52 + 50 + 36) / 6 = 48; 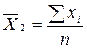 = (91 + 96 + 84 + 95 + 98 + 94 + 92 + 89 + 98 + 92) / 10 = 84,6;
= (91 + 96 + 84 + 95 + 98 + 94 + 92 + 89 + 98 + 92) / 10 = 84,6;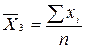 = (100 + 112 + 108 + 110) / 4 = 107,5. Загальну середню для всієї сукупності обчислимо за формулою середньої арифметичної зваженої, де в якості окремих ознак беруться середні кожної групи, а частотами є обсяги відповідних груп:
= (100 + 112 + 108 + 110) / 4 = 107,5. Загальну середню для всієї сукупності обчислимо за формулою середньої арифметичної зваженої, де в якості окремих ознак беруться середні кожної групи, а частотами є обсяги відповідних груп: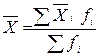 = (48 × 6 + 84,6 × 10 + 107,5 × 4) / 20 = 78,2. Визначаємо групові дисперсії за формулою:
= (48 × 6 + 84,6 × 10 + 107,5 × 4) / 20 = 78,2. Визначаємо групові дисперсії за формулою: 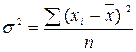 .
.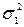 = [(48 – 48)2 + (62 – 48)2 + (40 – 48)2 + (52 – 48)2 + (50 – 48)2 ++ (36 – 48)2 ] / 6 ≈ 70,67;
= [(48 – 48)2 + (62 – 48)2 + (40 – 48)2 + (52 – 48)2 + (50 – 48)2 ++ (36 – 48)2 ] / 6 ≈ 70,67;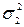 = [(91 – 84,6)2 + (96 – 84,6)2 + (84 – 84,6)2 + (95 – 84,6)2 + (98 – 84,6)2 ++ (94 – 84,6)2 + (92 – 84,6)2 + (89 – 84,6)2 + (98 – 84,6)2 + (92 – 84,6)2 ] / 10 = 85,58;
= [(91 – 84,6)2 + (96 – 84,6)2 + (84 – 84,6)2 + (95 – 84,6)2 + (98 – 84,6)2 ++ (94 – 84,6)2 + (92 – 84,6)2 + (89 – 84,6)2 + (98 – 84,6)2 + (92 – 84,6)2 ] / 10 = 85,58;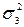 = [(100 – 107,5)2 + (112 – 107,5)2 + (108 – 107,5)2 + (110 – 107,5)2] / 4 = = 20,75.
= [(100 – 107,5)2 + (112 – 107,5)2 + (108 – 107,5)2 + (110 – 107,5)2] / 4 = = 20,75.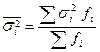 = (70,67 × 6 + 85,58 × 10 + 20,75 × 4) / 20 = 68,14.
= (70,67 × 6 + 85,58 × 10 + 20,75 × 4) / 20 = 68,14.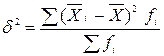
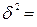 [(48 – 78,2)2 × 6 + (84,6 – 78,2)2 ×10 + (107,5 – 78,2)2 × 4] / 20 = 465,79. Використовуючи правило складання дисперсій
[(48 – 78,2)2 × 6 + (84,6 – 78,2)2 ×10 + (107,5 – 78,2)2 × 4] / 20 = 465,79. Використовуючи правило складання дисперсій 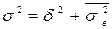 , визначимо загальну дисперсію:
, визначимо загальну дисперсію: 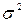 = 465,79 + 68,14 = 533,93.
= 465,79 + 68,14 = 533,93.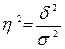 = 465,79 / 533,93 = 0,872.
= 465,79 / 533,93 = 0,872.
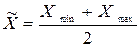 ,де
,де 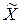 – середина інтервалу;Хmin – нижня межа певного інтервалу;Хmax – верхня межа певного інтервалу.
– середина інтервалу;Хmin – нижня межа певного інтервалу;Хmax – верхня межа певного інтервалу.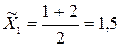 ;
; 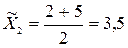 ;
; 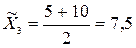 ;
; 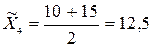 .
.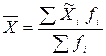 .Тоді середня ціна за даними вибіркового спостереження:
.Тоді середня ціна за даними вибіркового спостереження: 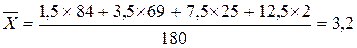 грн.Гранична помилка для безповторного випадкового відбору розраховується за формулою:
грн.Гранична помилка для безповторного випадкового відбору розраховується за формулою: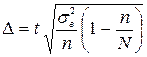 ,де t – довірче число (або квантиль розподілу), яке для великої за обсягом вибірки (більше 30 одиниць) для ймовірності 0,954 дорівнює 2;
,де t – довірче число (або квантиль розподілу), яке для великої за обсягом вибірки (більше 30 одиниць) для ймовірності 0,954 дорівнює 2; 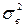 – дисперсія вибірки;n – обсяг вибірки;N – обсяг генеральної сукупності.Дисперсія вибірки обчислюється за формулою:
– дисперсія вибірки;n – обсяг вибірки;N – обсяг генеральної сукупності.Дисперсія вибірки обчислюється за формулою: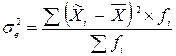 ,де
,де 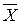 – середня арифметична (середня ціна)fi – частота (кількість проданого товару) кожного окремого інтервалу.Таким чином, дисперсія вибірки:
– середня арифметична (середня ціна)fi – частота (кількість проданого товару) кожного окремого інтервалу.Таким чином, дисперсія вибірки: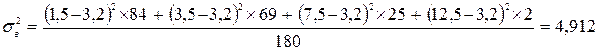 .Тепер можна визначити граничну помилку:
.Тепер можна визначити граничну помилку: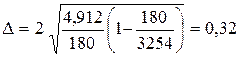 .Таким чином,
.Таким чином, 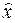 ≤ 3,2 + 0,32,
≤ 3,2 + 0,32,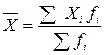 .Тоді
.Тоді 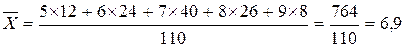 (років)Для визначення довірчого інтервалу спочатку потрібно обчислити граничну помилку за формулою:
(років)Для визначення довірчого інтервалу спочатку потрібно обчислити граничну помилку за формулою: 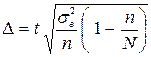 ,
,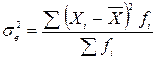
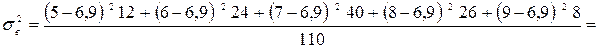 =
= 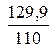 = 1,181.
= 1,181.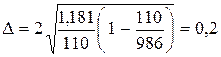 .
.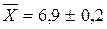 , або
, або 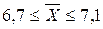 .
.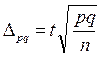 =
= 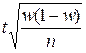 ,де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2;
,де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2;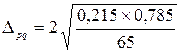 = 0,1.Довірчий інтервал записується у вигляді: р = 0,215
= 0,1.Довірчий інтервал записується у вигляді: р = 0,215 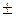 0,1 або 0,115
0,1 або 0,115 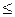 р
р 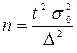 ,де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2;
,де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2; 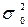 – дисперсія генеральної сукупності;D – гранична помилка.Оскільки дисперсія генеральної сукупності невідома й відсутні дані щодо аналогічних досліджень, то для визначення дисперсії скористаємося правилом трьох сигм, тобто:
– дисперсія генеральної сукупності;D – гранична помилка.Оскільки дисперсія генеральної сукупності невідома й відсутні дані щодо аналогічних досліджень, то для визначення дисперсії скористаємося правилом трьох сигм, тобто: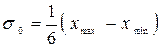 .Тоді:
.Тоді: 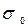 = 1 / 6 (62 – 16) = 7,7.Тоді оптимальний обсяг вибірки становитиме:n = 2 2 × 7,7 2 / 2 2 = 60.
= 1 / 6 (62 – 16) = 7,7.Тоді оптимальний обсяг вибірки становитиме:n = 2 2 × 7,7 2 / 2 2 = 60.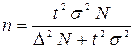 ,де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2N – обсяг генеральної сукупності;
,де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2N – обсяг генеральної сукупності;  – дисперсія генеральної сукупності;D – гранична помилка.Для частки (альтернативної ознаки), коли відсутня будь-яка інформація про структуру сукупності, уважають, що частка р = 0,5, отже:
– дисперсія генеральної сукупності;D – гранична помилка.Для частки (альтернативної ознаки), коли відсутня будь-яка інформація про структуру сукупності, уважають, що частка р = 0,5, отже: 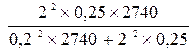 = 25.
= 25.


