
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сосредоточенный источник тепла
Рассмотрим нестандартную задачу о теплопроводности при наличии в точке x = ξ сосредоточенного источника тепла. В этой точке решение задачи
Удовлетворяющий начальному условию
И краевым условиям
удовлетворяет условиям сопряжения
Где Q=Q(t) – мощность источника. Условие разрыва теплового потока Предположим, что сетка
Тогда во всех узлах
Напишем уравнение баланса для интервался Будем иметь
Совершая отсюда обычный переход к разностному уравнению, получаем
Таким образом, схема имеет вид:
Где
и краевыми условиями:
Пользуясь уравнением баланса, преобразуем выражение к виду
Для определенности будем считать, что
По аналогии со случаем разрывных коэффициентов находим
Учитывая затем, что
Находим
Нетрудно заметить также, что
Однако в данном случае выбор коэффициента
Цилиндрически-симметричные задачи теплопроводности
При изучении процессов теплопроводности или диффузии в телах, имеющих форму цилиндра, естественно пользоваться цилиндрической системой координат (r, ϕ, z). Если температура не зависит от ϕ и z, то мы приходим к уравнению
При x=1 будем ставить обычное условие (первого или третьего рода), например,
а при х = 0 естественное условие ограниченности решения
Рассмотрим задачу
Введем равномерную сетку на отрезке
На отрезке
Где
Чтобы получить разностное краевое условие при x = 0, воспользуемся условием
для стационарного уравнения и заменим в нем В результате получаем краевое условие
которое можно также записать в виде
Присоединяя сюда условия при х=1 и t= 0, получаем разностную краевую задачу
Где,
Квазилинейное уравнение теплопроводности
Между тем для высокотемпературных процессов, протекающих, например, в плазме, коэффициент теплопроводности является нелинейной функцией температуры (и плотности), а в ряде задач, кроме того, функцией градиента температуры. Далее, источники тепла (правые части в уравнении теплопроводности) могут зависеть от температуры, если, например, тепло выделяется в результате химической реакции. От температуры может зависеть и теплоемкость среды. Рассмотрим теперь два типа чисто неявных схем (схем с опережением, а=1) для простейшего квазилинейного уравнения теплопроводности
где Схема а):
Схема б):
где
например,
От способа вычисления
Относительно
|
|||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.122.162 (0.01 с.) |

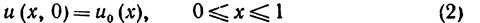


 означает что разрывные первые производные
означает что разрывные первые производные  , т.е. решение u=u(x,t) имеет на прямой x = ξ слабый разрыв. Чтобы написать однородную разностную схему, учитывающую источник Q при x = ξ, воспользуемся интегро-интерполяционным методом.
, т.е. решение u=u(x,t) имеет на прямой x = ξ слабый разрыв. Чтобы написать однородную разностную схему, учитывающую источник Q при x = ξ, воспользуемся интегро-интерполяционным методом. равномерна и
равномерна и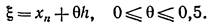
 разностное уравнение имеет обычный вид
разностное уравнение имеет обычный вид

 при фиксированном
при фиксированном 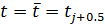 . Учитывая, что
. Учитывая, что 

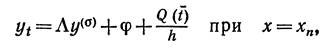


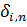 —символ Кронекера. Для погрешности z = y—u получаем уравнение с правой частью
—символ Кронекера. Для погрешности z = y—u получаем уравнение с правой частью


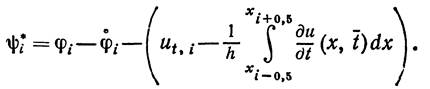
 , т.е.
, т.е.  Тогда
Тогда




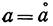 не улучшает порядка точности. Из формулы
не улучшает порядка точности. Из формулы  видно, что
видно, что  и» следовательно,
и» следовательно,  , если
, если  , т.е. источник находится в узле сетки.
, т.е. источник находится в узле сетки.
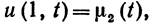

 (1)
(1)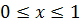 :
:

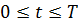 . Оператор L, аппроксимируем разностным оператором
. Оператор L, аппроксимируем разностным оператором
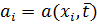 и уравнению (1) поставим в соответствие схему с весами
и уравнению (1) поставим в соответствие схему с весами

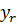 на
на 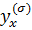 , затем
, затем  , а u на y.
, а u на y.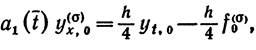








 (1)
(1) (2)
(2) (3)
(3) сильно зависит точность расчета температурной волны. Проведенные численные эксперименты для случая, когда
сильно зависит точность расчета температурной волны. Проведенные численные эксперименты для случая, когда  есть степенная функция температуры, показывают, что формулой (3) для
есть степенная функция температуры, показывают, что формулой (3) для 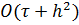 . Обе они абсолютно устойчивы. Схема а) линейна относительно значения функции
. Обе они абсолютно устойчивы. Схема а) линейна относительно значения функции  на слое
на слое  и значения функции
и значения функции  на слое
на слое  например, методом прогонки. Поскольку схема а) абсолютно устойчива, шаг τ выбирается только из соображений точности. Схема б) не линейна относительно функции
например, методом прогонки. Поскольку схема а) абсолютно устойчива, шаг τ выбирается только из соображений точности. Схема б) не линейна относительно функции 
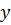 разностная схема оказывается линейной. В качестве начальной итерации берется функция у предыдущего шага по времени:
разностная схема оказывается линейной. В качестве начальной итерации берется функция у предыдущего шага по времени: 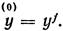 Практически оказывается достаточным сделать две-три итерации. Даже в том случае, если итерации не сходятся, для повышения точности схемы оказывается полезным сделать две итерации.
Практически оказывается достаточным сделать две-три итерации. Даже в том случае, если итерации не сходятся, для повышения точности схемы оказывается полезным сделать две итерации.



