
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события: виды событий, действия над событиями. Свойства действий над событиямиСтр 1 из 4Следующая ⇒
Случайные события: виды событий, действия над событиями. Свойства действий над событиями Под эксп-том или опытом или испытанием в т.в. понимается некая сов-ть действий, осуществляемых при строго фиксируемых и контролируемых усл-ях. Важной хар-кой эксп-та в т.в. явл. возм-ть его неоднокрю реализации, т.е. каждый эксп-т т.в. можно хотя бы в принципе повторить неск. раз. Пространство элем. исходов (Ω)- мн-во, содерж. все возможные рез-ты данного случ. эксп-та, из кот. в эксп-те происходит ровно один. Элем-ты этого мн-ва- элементарные исходы (ωi). События-подмн-ва мн-ва Ω. Говорят, что в рез-те эксп-та произошло соб. А, если А принадл. Ω, т.е. если в эксп-те произошел один из элем. исходов, входящих в А. Виды соб-тий Достоверное соб- соб., кот обязательно произойдет а рез-те эксп-та, т.к. эт единств. соб, включ. все элем. исходы (Ω). Невозм. соб.- соб., кот. заведомо не может произойти, в рез-те эксп-та, т.е. это соб., не сод. ни одного элем. исхода (Ø). Заметим, что Ø принадл.Ω. Случ. соб.-соб, кот. в рез-те эксп-та может либо произойти, либо не произ. Действия над событиями
Свойства действий над соб. Законы де Моргана:
2. Частота и относительная частота события. Свойства относительной частоты. Вероятность случайного события. Связь между вероятностью и относительной частотой.
Частота события Рассмотрим некот. опыт и связ. с ним случ. соб. А. Предположим, что опыт был повторен n раз, обозн. К -кол-во появл. А в опыте (абсолютная частота события). Очев, что К≤n, число Св-ва отн. частоты 1 2. 3. 4. Если A, B- несовм., то 5.Cвойство устойчивости частоты: если провести неск. серий из n испыт., то На основе данного св-ва можно сформировать статистическое определ. вер-ти: Если при большом числе испыт. А 1 2. 3. 4. Если A, B- несовм., то Геометрическая вероятность Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике же существуют опыты, где множество исходов равно бесконечности. Чтобы преодолеть недостаток определения классической вероятности (то, что оно неприменимо к опытам с бесконечным числом исходов), вводят понятие геометрической вероятности, то есть вероятности попадания некоторой точки в область. Пусть в некоторую область случайно бросается точка Т, причем все точки, принадлежащие этой области Р(А)=
Рассмотрим пример. Задача о встрече. Оля и Ира договорились встретиться в промежутке от 2 до 3 часов дня. Та, кто придет первой, ждет 10 минут и уходит. Найти вероятность встречи. Решение: Примем временной промежуток между 14:00 и 15:00 за числовой отрезок от 0 до 1. Пусть х – момент прихода Оли, а у – момент прихода Иры, Ω - все возможные моменты прихода. Причем значения х и у принадлежат промежутку от 0 до 1. Событие А состоит в том, что разница между моментами прихода девочек составит не более 10 минут, потому что именно в этом случае они встретятся.
Таким образом, событие А={(x;y): |x-y| |x-y| Раскрыв знак модуля, получаем два равенства: х-у= 1/6 и х-у= -1/6. Оба эти равенства представляют собой линейные функции, графиком которых служит прямая линия.
Где квадрат со стороной 1 – пространство элементарных исходов, а заштрихованная область –исходы, благоприятствующие событию А. Далее по определению геометрической вероятности можно найти вероятность события А как отношение площадей заштрихованной области и квадрата (заштрихованная область= площадь квадрата – 2 треугольничка). В итоге получаем 11/36. Вероятность суммы событий Раннее было сформулировано, что вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. P(A+B)=P(A)+P(B) (A и B-несовместные) Сумма нескольких событий называют событие, которое состоит в появлении хоть одного из этих событий. Теорема Вероятность суммы нескольких попарно несовместных событий, те появление хотя бы одного из них (неважно какого) равна сумме их вероятностей. A1..An-попарно несовместные, то P(A1+…An)=P(A1)+…+P(An) Доказательство A1,A2,A3-попарно несовместные A1 A2=∅, A1A3=∅, A2A3=∅, то P(A1+A2+A3)= P((A1+A2)+A3) = P(A1+A2) + P(A3) = P(A1)+P(A2)+P(A3) Т. Сложения для совм событий Т: вер-ть появл-я хоть 1 из 2х совм соб-ий равна сумме вер-тей этих соб-ий минус вер-ть их совмест появл-я. A и B-совмест, то P(A+B)=P(A)+P(B)-P(AB) Док-во Тк A и B по усл совм, то событие A+B наступит, если произойдет 1 из след несовм соб-ий: AB, A Тк они несовм, то применим теор о слож-ии для несовм соб-ий P(A+B)= P(A Рассм соб-е A: по св-ву действий над соб-ями P(A)=P(AB)+P(A P(A Рассм соб-е B: P(B)=P(AB)+P( P( Подставим (v) и (w) в (**): P(A+B)=P(A)-P(AB)+P(B)-P(AB)+P(AB) P(A+B)=P(A)+P(B)-P(AB)-для совм Замечание Если A и B несовм, то AB= P(A+B)=P(A)+P(B) для несовм Формула полной вероятности пусть А может наступить лишь при условии одного из попарно несовместных событий Н1, Н2,…,Нn, Образующих полную группу (попарно несовместные означает 1)Hi*Hj= невозможному событию, при любом I ≠ j 2) Н1+Н2+…+Нn= Ω) пусть известны вероятности событий, а так же известны P(A|H1) P(A|H2)… P(A|Hn) ТЕОРЕМА(формула полной вероятности): Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий Н1, Н2,…,Нn, образующ. полную группу, равна сумме произведения вероятностей каждого из этих событий на соответствующие условные вероятности события А, т.е. P(A)= P(H1)*P(A|H1)+ P(H2)*P(A|H2)+…+ P(Hi)*P(A|Hn) ДОК-ВО: т.к. по условию событие А может наступить, если наступить одно из несовместных событий Н1, Н2,…,Нn, то появление события А означает появление одного из несовместных событий А*Н1, А*Н2,…,А*Нn, тогда по теореме сложения для несовместных событий получим: P(A)=P(A*H1)+ P(A*H2)+… P(A*Hn) где вероятность произведения найдем по теореме умножения для зависимых событий: P(A)= P(H1)*P(A|H1)+ P(H2)*P(A|H2)+…+ P(Hi)*P(A|Hn) ч.т.д. (P(H1)+P(H2)+…+P(Hn)=1) Hi-гипотезы, тк заранее неизвестно, которая из них наступит Формула Байеса. пусть А может наступить лишь при условии одного из событий Н1, Н2,…,Нn, Образующих полную группу. Допустим, что в результате испытание А уже наступило, наша задача попытаться переоценить вероятность гипотез после завершения А.
т.е. P(H1|A), P(H2|A), …, P(Hn|A) найдем, например P(H1|A) по теореме умножения для зависимых событий имеем: P(AH1)=P(H1)*P(A|H1) => P(H1)*P(A|H1)=P(A)*P(H1|A) => P(AH1)=P(A)*P(H1|A)
выразим P(H1|A)
Числовые характеристики НСВ 1)Матем.ожидание нсв Х опред-ся равен-вом: M(X)= Если все возм.знач-я Xϵ [a;b], то M(X)= 3) Дисперсия нсв опр-ся рав-вом: D(X) = Если все возм.знач-я Xϵ [a;b], то D(X)= 4)Среднее квадратич. отклонение. Ϭ(X)= 5) Модой нсв X наз-ся то ее знач. аргемента, в кот. плот-ть достиг. max
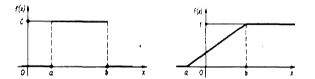
6) Медианой нсв X наз-ся то ее знач. арг-та, для кот. выполн-ся: Me(X)= Равномерное распределение НСВ (непрерывная случайная величина) Х распределена равномерно на [a; b], если ее Функция распределения выражается формулой: F(x)= Графики функций f(x) и F(x) имеют вид:
M(X)=Me(X)= Используя формулу для вычисления математического ожидания НСВ, имеем:
Таким образом, математическое ожидание случайной величины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка. D(X)= Сигма σ(X)= Mo(X) это любая точка из [a;b]: бесконечное множество. Основное свойство закона равном распределения НСВ на отрезке: вероятность попадания СВ в интервал от α до β из области определения функции пропорциональна длине этого интервала:
Равномерное распределение имеют СВ, характеризующие ошибки измерений при помощи инструмента с крупными делениями при округлении. Нормальное распределение СВ Х распределена по нормальному закону, если
Где а и s—некоторые постоянные, называемые параметрами нормального распределения, которых достаточно для задания норм распр. a=M(X) s=s(X) График плотности – нормальная кривая Гаусса. Исследуем ее, чтобы построить: 1°. Областью определения функции f(x) является вся числовая ось. 2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0. 3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции. 4°. Функция f{x) имеет в точке х = a максимум, равный
5°. График функции f(x) симметричен относительно прямой х = а. 6°. Нормальная кривая в точках х = а +s имеет перегиб,
На основании доказанных свойств построим график плотности нормального распределения f(x).
Выясним влияние а и s: 1. Изменение а не изменяет форму кривой, но приводит к ее сдвигу вдоль Ох вправо при возрастании а и влево при убывании 2. При увеличении s нормальная кривая становится более пологой, при уменьшении – более острой 3. При любых а и s площадь под графиком равна 1. Для вычисления вероятности попадания в интервал вводится функция Лапласа
Свойства:
Φ(0)=0 При f(x)˃5 Φ(x)=0,5 Для вычисления вероятности попадания
Часто необходимо вычислить вероятность отклонения нормального распределения Х по абсолютной величине, не большей заданного положительного числа.
(функция Лапласа—нечетная), окончательноимеем
Чем меньше Свойства дисперсии СВ Свойство 1. Дисперсия постоянной величины С равна нулю: D (C)=0 Док-во: По определению D, D (C)=M{[C-M(C)]2}. Пользуясь первым свойством мат ожид (мат ожид постоянной равно самой постоянной), получим D(C)=M[(C-C)2]=M(0)=0. Следовательно, D(C)=0. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)=C2D(X). Док-во: По опр D имеем:D(CX)=M{[CX-M(CX)]2}.Пользуясь вторым свойством мат ожид (пост множитель можно выносить за знак мат ожид), получим: D(CX)=M{[CX-CM(X)]2}=M{C2[X-M(X)]2}=C2M{[X-M(X)]2}=C2D(X). Сл-но, D(CX)=C2D(X). Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y). Док-во: По формуле для вычисления дисперсии имеем: D(X+Y)=M[(X+Y)2]-[M(X+Y)]2. Раскрыв скобки и пользуясь сво-ми мат ожид суммы нескольких величин и произведения двух независимых случайных величин, получим D(X+Y)=M(X2)+2M(X)*M(Y)+M(Y2)-M2(X)-2M(X)*M(Y)-M2(Y)={M(X2)-[M(X)]2}+{M(Y2)-[M(Y)]2}=D(X)+D(Y) Следствие 1. Дисп суммы нескольких взаимно независимых св равна сумме дисперсий этих величин. Следствие 2.Дисперсия суммы постоянной и св равна дисперсии св. Свойство 4. Дисперсия разности двух независ св равна сумме их дисперсий: D(X-Y)=D(X)+D(Y) Док-во: В силу третьего св-ва D(X-Y)=D(X)+D(-Y). По второму св-ву, D(X-Y)=D(X)+(-1)2*D(Y)=D(X)+D(Y). Линейная функция регрессии. Рассм 2мерн СВ(X,Y), где ХиУ-завис СВ. ] 1 из СВ явл функц от др. Огран-ся прибл предст, тк точное невозм. ] У- лин функц от Х. У Опр.: Функц У(х) наз сред кв регр у на х. Теор.: Лин сред кв регр у на х имеет вид
А прямую, соотв дан функц, наз прямой сред кв регр у на прямую ср кв регр х. Аналог,
Обе эти прямые проход через т. М(Х); М(У), кот наз центр совм распр СВ ХУ Случайные события: виды событий, действия над событиями. Свойства действий над событиями Под эксп-том или опытом или испытанием в т.в. понимается некая сов-ть действий, осуществляемых при строго фиксируемых и контролируемых усл-ях. Важной хар-кой эксп-та в т.в. явл. возм-ть его неоднокрю реализации, т.е. каждый эксп-т т.в. можно хотя бы в принципе повторить неск. раз.
Пространство элем. исходов (Ω)- мн-во, содерж. все возможные рез-ты данного случ. эксп-та, из кот. в эксп-те происходит ровно один. Элем-ты этого мн-ва- элементарные исходы (ωi). События-подмн-ва мн-ва Ω. Говорят, что в рез-те эксп-та произошло соб. А, если А принадл. Ω, т.е. если в эксп-те произошел один из элем. исходов, входящих в А. Виды соб-тий Достоверное соб- соб., кот обязательно произойдет а рез-те эксп-та, т.к. эт единств. соб, включ. все элем. исходы (Ω). Невозм. соб.- соб., кот. заведомо не может произойти, в рез-те эксп-та, т.е. это соб., не сод. ни одного элем. исхода (Ø). Заметим, что Ø принадл.Ω. Случ. соб.-соб, кот. в рез-те эксп-та может либо произойти, либо не произ. Действия над событиями
Свойства действий над соб. Законы де Моргана:
2. Частота и относительная частота события. Свойства относительной частоты. Вероятность случайного события. Связь между вероятностью и относительной частотой. Частота события Рассмотрим некот. опыт и связ. с ним случ. соб. А. Предположим, что опыт был повторен n раз, обозн. К -кол-во появл. А в опыте (абсолютная частота события). Очев, что К≤n, число Св-ва отн. частоты 1 2. 3. 4. Если A, B- несовм., то 5.Cвойство устойчивости частоты: если провести неск. серий из n испыт., то На основе данного св-ва можно сформировать статистическое определ. вер-ти: Если при большом числе испыт. А 1 2. 3. 4. Если A, B- несовм., то
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1080; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.71.237 (0.108 с.) |
 , если в рез-те эксп-та происх. либо соб. А, либо соб. В, либо оба. «+»= «или».
, если в рез-те эксп-та происх. либо соб. А, либо соб. В, либо оба. «+»= «или». , если в рез-те эксп-та наступили одновр. и соб. A и соб. В. «
, если в рез-те эксп-та наступили одновр. и соб. A и соб. В. «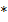 »= «и»
»= «и»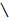 B)-соб., сост. в том, что произошло соб. А, но не произ. соб.В, т.е. A
B)-соб., сост. в том, что произошло соб. А, но не произ. соб.В, т.е. A  , сост. в невыполнении соб. А, т.е. мн-во элем.исходов соб.
, сост. в невыполнении соб. А, т.е. мн-во элем.исходов соб.  состоит из эл. исходов, не вход. в А.
состоит из эл. исходов, не вход. в А.  ), если всегда, когда происх. А, происх. В. Это означ., что любой элем. исх., вход. в А одновр. входит в В, т.е. А влечет В.
), если всегда, когда происх. А, происх. В. Это означ., что любой элем. исх., вход. в А одновр. входит в В, т.е. А влечет В. 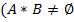 ). Аi, i=1…n образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие
). Аi, i=1…n образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие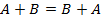




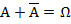









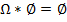




 =К/n –относит. частота соб. А.
=К/n –относит. частота соб. А. )=0
)=0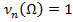


 в кажд.серии примет некотор. опред. знач., которое от серии к серии будет меняться. Однако, опыт показ, что при дост. большом знач. n
в кажд.серии примет некотор. опред. знач., которое от серии к серии будет меняться. Однако, опыт показ, что при дост. большом знач. n  будет сохр. почти пост. величину. Т.е. при росте n знач.
будет сохр. почти пост. величину. Т.е. при росте n знач.  колеблется около некоторого фикс. числа.
колеблется около некоторого фикс. числа. ). Дан. Вер-ть им. След. Св-ва:
). Дан. Вер-ть им. След. Св-ва: )=0
)=0
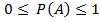

 , равноправны относительно попадания точки Т. Тогда за вероятность попадания точки Т в область А принимается отношение:
, равноправны относительно попадания точки Т. Тогда за вероятность попадания точки Т в область А принимается отношение: , где
, где  – геометрические меры областей А и
– геометрические меры областей А и 
 1/6 }
1/6 }








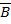 ,
, 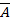 B, т.е. A+B= A
B, т.е. A+B= A  =AΩ=A(B+
=AΩ=A(B+  =BΩ=B(A+
=BΩ=B(A+  , а P(
, а P( ;
;  – формула Байеса. (P(A) находится по формуле полной вероятности)
– формула Байеса. (P(A) находится по формуле полной вероятности)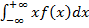

 или =
или =  = M(
= M( ) -
) - 

 свойства такие же, как для ДСВ
свойства такие же, как для ДСВ (X)= x max f(x)
(X)= x max f(x) , F(
, F( )=1/2
)=1/2







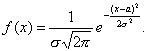
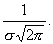
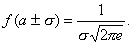








 , т.е. чем меньше рассеяние СВ Х вокруг ее М(Х), тем больше вероятность для СВ попасть в интервал от –
, т.е. чем меньше рассеяние СВ Х вокруг ее М(Х), тем больше вероятность для СВ попасть в интервал от –  . Если радиус интервала с центром в точке х=а взять равным 3
. Если радиус интервала с центром в точке х=а взять равным 3  , то почти все возможные значения СВ Х окажутся в этом интервале. Правило 3 сигма: если СВ распределена нормально, то абсолютная величина ее отклонения от М(Х) не превышает утроенного среднего квадратического отклонения
, то почти все возможные значения СВ Х окажутся в этом интервале. Правило 3 сигма: если СВ распределена нормально, то абсолютная величина ее отклонения от М(Х) не превышает утроенного среднего квадратического отклонения 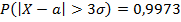
 У(х)=αX+β, где α и β -неизв параметры, кот мб найдены разл спос
У(х)=αX+β, где α и β -неизв параметры, кот мб найдены разл спос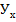 - М(У) = rху
- М(У) = rху  (Х-М(Х))
(Х-М(Х)) -коэф регр у на х.
-коэф регр у на х. - М(У) = rху
- М(У) = rху  (У-М(У))
(У-М(У)) -коэф регр х на у
-коэф регр х на у


