
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные незатухающие электромагнитные колебания в колебательном контуре.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Свободные незатухающие электромагнитные колебания можно получить в электрической цепи, состоящей из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R:
Свободные незатухающие электромагнитные колебания можно получить только в идеализированном случае, когда можно пренебречь электрическим сопротивлением (R 0) контура. Такие свободные незатухающие колебания называют еще собственными электромагнитными колебаниями. Можно доказать, что в колебательном контуре происходят гармонические колебания заряда, согласно закону:
или
где: q - мгновенное значение заряда конденсатора; q0 - амплитудное значение электрического заряда; w0 - собственная частота колебаний в контуре. Форма записи (через cos или sin) не имеет значения, так как отличие будет определяться лишь начальными условиями, а именно различной начальной фазой колебаний. Зная связь между зарядом конденсатора и разностью потенциалов на его обкладках:
можно аналогично записать гармонические колебания разности потенциалов:
или
где: U - мгновенное значение напряжения на обкладках конденсатора; U0 - амплитудное значение напряжения; w0 - собственная частота колебаний в контуре. Сила тока является первой производной от электрического заряда по времени:
Поэтому гармонические колебания силы тока в колебательном контуре будут происходить по закону:
где: i - мгновенное значение тока в контуре; J0 = q0 w0 - амплитудное значение тока; w0 - собственная частота колебаний в контуре. Циклическая частота w0 называется собственной частотой электромагнитных колебаний, она зависит только от параметров колебательного контура, а именно - от емкости конденсатора С и индуктивности L:
Период собственных электромагнитных колебаний, соответственно, вычисляется по формуле (Формула Томсона.):
Физические процессы, происходящие в колебательном контуре, сопровождается непрерывными преобразованиями одного вида энергии в другой, а именно: энергия электрического заряда конденсатора превращается в энергию магнитного поля катушки и наоборот. При этом, в полном соответствии с законом сохранения и превращения энергии, полная энергия в колебательном контуре остается величиной постоянной:
где: U и J - соответственно напряжение на обкладках конденсатора и сила тока в контуре в любой момент времени; U0 и J0 - амплитудные (максимальные) значения этих же величин. ПЕРИОД И ЧАСТОТА КОЛЕБАНИЙ. Важнейшей характеристикой механических, электрических, электромагнитных и всех других видов колебаний является период-время, в течение которого совершается одно полное колебание. Если, например, маятник часов-ходиков делает за 1 с два полных колебания, период каждого колебания равен 0,5 с. Период колебаний больших качелей - около 2 с, а период колебаний струны может быть от десятых до десятитысячных долей секунды. Другой величиной, характеризующей колебания, является частота (от слова "частое-число, показывающее, сколько полных колебаний в секунду совершают маятник часов, звучащие тела, ток в проводнике и т. п. Частоту колебаний оценивают единицей, носящей название герц (сокращенно пишут: Гц): 1 Гц-это одно колебание в 1 с. Если, например, звучащая струна совершает 440 полных колебаний в 1 с (при этом она создает тон "ля" первой октавы), говорят, что частота ее колебаний 440 Гц. Частота переменного тока электроосветительной сети 50 Гц. При таком токе электроны в.проводниках в течение 1 с текут попеременно 50 раз в одном направлении н столько же раз в обратном, т. е. совершают за 1 с 50 полных колебаний. Более крупные единицы частоты-килогерц (пишут: кГц), равный 1000 Гц, и мегагерц (пишут: МГц), равный 1000 кГц, или 1000000 Гц.
Вынужденные электромагнитные колебания. Установившиеся вынужденные электромагнитные колебания. Дифференциальное уравнение вынужденных колебаний и его решение методом векторных диаграмм. Явление резонанса. Резонанс токов и напряжений. Вынужденные колебания. Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь. Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω0. Если частота ω0 свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника. Для установления стационарных вынужденных колебаний необходимо некоторое время Δt после включения в цепь внешнего источника. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи. Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока. Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1):
где Рисунок 2.3.1. Вынужденные колебания в контуре Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому закон Ома можно записать для мгновенных значений токов и напряжений:
Величина Уравнение вынужденных колебаний можно записать в виде
где uR(t), uC(t) и uL(t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами UR, UC и UL. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм. На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов (рис. 2.3.2).
Изображение гармонических колебаний A cos (ωt + φ1), B cos (ωt + φ2) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме Длины векторов на диаграмме равны амплитудам колебаний A и B, а наклон к горизонтальной оси определяется фазами колебаний φ1 и φ2. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ1 – φ2. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов: Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи. Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору емкости C и катушки индуктивности L. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока. Резонанс Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов). При последовательном резонансе (ω = ω0) амплитуды UC и UL напряжений на конденсаторе и катушке резко возрастают:
Было введено понятие добротности RLC-контура:
Рисунок 2.3.4. Резонансные кривые для контуров с различными значениями добротности Q. Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC напряжения на конденсаторе к амплитуде
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.140 (0.007 с.) |

 Такую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими.
Такую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими. , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4)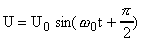 , (5)
, (5) . (6)
. (6) , (7)
, (7) . (8)
. (8) . (9)
. (9) , (10)
, (10)
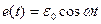
 0 – амплитуда, ω – круговая частота.
0 – амплитуда, ω – круговая частота.
 – это перенесенная с изменением знака из правой части уравнения в левую ЭДС самоиндукции катушки. Эту величину принято называть напряжением на катушке индуктивности.
– это перенесенная с изменением знака из правой части уравнения в левую ЭДС самоиндукции катушки. Эту величину принято называть напряжением на катушке индуктивности.
 Рисунок 2.3.2.
Рисунок 2.3.2.


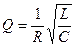
 Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.
Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.


