Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графоаналитические методы обработки опытных данныхСтр 1 из 2Следующая ⇒
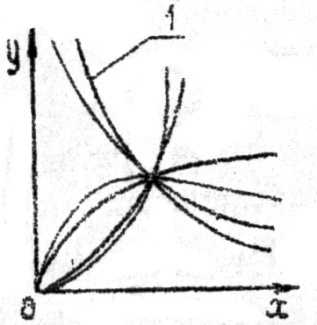
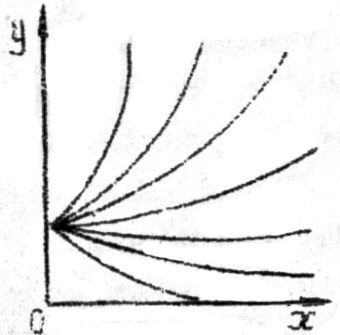
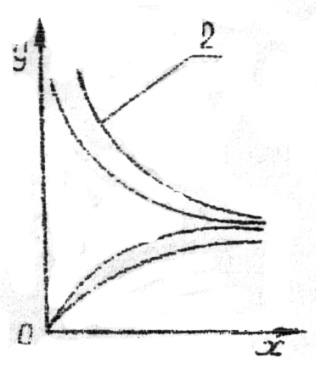
Это наиболее простые, наглядные и достаточно точные методы. В их основе лежат графические зависимости, представленные в виде прямых или кривых линий, проведенных по опытным точкам. При этом следует отчётливо представлять, что математическая обработка результатов наблюдений не может оставить перед собой задачу разгадать истинный характер зависимости между имеющимися переменными. Речь лишь идёт о том, чтобы охватить результаты опыта наиболее простой формулой, которая давала бы возможность производить интерполирование. Выбор типа эмпирической формулы производят, сравнивая кривую, построенную по данным наблюдений / эксперимента/, с типично графиками формул. В табл.1 графически представлены некоторые типы функций, наиболее часто встречающиеся при расчётах тепломассообменной аппаратуры пищевых производств. Для каждого семейства кривых дано исходное уравнение, метод его линеаризации и уравнение, полученное после линеаризации. Из таблицы видно, что иногда эмпирическая кривая похожа на несколько кривых, уравнения которых различны, например, кривая 1 и 2, поэтому, прежде чем определить численные значения коэффициентов в выбранной эмпирической формуле, необходимо проверить возможность её использования методом выравнивания (линеаризации). Метод выравнивания заключается в преобразовании функции Y=f(X) таким образом, чтобы превратить её в линейную функцию. Достигается это путём замены переменных x,y новыми переменными X=Ψ /x, y/, Y=ζ / x, y/ которые выбираются так, чтобы получилось уравнение прямой линии Y = A + BX Вычислив значения Xі Yi по заданным xi yi, наносят их на прямоугольную систему координат X Y. Если построенные таким образом точки располагаются вблизи прямой, то выбранная эмпирическая формула y= φ/X/ подходит для характеристики зависимости y=f/x/. Таблица 2
Особенно часто используются различные логарифмические сетки, с помощью которых можно «выпрямлять» графики степенных и показательных функций. В самом деле, если зависимость между x и y задаётся уравнением
y=aebx, (1) то логарифмирование его даёт lg y=/ b lg e/ x+ lg a (2) Полагая lg y=Y, lg a=A, b lg e = B, запишем уравнение (2) как Y= A+Bx (3) Из него видно, что оставив равномерную шкалу по оси ОХ и построив на оси ОУ логарифмическую шкалу, функция (1) изобразится прямой линией. Описанная выше сетка называется полулогарифмической. Логарифмической называется функциональная сетка, у которой на каждой из осей ОХ и ОУ построена логарифмическая шкала. На такой сетке графики степенных функций (кривые параболического и гиперболического вида) изобразятся прямыми линиями. Действительно, если y= axb (4) то lgy=lga+ b lgX (5) Полагая теперь lgy=Y, lga=A, lgx=X, запишем уравнение (5) в виде Y=A + BX, откуда и вытекает наше утверждение. Из сказанного вполне ясна роль функциональных сеток при обработке экспериментальных данных. Если результаты опытов, нанесённые в виде точек на обычных равномерных сетках, достаточно хорошо располагаются вдоль прямоё линии, то коэффициенты эмпирической формулы легко находятся, например, способом средних, либо графическим методом. Если же эти результаты располагаются вблизи кривой, то переведя полученные экспериментальные данные на ту или иную функциональную сетку, мы получаем возможность судить, на какой из них эти данные ближе всего подходят к прямой, а значит и о том, какую из формул следует выбрать для адекватного описания экспериментальных данных. 3.2.Определение коэффициентов, входящих в эмпирическую формулу . После того, как установлена пригодность выбранной формулы для выражения изучаемой зависимости переменных, необходимо определить численные значения входящих в формулу коэффициентов. Наиболее точные результаты даёт использование метода наименьших квадратов. Однако этот способ громоздок и во многих случаях его можно заменить более простым способом средних, дающих вполне удовлетворительные результаты. Способ средних заключается в следующем: использовав метод выравнивания и получив линейную зависимость Y = A + bX (6) составляют условные уравнения Yi = A + bXi, число которых равно числу имеющихся соответственных значений Xi, Yi. Условные уравнения разбивают на две приблизительно равные группы и уравнения, входящие в каждую из этих групп, складывают.
Получают два уравнения:
из которых находят неизвестные коэффициенты A и B. Наиболее простым способом получения коэффициентов эмпирических формул, однако, и наименее точным, является графический метод (метод натянутой нити). Он основан на геометрическом подборе прямой на глаз. С помощью соотвествующей замены линеаризуют функциональную зависимость и получают линейную функцию вида Y = A + BX Нанеся полученные экспериментальные значения на соответствующие функциональные шкалы, подбирают графически прямую(рис.2.), ближе всего подходящую к полученным значениям. Метод графического определения коэффициентов A и B понятен из рис.2. Графическое определение коэффициентов эмпирических формул
Рис.2. Обратный переход к исходной функциональной зависимости осуществляется с учётом использованного метода линеаризации. Если полученная прямая расположена далеко от начала координат и её невозможно продолжить (см. рис.2.), то используют следующие соотношения: A= B= где Y1 , X1, Y2 , X2 – численные значения координат двух произвольных точек полученной прямой. Рассмотрим теперь некоторые примеры применения этих двух способов. ПРИМЕР 1. В результате экспериментов получены значения перепадов давления DP, Па в функции от скорости воздуха Найти зависимость перепада давления от скорости воздуха. Таблица 3. Значение перепада давления DP в зависимости от скорости воздуха
По экспериментальным данным строим график (в обычных координатах), представленный на рис.3.
Зависимость перепада давления DP от скорости воздуха
Рис.3. Из сравнения полученной кривой с кривыми, приведёнными в табл.2., видно, что её можно аппроксимировать уравнением1, т.е. зависимость потери напора DP от скорости газа DP = a Обозначим Dp = y, lgy = lga + blgx (10) или Y = A + BX (11) В соответствии с уравнением (11) полученные экспериментальные данные изобразятся в логарифмических координатах в виде прямой, как это действительно видно из рис.4. Постоянные а и b определим графическим методом и методом средних. Зависимость перепада давления DP от скорости воздуха
Рис.4. Графический метод. Продолжив на рис.4. экспериментальную прямую до пересечения с осью координат, получим при X=0 значение a=0,112 (A=-0,951). Постоянную b (угловой коэффициент прямой) находят построением, показанием на рис.4 пунктирными линиями в соответствии с уравнением 8а. b=
Таким образом, при использовании графического метода получаем следующее уравнение
DP= 0.112 Метод средних. Подставим в уравнение (11) значения величин, соответствующих экспериментальным данным из таблицы 3, получим следующие уравнения: 0,4771 = A + 0,6998B 1.5378 = A + 1,2304B 0.7781 = A + 0,8512B 1.6627 = A + 1,2833B 1.0000 = A + 0,9590B 1.7781 = A + 1,3483B 1.1760 = A+ 1,0453B 1.0767 = A+ 1,3944B 1.3891 = A+ 1,1522B 1.9912 = A+ 1,4563B Разделив эти уравнения на две группы, и сложив уравнения каждой группы, получаем систему двух уравнений: 4,8203= 5A+4,7075B 8,8465=5A+6,7127B Решая её, получаем: B= b= 2 A= lga= -0,9158 = 1,0842; a= 0,1214 Подставив эти значения в уравнение (9), найдём выражение для определения потери напора в отверстиях ситчатой тарелки в зависимости от скорости воздуха в отверстиях P=0,1214 В правой части таблицы 3 приведены значения DP, вычисленные по эмпирическим уравнениям 12 и 13, а также отклонения расчётных значений величин в %, от значений полученных экспериментально. Как видно из таблицы 3, уравнение 13, полученное методом средних, является значительно более точным. ПРИМЕР 2. При конвективной сушке молочного сахара в псевдоожижённом состоянии получены следующие данные:
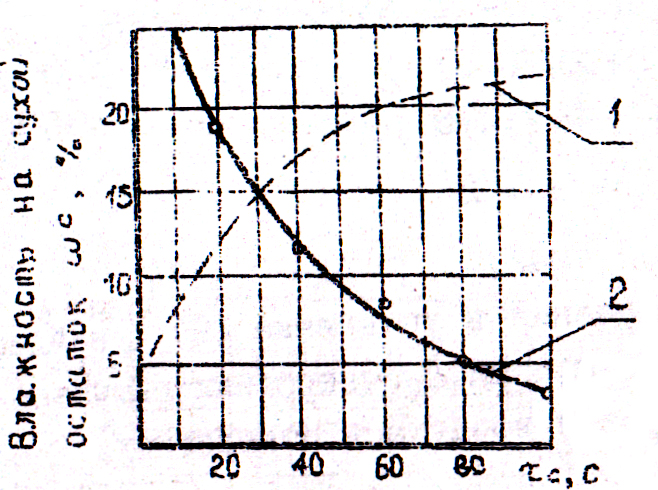
где τс – продолжительность сушки, с; ωс – влажность, рассчитанная на сухой остаток, %. Найти эмпирическую формулу, связывающую приведённые выше экспериментальные данные. Переводя полученные экспериментальные данные на простые прямоугольные координаты, по форме кривой мы получаем возможность подобрать функциональные шкалы(вид уравнения), в которых данные эксперимента расположатся вдоль прямой линии. То есть специальным подбором функциональных шкал исходный криволинейный график преобразуется к прямолинейному виду. На рис.5. изображён график зависимостиωс = f(τ с) (сплошная кривая) и экспоненциальная зависимость вида ωс = aenτ(штриховая кривая). Если опытные точки в простых координатах располагаются около монотонных кривых, изображенных на рис.5, которых не спрямляются в логарифмических координатах, то можно попытаться спрямить их а полулогарифмических координатах. В этом случае делается предположение, что искомая зависимость описывается уравнениями следующих видов: для кривой 1 ωс = a1еn1τ (14) для кривой 2 ωс = a2e-n2τ (15) График зависимости ωс = f(τ с) – кривая 2 (графическое изображение экспериментальных данных)
Рис.5. Уравнения вида 14, 15 обычно встречаются при описании различных тепло- и массообменных процессов, протекающих во времени. Рассматриваемый пример убедительно подтверждает справедливость поговорки: «Природа любит натуральный логарифм»
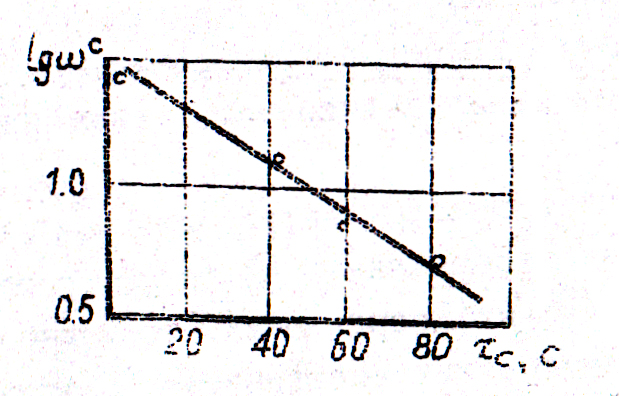
Кроме того, подобные монотонные кривые удобно описать зависимостью вида: Y= 10a+bx (16) Так как lgy= a+ bx(16а), то при наличии зависимости данного вида x и lgy связаны линейно, т.е. на полулогарифмической сетке (рис.6) зависимостью (16а) обращается в линейную. Полагая y= ωс, x= τ, найдём эмпирическую зависимость вида (16) Линеаризованный график уравнения (16) (кривая 2 на рис.5)
Рис.6. Пользуясь экспериментальными данными, составим табл.4.
В соответствии а прологарифмированным выражением (16), напишим уравнения 1,4698 = a + 0b 1,2648= a + 20b 1,0755= a + 40b 0,9031= a + 60b 0,6990= a + 80b 0,5185=a +100b Группируя уравнения по 3 в порядке проведения экспериментов, имеем 3,8101 = 3a+ 60b 2,1206 = 3a+ 240b Решая эти уравнения, получим a= 1,4568 b= -0,00938 Подставив полученные значения коэффициентов aи b в уравнение (16), получим следующую эмпирическую формулу ωс =101,4568-0,0938τ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 702; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.8.82 (0.058 с.) |
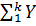 i=kA + B
i=kA + B 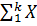 i;
i; 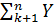 I = (n-k)A + B
I = (n-k)A + B 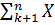 I (7)
I (7)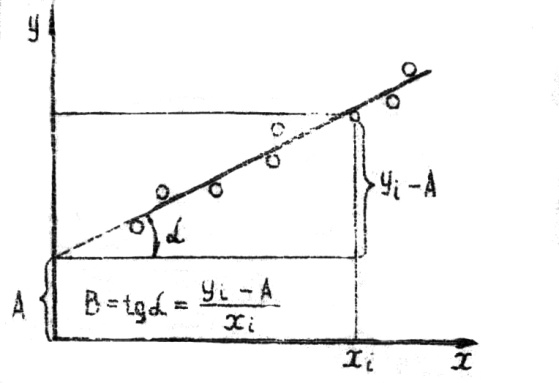
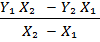 (8)
(8)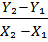 (8a)
(8a)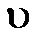 , м/с, в отверстиях ситчатой тарелки, приведённой в табл.3.
, м/с, в отверстиях ситчатой тарелки, приведённой в табл.3.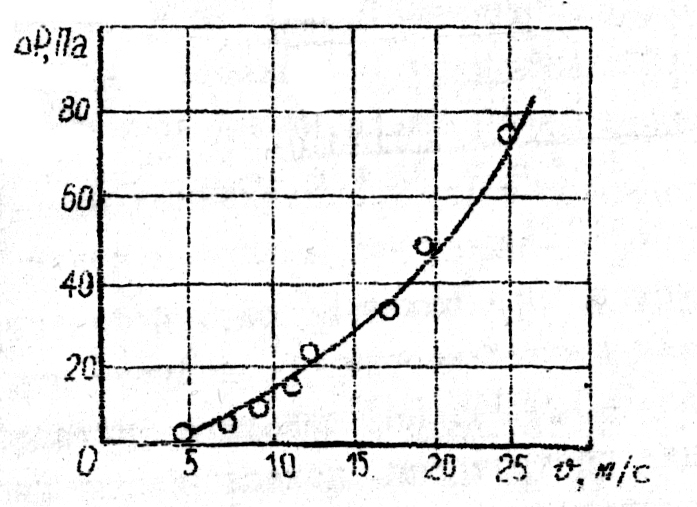
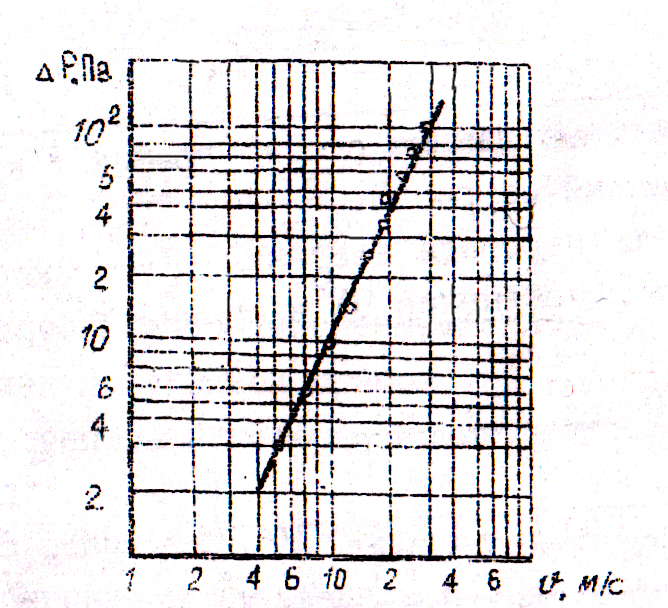
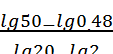 = 2.045
= 2.045