
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрична інтерпретація задачі лінійного програмування
Розглянемо на площині
Кожна нерівність цієї системи геометрично визначає півплощину з граничною прямою
Мал. 4.1. Сукупність цих точок (розв'язків) називають багатокутником розв'язків, або областю допустимих планів (розв'язків) задачі лінійногопрограмування. Це може бути точка (єдиний розв'язок), відрізок, промінь, багатокутник, необмежена багатокутна область. Якщо в даній системі обмежень буде три змінних, то кожна нерівність геометрично визначатиме півпростір тривимірного простору, граничними площинами якого будуть:
а умови невід’ємності — півпростори з граничними площинами Нехай у даній системі обмежень кількість змінних більша, ніж три: Якщо система обмежень сумісна, то за аналогією з тривимірним простором вона утворює спільну частину в Отже, геометрично задача лінійного програмування являє собою відшукання координат такої точки багатогранника розв'язків, при підстановці яких у цільову лінійну функцію остання набирає максимального (мінімального) значення, причому допустимими розв'язками є усі точки багатогранника розв'язків. Цільову функцію
Розглянемо геометричну інтерпретацію задачі лінійного програмування на прикладі. Задача 4.1. Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукрові буряки на площі 20 га, відвівши під цукрові буряки не менше як 5 га. Техніко-економічні показники вирощування цих культур маємо у табл. 4.1:
Таблиця 4.1.
Критерієм оптимальності є максимізація прибутку. Запишемо економіко-математичну модель структури виробництва озимої пшениці та цукрових буряків, ввівши такі позначення:
Задача лінійного програмування має такий вигляд:
Геометричну інтерпретацію задачі зображено на мал.4.2.
Мал. 4.2. Область допустимих розв’язків задачі Область допустимих розв’язків цієї задачі дістаємо так. Кожне обмеження, наприклад Основні властивості розв’язків задачі лінійного програмування. Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем. Теорема 4.1. Множина всіх планів задачі лінійного програмування опукла. Доведення. Необхідно довести, що коли
Так як
Якщо підставити в систему обмежень значення Х, то отримаємо: Отримали, що Х задовольняє систему обмежень задачі лінійного програмування (3.2), і оскільки Теорема 4.2. Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин багатогранника розв’язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин. Теорема 4.3. Якщо відомо, що система векторів
де всі Доведення. Припустимо, що точка Х не є кутовою. Тоді вона може бути виражена опуклою лінійною комбінацією двох інших точок
Компоненти векторів
Оскільки
Віднімаючи від першого рівняння друге, отримаємо:
За припущенням вектори
Звідки: Отже, Х неможливо подати як опуклу лінійну комбінацію двох інших точок багатокутника розв’язків. Значить, Х – кутова точка. Теорема 4.4. Якщо Наслідки: 1) Оскільки вектори 2) Кожній кутовій точці багатокутника розв’язків відповідає З наведених властивостей можна зробити наступні висновки: якщо функціонал задачі лінійного програмування обмежений на багатограннику розв’язків, то: 1) існує така кутова точка багатогранника розв’язків, в якій лінійний функціонал досягає свого оптимального значення; 2) кожний опорний план відповідає кутовій точці багатогранника розв’язків. Тому для розв’язання задачі лінійного програмування необхідно досліджувати лише кутові точки багатогранника (опорні плани), не включаючи до розгляду внутрішні точки множини допустимих планів.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.28.197 (0.015 с.) |
 сумісну систему лінійних нерівностей:
сумісну систему лінійних нерівностей:


 . Умови невід’ємності змінних визначають півплощини з граничними прямими
. Умови невід’ємності змінних визначають півплощини з граничними прямими 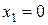 та
та  . Система сумісна, тому півплощини як опуклі множини, перетинаючись, утворюють спільну частину, що є опуклою множиною і являє собою сукупність точок, координати кожної з яких є розв'язком даної системи (мал. 4.1).
. Система сумісна, тому півплощини як опуклі множини, перетинаючись, утворюють спільну частину, що є опуклою множиною і являє собою сукупність точок, координати кожної з яких є розв'язком даної системи (мал. 4.1).
 ,
,  , де
, де  - номер обмеження, а
- номер обмеження, а  - номер змінної. Якщо система обмежень сумісна, то ці півпростори як опуклі множини, перетинаючись, утворять у тривимірному просторі спільну частину, що називається багатогранником розв'язків. Він може бути точкою, відрізком, променем, багатокутником, багатогранником, багатогранною необмеженою областю.
- номер змінної. Якщо система обмежень сумісна, то ці півпростори як опуклі множини, перетинаючись, утворять у тривимірному просторі спільну частину, що називається багатогранником розв'язків. Він може бути точкою, відрізком, променем, багатокутником, багатогранником, багатогранною необмеженою областю. ; тоді кожна нерівність визначає півпростір
; тоді кожна нерівність визначає півпростір  -вимірного простору з граничною гіперплощиною
-вимірного простору з граничною гіперплощиною  ,
,  .
. в
в  — шукана площа посіву озимої пшениці, га;
— шукана площа посіву озимої пшениці, га; — шукана площа посіву цукрових буряків, га.
— шукана площа посіву цукрових буряків, га. за умов:
за умов:

 , задає півплощину з граничною прямою
, задає півплощину з граничною прямою 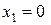 і
і  являє собою сім’ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z = 0, то маємо
являє собою сім’ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z = 0, то маємо  . Ця пряма проходить через початок системи координат. Коли Z = 3,5, то маємо пряму
. Ця пряма проходить через початок системи координат. Коли Z = 3,5, то маємо пряму  .
. та
та  - плани задачі лінійного програмування (3.1)-(3.3), то їх опукла комбінація
- плани задачі лінійного програмування (3.1)-(3.3), то їх опукла комбінація  також є планом задачі.
також є планом задачі.
 .
. то й
то й  , тобто задовольняють і умову (3.3). У такий спосіб доведено, що Х – план задачі лінійного програмування.
, тобто задовольняють і умову (3.3). У такий спосіб доведено, що Х – план задачі лінійного програмування. у розкладі
у розкладі  лінійно незалежна і така, що
лінійно незалежна і така, що
 , то точка
, то точка 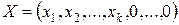 є кутовою точкою багатогранника розв’язків.
є кутовою точкою багатогранника розв’язків. та
та  невід’ємні і останні n-k компонентів вектора Х дорівнюють нулю, тому відповідні n-k компонент векторів
невід’ємні і останні n-k компонентів вектора Х дорівнюють нулю, тому відповідні n-k компонент векторів  ,
,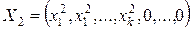 .
. ,
,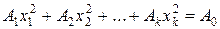 .
.
 лінійно незалежні, тому останнє співвідношення виконується, якщо
лінійно незалежні, тому останнє співвідношення виконується, якщо
 .
. - кутова точка багатогранника розв’язків, то вектори в розкладі
- кутова точка багатогранника розв’язків, то вектори в розкладі  , є лінійно незалежними.
, є лінійно незалежними. мають розмірність m, то кутова точка багатокутника розв’язків має не більше, ніж m додатних компонентів
мають розмірність m, то кутова точка багатокутника розв’язків має не більше, ніж m додатних компонентів  .
. лінійно незалежних векторів системи
лінійно незалежних векторів системи 


