
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная. Теорема о связи двух первообразных. Свойства неопределённого интеграла.Стр 1 из 3Следующая ⇒
Первообразная. Теорема о связи двух первообразных. Свойства неопределённого интеграла. Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого Т. Если F1(x) и F2(x) - первообразные для одной и той же функции f(x), то их разность есть величина постоянная. Свойства: а) Если функция f (x) имеет первообразную на промежутке X, и k – число, то б) Если функции f (x) и g (x) имеют первообразные на промежутке X, то в) Если функция f (x) имеет первообразную на промежутке X, то для внутренних точек этого промежутка: г) Если функция f (x) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
Интегрирование по частям. Если функции u (x) и v (x) имеют непрерывные первые производные и существует интеграл v (x) du(x), то существует и интеграл u (x) dv (x) и имеет место равенство: u (x) dv (x) = u (x) • v (x) – v (x) du (x) или в более короткой форме: u dv = u v – v du. Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями.
Интегрирование дробно-рациональных выражений.
Понятие определённого интеграла. Геометрический смысл определённого Интеграла. Число J называется определенным интегралом от функции f (x) на отрезке [a; b], если для любого ε > 0 существует такое Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x) и прямыми у=0; х=а; х=b. Свойства определённого интеграла.
а) Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. б) Определенный интеграл с одинаковыми пределами интегрирования равен нулю в) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный. г) Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам. д) Постоянный множитель можно выносить за знак определенного интеграла. е) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций. Теорема о среднем значении (док-во). Если f(x) - непрерывная функция, заданная на промежутке [a, b], то существует такая точка Так как при всех k будет m ≤ f(ξk) ≤ M, а xk+1 > xk, то m(xk+1 - xk) ≤ M(xk+1 - xk). Складывая такие неравенства и замечая, что
Однородные ОДУ. Уравнение вида
Линейные ОДУ. Под линейным ОДУ первого порядка понимают уравнение, которое является линейным по отношению к неизвестной функции и ее производной:
Уравнение Бернулли.
Обыкновенные дифференциальные уравнения (ОДУ) 1-ого порядка Если пользоваться другим обозначением производной, то можно записать (6) как Общее решение (общий интеграл) уравнения при n = 1 имеет вид
Первообразная. Теорема о связи двух первообразных. Свойства неопределённого интеграла. Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого Т. Если F1(x) и F2(x) - первообразные для одной и той же функции f(x), то их разность есть величина постоянная. Свойства: а) Если функция f (x) имеет первообразную на промежутке X, и k – число, то б) Если функции f (x) и g (x) имеют первообразные на промежутке X, то в) Если функция f (x) имеет первообразную на промежутке X, то для внутренних точек этого промежутка: г) Если функция f (x) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
Интегрирование по частям. Если функции u (x) и v (x) имеют непрерывные первые производные и существует интеграл v (x) du(x), то существует и интеграл u (x) dv (x) и имеет место равенство: u (x) dv (x) = u (x) • v (x) – v (x) du (x) или в более короткой форме: u dv = u v – v du. Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.121.131 (0.011 с.) |

 Так, функция
Так, функция  является первообразной функции
является первообразной функции  в чем можно убедиться, поставив эти функции в определение первообразной. Функция
в чем можно убедиться, поставив эти функции в определение первообразной. Функция  также является первообразной функции
также является первообразной функции  Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f.
Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f. (постоянную можно выносить за знак интеграла)
(постоянную можно выносить за знак интеграла) (интеграл суммы равен сумме интегралов)
(интеграл суммы равен сумме интегралов) (производная от интеграла равна подынтегральной функции)
(производная от интеграла равна подынтегральной функции)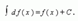 (интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования)
(интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования)
 что для разбиения отрезка [a; b] на равные части n точками и для любого выбора точек
что для разбиения отрезка [a; b] на равные части n точками и для любого выбора точек 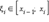 выполняется неравенство
выполняется неравенство 
 , где х, t – любые буквы.
, где х, t – любые буквы. .
.



 , что
, что 
 (14). В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму
(14). В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму 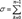



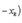
 , получим m(b - a) ≤ σ ≤ M(b - a). Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству
, получим m(b - a) ≤ σ ≤ M(b - a). Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству 

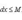 Таким образом, частное
Таким образом, частное 
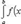
 есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14). Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a> b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b.
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14). Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a> b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b. Заменой z = y/x это уравнение сводится к уравнению с разделяющимися переменными относительно функции z = z(x)
Заменой z = y/x это уравнение сводится к уравнению с разделяющимися переменными относительно функции z = z(x) 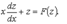
 в данном случае
в данном случае 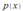 и
и  представляют собой заданные непрерывные функци от х или являются постоянными. Y=U*V – сводится к 2 ур. с разделенными переменными.
представляют собой заданные непрерывные функци от х или являются постоянными. Y=U*V – сводится к 2 ур. с разделенными переменными. , y=U*V. В рез-те замены данное уравнение сводится к 2.
, y=U*V. В рез-те замены данное уравнение сводится к 2.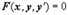 где x - независимая переменная, y(x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:
где x - независимая переменная, y(x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так: 

 или
или  .
.


