Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы умножения и их структурные проекции.Стр 1 из 3Следующая ⇒ Системы умножения и их структурные проекции. Гармоничные фигуры и их проекции.
Гармоничная фигура одномерного пространства.
В одномерном пространстве любая фигура (структура) будет иметь две опорные точки. Данное утверждение легко визуально проверить – достаточно нарисовать на поверхности листа бумаги (двухмерного пространства) любую фигуру, затем повернуть лист ребром к наблюдателю. Если толщиной листа пренебречь, то мы получим одномерное пространство с нарисованной нами фигурой, которая будет выглядеть как отрезок. Любой отрезок будет всегда иметь две опорные точки. Данное утверждение можно записать следующим образом:
| a |1 = 2
Иначе говоря, для определения какой-либо структуры спроектированной на одномерное пространство необходимо определить две ее опорные точки.
Гармоничная фигура двухмерного пространства.
Для получения гармоничной структуры двухмерного пространства необходимо провести перпендикуляр к одномерной фигуре (проекции структуры на одномерном пространстве) на длину самой фигуры, т.е. одномерная фигура «двигается» на длину самой себя по вектору являющемся перпендикуляром к ней. Оставленный при движении «след» и будет являться гармоничной фигурой двухмерного пространства.
Получившаяся гармоничная фигура двухмерного пространства будет являться квадратом и соответственно иметь четыре опорные точки т.е.:
| а | 2 = 4
Гармоничная фигура трехмерного пространства. При увеличении мерности пространства на единицу гармоничная фигура получается путем проекции гармоничной фигуры предыдущей мерности на ее же длину по вектору являющимся перпендикуляром к ней и к векторам измерения предыдущей мерности, т.е.:
Согласно данному правилу, для получения гармоничной фигуры трехмерного пространства необходимо осуществить проекцию (движение) гармоничной фигуры двухмерного пространства на длину самой себя по вектору являющемуся перпендикуляром к векторам измерения мерности двухмерного пространства, т.е.:
Получившийся при проекции объемный след будет являться гармоничной фигурой трехмерного пространства, т.е. кубом и иметь уже восемь опорных точек.
Гармоничная фигура четырехмерного пространства.
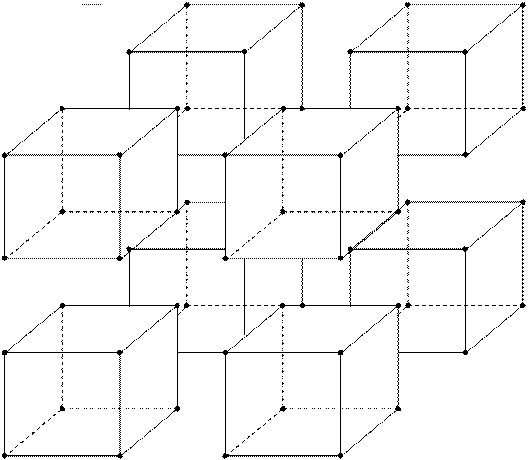
Аналогичным образом получаются гармоничные фигуры следующих измерений. К примеру, что бы получить гармоничную фигуру четырехмерного пространства необходимо осуществить проекцию гармоничной фигуры трехмерного пространства – куба на длину самого куба по вектору являющимся перпендикуляром к векторам измерений трехмерного пространства т.е.:
На плоскости это можно изобразить следующим образом (для удобства восприятия углы отмечены цифрами):
Отобразив куб таким образом, мы фактически осуществили сдвиг его по времени и получили гармоничную четырехмерную фигуру, которая имеет шестнадцать опорных точек, т.е.:
По данной аналогии легко выстраиваются гармоничные фигуры следующих порядков мерности их пространств.
Гармоничная фигура пятимерного пространства.
Гармоничная фигура шестимерного пространства.
Таблица соответствий гармоничных фигур разномерных пространств с количеством их опорных точек.
Триадные системы.
Х’Арийские таблицы умножения Гармоничная система умножения
Триадная система умножения.
Триадная система умножения при вычислении использует структуры малой и трехмерной триад:
- малая триада (основание - 3)
-
Двухмерное триадное умножение.
Малая триада при данном умножении указывает на структуру, построение формы которой используется при вычислении. При двухмерных триадных вычислениях, в качестве первого множителя, используется знак двухмерной триады - Zили z. Второй множитель указывает на количество рядов в триаде. Результатом же является количество точек в получившейся триаде.


Z * 6 \ Z6 = 21
Z * 8 \ Z8 = 32 Z * 9 \ Z9 = 41 Z * 10 \ Z10 = 51 Z * 11 \ Z11 = 66 Z * 12 \ Z12 = 78 Z * 13 \ Z13 = 91 Z * 14 \ Z14 = 105 Z * 15 \ Z15 = 120 Z * 16 \ Z16 = 136
Трехмерное триадное умножение.
При трехмерных триадных вычислениях, в качестве первого множителя, используется знак объемной триады - eили знак z, если задано трехмерное умножение знаком ЖДЫ (&). Второй множитель указывает на количество рядов в триаде. Результатом является количество точек в получившейся триаде.
  z & 3 \ e2 = 10 z & 3 \ e2 = 10
en ≡ en-1 + Zn
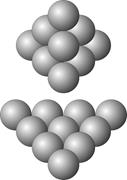
Дело в том, что трехмерная триада состоит из соединенных между собой плоскостями малыми триадами, у которых длины сторон увеличиваются на единицу по порядку возрастания номеров рядов в трехмерной триаде (если рядом номер один считать самый верхний ряд). Например структура трехмерной триады сформированная умножением триадно жды три (e3 ) состоит из следующих малых триад:
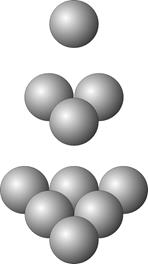
Ряд №1 = 1
Ряд №2 - Z2 = 3
Ряд №3 - Z3 = 6
Триадно жды четыре получается путем «добавления снизу» еще одной малой триады, длина стороны которой будет уже равна четырем, т.е.:
Если при вычислении таблиц трехмерного триадного умножения не брать в расчет таблицы двухмерного умножения, то путем нехитрых вычислений можно получить еще одну формулу:
en ≡ en-1 - en-2 + en-1 + n
Например:
e5 ≡ e5-1 - e5-2 + e5-1 + 5 = e4 - e3 + e4 + 5 = 20 – 10 + 20 + 5 = 35
Ровная система умножения
Данная система так называется от понятия «Ровна» т.е. равномерная структура, где количество точек по любым направлениям равны между собой. Существуют следующие виды Ровны: 1)
 Малая Ровна Малая Ровна
2)
 Трехмерная Ровна Трехмерная Ровна
Умножение Малой Ровны
Результат данного умножения определяется суммой точек в малой Ровне, причем второй множитель показывает количество рядов точек в обеих сторонах Ровны.
 y * 2 \ Y 2 = 4 y * 2 \ Y 2 = 4
y * 4 \ Y 4 = 16
Явно видно, что результат умножения «ровно на …» получается путем плоскостного умножения второго множителя на самого себя, т.е.:
Yn \ n * n
Умножение Трехмерной Ровны
 y & 2 \ E2 = 8 y & 2 \ E2 = 8
 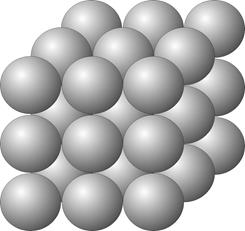 y & 3 \ E3 = 27 y & 3 \ E3 = 27
y & 4 \ E4 = 64
Результат умножения «ровно ЖДЫ …» получается путем плоскостного умножения второго множителя на самого себя со степенью повторений умножения равного самому себе, т.е.:
или, говоря языком «стандартной математики», результат возведения в куб (n3) множителя ровно жды и будет результатом данного умножения.
Пример решения арифметического действия:
т.к. после ровно жды не указан какой-либо множитель, то подразумевается изначальная структура Трехмерной Ровны т.е. E2.
Пядевая система мер
Пядевая система мер существовала еще до привязки ее к человеческому организму. Основу данной системы мер составляет пядь: ç p
p (пядь) равна 17,78 см, что примерно составляет расстояние от конца большого пальца до конца указательного при их разведения в стороны. Для обозначения мерности над знаками ставится специальный указатель, означающий, что данное обозначение определяет длину чего-либо, например пядь указывающая на длину изображается следующим образом: q Для обозначения простой цифирности также применяется специальный знак, например числовое обозначение «тьмы» (10.000) выглядит следующим образом: U В пядевой системе мер существуют следующие основные группы величин: - основные малые меры; - основные средние меры; - основные большие меры.
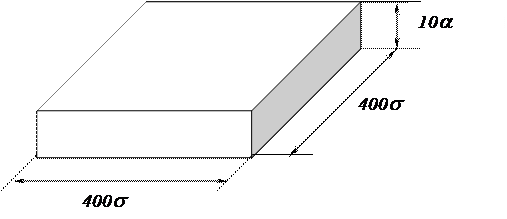
Задача №1. Для постройки Святилища необходимо заложить равносторонний фундамент площадью (Sф) круг темных саженей (16 темных саженей, т.е. kUs), высотой (Hф) 10 аршин (10a). Рассчитать сколько необходимо блоков для фундамента, если имеющиеся блоки имеют следующие размеры: Lб, длина – 20 саженей (20s); Hб, ширина – 2 аршина (2a); Bб, высота – 1 сажень (s).
Решение: Sф = kUs = 16 * 10 000 * s = 160 000s = 400 * 400 s
Hф / Hб = 10a / 2a = 5 – рядов блоков может быть помещено по высоте в фундаменте.
Lф / Lб = 400s / 20s = 20 – рядов блоков в фундаменте по длине.
Bф / Bб = 400s / 1s = 400 – рядов блоков в фундаменте по ширине.
N = 5 * 20 * 400 = 40.000 шт.
Задача для самостоятельного решения: Капище – хранилище было высотой 27s и имело оно вид пятиугольника, где на кубе со стороной 12s покоилась пирамида. Внутреннее пространство Капища было разделено на 4 равные комнаты. Толщина стен Капища (что внутри, что снаружи) равна 1m, дверные проемы были 2a в ширину и 1,2s в высоту. Сколько необходимо гранитных блоков для строительства Капища – хранилища, если они имеют следующие размеры: ширина – 2L, длина - s, высота - c. Славянские меры времени
Сутки в славянской системе имеют обозначение - A. 365 суток составляют одно лето - N. В Священном лете 369 суток - O.
N = 365A O = 369A
Сутки состоят из 16 часов - F. Час состоит из 144 частей - G. Часть состоит из 1296 долей - H. Доля состоит из 72 мгновений - I. Мгновение состоит из 760 мигов - J. Миг состоит из 160 сигов - K.
A = 16 F
F = 144 G
G = 1296H
H = 72 I
I = 760 J
J = 160 K
Для сравнения славянской системы меры времени и современной системы можно произвести следующий расчет:
В сутках согласно современному времяисчислению – 24 часа. В сутках согласно славянским мерам времени – 16 часов, соответственно получается следующая пропорция:
т.е. за 5 минут «современного времени» проходит 8 частей славянского. При различных расчетах со временем, получающиеся коэффициенты смещения выражаются в:
Системы умножения и их структурные проекции.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.112.82 (0.008 с.) |
 мерность пространства, которым ограничена структура
мерность пространства, которым ограничена структура какая-либо структура
какая-либо структура

 | a | 2 ≡ | a | 1 | a | 1 ≡ 4
| a | 2 ≡ | a | 1 | a | 1 ≡ 4

 | a | N ≡ | a | N-1 | a | N-1
| a | N ≡ | a | N-1 | a | N-1 | a | 3 = | a | 2 | a | 2
| a | 3 = | a | 2 | a | 2


 | a | 3 ≡ | a | 2 | a | 2 ≡ 8
| a | 3 ≡ | a | 2 | a | 2 ≡ 8 | a | 4 = | a | 3 | a | 3
| a | 4 = | a | 3 | a | 3 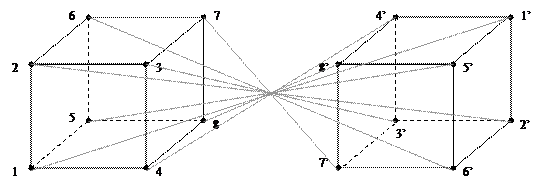
 | a | 5 ≡ | a | 4 | a | 4 ≡ 32
| a | 5 ≡ | a | 4 | a | 4 ≡ 32

 | a |2
| a |2
 | a |7
| a |7

 трехмерная триада (основание - 4)
трехмерная триада (основание - 4)




 Z * 2 \ Z2 = 3
Z * 2 \ Z2 = 3





 Z * 3 \ Z3 = 6
Z * 3 \ Z3 = 6
 Z * 7 \ Z7 = 28
Z * 7 \ Z7 = 28


 z & 2 \ e2 = 4
z & 2 \ e2 = 4




 В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:
В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:















 Результат этого умножения определяется суммой точек в трехмерной Ровне. Второй множитель показывает количество рядов точек во всех трех сторонах Ровны.
Результат этого умножения определяется суммой точек в трехмерной Ровне. Второй множитель показывает количество рядов точек во всех трех сторонах Ровны.





 En \ n * |n|n
En \ n * |n|n

 Y * 3 + E = 9 + E = 9 + 8 = 17
Y * 3 + E = 9 + E = 9 + 8 = 17