
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Екстремуми функції двох змінних (необхідні умови екстремуму).
Функція z = f (x,y) має максимум (мінімум) в точці Максимум або мінімум функції називається її екстремумом. Точка Якщо диференційована функція z = f (x,y) досягає екстремуму в точці Точки, в яких частинні похідні дорівнюють нулю, називаються стаціонарними точками функції. Не всі стаціонарні точки є точками екстремуму. Нехай якщо якщо якщо Схема дослідження функцій z = f (x,y) на екстремум При дослідженні функцій z = f (x,y) на екстремум (при умові, що вона двічі диференційована) користуються правилом: 1.Знаходяться частинні похідні першого порядку функції z = f (x,y) і розв’язують систему рівнянь:
Точки, в яких частинні похідні дорівнюють нулю, називаються стаціонарними точками. Нехай одна з них 2. Знаходять частинні похідні другого порядку та мішані функції z = f (x,y) і обчислюють їх значення в точці Позначимо 3. Обчислюють визначник
Якщо виявляється, що Задача 2. Знайти екстремум заданої функції а) б)
Теоретичні відомості про градієнт функції Похідна за даним напрямком. Градієнт функції. Означення. Похідною функції z = f (x,y) в точці
Якщо функція f (x,y) диференційована, то похідна за даним напрямком визначається за формулою: Градієнтом функції z = f (x,y) в точці
Градієнт вказує напрям найшвидшого зростання функції в даній точці. Похідна
Задача 3. Знайти похідну функції Задача 4. Мале підприємство виробляє товари А і В. Загальні щоденні витрати V (в гривнях) на виробництво x одиниць товару А та y одиниць товару В відомі:
1. Означення функції двох змінних (трьох та більшого числа змінних). 2. Неперервність функції. 3. Частинні похідні функції двох змінних. 4. Частинні похідні другого порядку. Мішані частинні похідні.
7. Правило дослідження функції двох змінних на екстремум. Висновок __________________________________________________________ ____________________________________________________________________________________________________________________________________
Перевірив викладач________Оцінка___________Дата_________
ТЕМА 6. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ПРАКТИЧНА РОБОТА № 13 Тема. Розв’язування задач на обчислення невизначених інтегралів частинами та заміною змінних Мета роботи: Навчитись обчислювати невизначені інтеграли частинами та заміною змінних. Наочне забезпечення та обладнання: 1. Інструкційні картки 2. Приклади задач 3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування”, “Властивості невизначеного інтегралу”. 4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про невизначений інтеграл та методи інтегрування Означення. Функція F (x) називається первісною для функції f (x), якщо f ¢(x)= F (x). Означення. Невизначеним інтегралом від функції f (x) називається сукупність усіх первісних цієї функції. Використовується позначення З геометричного погляду невизначений інтеграл – це сукупність (сім’я) ліній F (x)+ C
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.8.247 (0.033 с.) |
 , якщо значення в цій точці більше (менше), ніж її значення в будь – якій іншій точці
, якщо значення в цій точці більше (менше), ніж її значення в будь – якій іншій точці 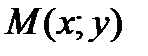 деякого околу точки
деякого околу точки  , тобто
, тобто  (відповідно
(відповідно  ) для всіх точок
) для всіх точок  , де
, де  - достатньо мале число.
- достатньо мале число. ;
; 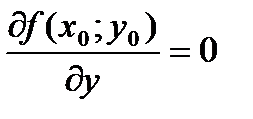 .
. ;
;  ;
;  .Складемо дискримінант
.Складемо дискримінант  . Тоді:
. Тоді: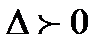 , то функція в точці
, то функція в точці  (або
(або  ) і мінімум при
) і мінімум при 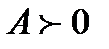 (або
(або  );
); , то в точці
, то в точці 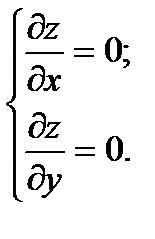
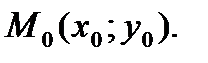
 ;
;  ;
;  .
. .
. то функція z = f (x,y) в точці
то функція z = f (x,y) в точці  і мінімум при
і мінімум при  . Якщо ж
. Якщо ж  то в точці
то в точці 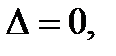 то питання про екстремум в цій точці залишається відкритим і вимагає додаткового дослідження.
то питання про екстремум в цій точці залишається відкритим і вимагає додаткового дослідження.


 =
=  називається границя
називається границя  , де
, де 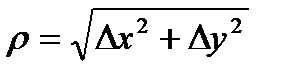 .
. , де
, де  - кут, утворений вектором
- кут, утворений вектором  .
. . Градієнт функції і похідна за напрямком вектора
. Градієнт функції і похідна за напрямком вектора 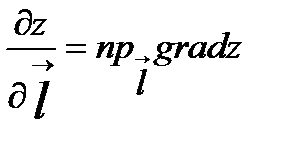 .
. за напрямком градієнта має найбільше значення, що дорівнює:
за напрямком градієнта має найбільше значення, що дорівнює: .
. в точці M(3;4) за напрямком градієнта функції z.
в точці M(3;4) за напрямком градієнта функції z. . Визначити кількість одиниць товарів А і В, яку потрібно виробляти, щоб загальні витрати підприємства були мінімальними.
. Визначити кількість одиниць товарів А і В, яку потрібно виробляти, щоб загальні витрати підприємства були мінімальними. Питання для самоконтролю знань, умінь.
Питання для самоконтролю знань, умінь.
 ,де f (x) dx - підінтегральний вираз, а C - стала інтегрування.
,де f (x) dx - підінтегральний вираз, а C - стала інтегрування.


