
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальна характеристика засобів рішення задач нелiнійного програмування
Коли цільова функція (5.6) і обмеження (5.7) нелінійні та для пошуку точки екстремуму не можна або дуже складно використовувати аналітичні засоби рішення, тоді для рішення задач оптимізації застосовуються засоби нелiнійного програмування. Як правило, при рішенні задач засобами нелінійного програмування використовуються численні засоби з застосуванням ЕОМ. В основному засоби нелiнійного програмування можуть бути охарактеризовані як багатокрокові засоби чи засоби наступного поліпшення вихідного рішення. У цих задачах звичайно заздалегідь не можна сказати, яке число кроків гарантує знаходження оптимального значення з заданою мірою точності. Крім того, у задачах нелiнійного програмування вибір величини кроку представляє серйозну проблему, від успішного рішення якої залежить ефективність застосування того чи іншого засобу. Розмаїтість засобів рішення задач нелiнійного програмування якраз і пояснює прагнення знайти оптимальне рішення за найменше число кроків. Більшість засобів нелiнійного програмування використовують ідею руху у n-мірному просторі в напрямку оптимуму. При цьому із деякого вихідного чи проміжного стану Uk здійснюється перехід в наступний стан Uk+1 зміною вектору Uk на величину ΔUk, що називається кроком, тобто: Uk+1=Uk+ΔUk (5.26).
В ряді засобів крок, тобто його величина і напрямок визначається як деяка функція стану Uk: ΔUk=f(Uk) (5.27)
Отже, згідно з (5.26) новий стан Uk, що одержується внаслідок виконання кроку (5.27) може розглядатися як функція вихідного стану
Uk+1=Uk+f(Uk). (5.28)
У деяких засобах ΔUk зумовлено не тільки станом Uk, але і рядом попередніх станів:
ΔUk=f(Uk),Uk-1…,Uk-2 (5.29)
Uk+1=Uk+f(Uk),Uk-1…,Uk-2. (5.30)
Природно, що алгоритми пошуку типу (5.30) є більш загальними і принципово спромагаються забезпечити більш високу сходимість до оптимуму, тому що використовують більший обсяг інформації про характер поводження оптимальної функції. У теперішній час для рішення подібних задач розроблено значне число засобів, проте не можна віддати перевагу якому-небудь одному. Вибір засобу визначається складністю об'єкту і задачею оптимізації, що вирішується. Засоби нелiнійного програмування відповідно до засобу визначення кроку пошуку
Всі ці засоби можна назвати прямими ітеративними засобами. Градiєнтні методи рішення задач оптимiзації Градієнт цільової функції
Серед засобів, що застосовуються для рішення задач нелінійного програмування, чимале місце займають засоби пошуку рішення, засновані на аналізі похідної оптимiзуємої функції. Припускаємо надалі, що аналізується тільки диференційовані функції R(U). Розглянемо властивості цих функцій, які можна використовувати для аналізу їх поведінки.
Розглянемо значення функції R(U) у 2-х крапках U та U*, розміщених на ції прямій. Якщо скласти відношення
Рис. 5. 11
та направити довжину відтинку U* - U до нуля, то у межі одержимо величину, становлячи похідною від функції R(U) по напрямку L, тобто
Знайдена похідна характеризує швидкість зміни функції R(U) у точці U за напрямком L. Оскільки через точку U можна провести нескінченну множину прямих по різноманітним напрямкам, отже, у кожній точці для функції R(U) можна визначити незчисленну множину похідних за різними напрямками. Неважко показати, що всі ці похідні можуть бути виражені через похідні за координатами, число яких вже буде кінцевим і рівним розмірності n. За правилом диференціювання складних функцій:
Розрахунок величин dUj/dL розглянемо на слідуючому прикладі. В просторі 2-х перемінних U1 та U2 проведена пряма L (рис. 5.12).
При цьому, з прямокутного трикутника АВС можна записати
Рис.5.12
Аналогічно, для многомірного випадку
Тоді, рівняння (5.32) можна записати
Розглянемо одну з поверхней постійного рівня функції R(
Вирішуючи рівняння (5.37) щодо будь-якої з перемінних, можна збудувати зазначену поверхню, задаючись різноманітними значеннями інших перемінних. Оскільки поверхня постійного рівня (5.37) має n-1 незалежних параметрів, очевидно, її можна представити як поверхня з n-1 вимірами. Так, наприклад, у просторі 2-х перемінних, тобто на площині, ця поверхня вироджується у деяку лінiю, що має тільки один вимір - довжину (рис. 5.13).
Рис.5.13 Рис.5.14 В просторі трьох перемінних поверхня постійного рівня, визначена для функції R(U1, U2, U3), має вже два виміру - довжину та ширину (рис. 5.14). Аналогічно у n-мірному просторі поверхня постійного рівня функції R(
Дотичні та нормаль можуть розглядатися як система координат з початком у обраній точці поверхні. Рис. 5.15 Надана система координат володіє однією важливою властивістю. Часткові похідні від функції R(U) за напрямками осей, що є дотичними до поверхні, дорівнюють нулю, тому що вдовж цих напрямків функція R(U) зберігає постійне значення, оскільки розглядається поверхня постійного рівня функції R(U). Якщо взяти довільний напрямок L, то похідна по ньому, на підставі сказаного, буде мати вигляд:
Це слідує з рівняння (5.36), де похідні по всім осям, за винятком нормалi N, дорівнюють 0. Оскільки cos(α) є функція, що не перевищує по абсолютній величині 1 та приймає максимальне значення при α =0, отже очевидно, що напрямок, за яким похідна dR/dL має максимальне значення, співпадає з напрямком нормалi до поверхні постійного рівня функції R(U). Якщо відкласти на напрямку нормалi вектор з алгебраїчною величиною, рівною похідної dR(U)/dL, то отримаємо вектор, що називається градієнтом скалярної функції R(U) в точці U. Основною властивістю градієнту функції R(U), що позначається як grad R(U) або DR(U), є те, що вектор DR(U) в кожній точці області визначення функції R(U) спрямований за напрямком нормалi до поверхні рівня, проведеної крізь цю точку, та за алгебраїчною величиною дорівнює похідній від зазначеної функції за напрямком нормалi.
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.89.24 (0.01 с.) |
 можна віднести до одного із 3-х типів: безградієнтні засоби; градiєнтні засоби; засоби випадкового пошуку.
можна віднести до одного із 3-х типів: безградієнтні засоби; градiєнтні засоби; засоби випадкового пошуку. В просторі n перемінних Uj, де визначена функція R(U) проводимо лінію у довільному напрямі L
В просторі n перемінних Uj, де визначена функція R(U) проводимо лінію у довільному напрямі L
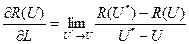 (5.31)
(5.31) (5.32)
(5.32)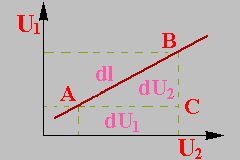 Елемент довжини
Елемент довжини  в даному випадку можна виразити через диференціали перемінних
в даному випадку можна виразити через диференціали перемінних (5.33)
(5.33)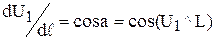 (5.34)
(5.34)

 є ані що інше, як направляючі косинуси обраного напрямку L по відношенню до осей координат
є ані що інше, як направляючі косинуси обраного напрямку L по відношенню до осей координат (5.35)
(5.35) (5.36)
(5.36) ). Ця поверхня характеризується тим, що у будь-якій її точці цільова функція R(
). Ця поверхня характеризується тим, що у будь-якій її точці цільова функція R( (5.37)
(5.37)
 Таким чином, у кожній точці поверхні у n-мірному просторі можна провести n-1 взаємоперпендикулярних дотичних у відповідності з числом вимірів цієї поверхні. Крім отого, в цій точці можна провести вісь, перпендикулярну всім дотичним та, отже, спрямовану по нормалi до поверхні. У вигляді зразку розглянемо випадок, коли число керуючих впливів n=3 (рис. 5.15).
Таким чином, у кожній точці поверхні у n-мірному просторі можна провести n-1 взаємоперпендикулярних дотичних у відповідності з числом вимірів цієї поверхні. Крім отого, в цій точці можна провести вісь, перпендикулярну всім дотичним та, отже, спрямовану по нормалi до поверхні. У вигляді зразку розглянемо випадок, коли число керуючих впливів n=3 (рис. 5.15). (5.38)
(5.38)


