
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однофакторный дисперсионный анализ как проверка статистической гипотезы
Взглянем на дисперсионный анализ с другой стороны. Будем проверять гипотезу о равенстве средних для рассматриваемых групп. В данном случае: Н0: m1 = m2 = m3 (точнее, следовало бы писать: Н0: m·1 = m·2 = m·3) Заметим, что Н1 здесь формулируется достаточно неопределенно – Н1: не все средние равны. Для того, чтобы выяснить, какие именно из средних можно считать неравными, нало использовать специальную технику – методы множественного сравнения. Об этом мы пока не говорим. Вернемся к этому при обсуждении следующей темы. Проверка гипотезы осуществляется знакомым нам образом. Чтобы реализовать соответствующую логику, надо знать критериальную статистику и закон ее распределения. Используем введенные выше обозначения: SSb = SSмежду - межгрупповая сумма квадратов; SSw = SSвнутри – внутригрупповая сумма квадратов; SSt = SSобщ – общая сумма квадратов; n – объем выборки, J – число ячеек. Каждой сумме квадратов отвечает свое число степеней свободы: df b = J-1; df w = Jn – J; df t = Jn – 1. Заметим, что df b + df w = df t.
Введем еще два обозначения: MSb = SSb / df b; MSw = SSw/ df w. Это так называемые средние квадраты. Искомая статистика имеет вид:
Чтобы пояснить тот содержательный смысл, который заложен в этом критерии, вспомним, как выглядит кривая F – распределения. Напомним, что эта кривая имеет два «хвоста» и, соответственно, могут быть найдены два табличных значения:
Как правило, рассматриваемый критерий имеет смысл считать двусторонним (логика рассуждений, использующихся при выборе числа «сторон» критерия – та же, которая была использована нами при обсуждении аналогичного вопроса в случае проверки гипотезы о равенстве двух средних). Для определенности (и в соответствии с традицией), положим, что первое значение ограничивает правый «хвост», а второе – левый. Гипотеза будет отвергнута в двух случаях. Во-первых, если значение критерия достаточно велико. А это будет иметь место, когда числитель дроби MSb / MSw велик, а знаменатель мал. Другими словами, критерий «зашкалит» за правое табличное значение, если наши средние далеко отстоят друг от друга, а внутри каждой группы имеется однородность (т.е. каждое среднее действительно репрезентирует соответствующую группу). Хотелось бы, чтобы читатель понял, что это вполне отвечает здравому смыслу.
Заметим, что аналогичные критерии используются во многих алгоритмах классификации. Мы имеем в виду критерии, позволяющие судить о качестве разбиения. Эти критерии говорят о хорошем качестве, если внутри классов объектам «тесно», а сами классы расположены «просторно», между ними большие расстояния. Таким образом, можно сказать, что дисперсионный анализ не только выводит нас на причинно-следственные отношения, но и позволяет оценить качество классификации, состоящей в распределении объектов по ячейкам. Во-вторых, гипотеза о равенстве средних будет отвергнута, если значение критерия достаточно мало. Смысл этого труднее понять. Однако и здесь обычные житейские рассуждения приходят на помощь. Итак, пусть дробь MSb / MSw очень мала. Грубо говоря, это означает, что либо средние, вычисленные по отдельным классам, очень близки друг к другу, либо разброс значений внутри классов в среднем очень велик. Нетрудно увидеть, что и в том, и в другом случае нет абсолютно никаких оснований отвергать гипотезу, т.е. полагать, что у нас имеются различные средние, хорошо репрезентирующие свои группы. Этого нельзя сказать ни в том случае, если средние «слиплись» (раз они мало отличаются, то вряд ли можно говорить о том, что уровень Y определяется значением X), ни в том, если средние (даже если они разные) не надежны, не отражают ситуацию в группе. Подчеркнем, что мы не доказываем, что средние равны, мы просто полагаем, что выборка не дает нам оснований сомневаться в этом, не дает оснований отвергнуть нуль-гипотезу.
Можно показать, что гипотеза Н0: m1 = m2 =… =m J (14.1) эквивалентна гипотезе Н0: Обычно считаются выполненными условия:
Если же это учесть, то гипотеза (14.1) оказывается эквивалентной гипотезе Н0: и, следовательно, гипотезе Н0:
14.4. О понимании термина «влияет» (или что значит доказать наличие причинно-следственного отношения с помощью дисперсионного анализа)
Итак, приняв гипотезу (14.1), мы полагаем, что фактор Х не влияет на Y. Другими словами, форма обучения не обусловливает (в причинном смысле) уровень усвоения знаний студентами. Отвергнув же названную гипотезу, мы, напротив, полагаем, что уровень знаний студентов причинно обусловлен тем, по какой системе обучаются эти студенты. Хотелось бы, чтобы читатель понимал содержательную значимость подобных выводов. Термины «причинно обусловлен», «влияет» и т.д. здесь употребляются весьма условно. Точно так же мы говорили бы, если бы, скажем, составили частотную таблицу для наших двух признаков (предварительно, конечно, разбив диапазон изменения признака Y на интервалы и начав рассматривать этот признак как номинальный) и рассчитали, к примеру, критерий “Хи-квадрат”. Ответ на вопрос о наличии (отсутствии) связи между признаками мы тоже могли бы интерпретировать как наличие, либо отсутствие соответствующих причинно-следственных отношений. И вывод этот совсем не обязательно совпал бы с выводом, сделанным на основе дисперсионного анализа.
Таким образом, исследователь должен четко понимать, что каждый математический метод дает нам лишь некоторый срез с того явления реальности, который мы назвали причинно-следственным отношением.
14.5. Метод множественных сравнений для однофакторного дисперсионного анализа. Метод множественных сравнений рассмотрим только для однофакторного дисперсионного анализа. Предположим, что, применив однофакторный дисперсионный анализ, мы обнаружили, что проверяемая гипотеза (напомним, что это – гипотеза о равенстве средних всех рассматриваемых ячеек) должна быть отвергнута. Это означает отрицание выражения «средние всех ячеек равны», т.е. утверждение того, что среди средних имеются хотя бы два неравных. Естественно, что подобное утверждение малоинформативно для исследователя. Возникает ряд вопросов: какие именно средние не равны, в каком смысле не равны: может быть, первое – в пять раз больше второго? или же третье равно среднему арифметическому двух первых? и т.д. Найти некоторый (хотя снова не достаточно полный) ответ на эти вопросы и помогает найти метод множественных сравнений. Из двух известных подходов рассмотрим один – т.н. S-метод, связываемый обычно с именем Шеффе[100]. Метод позволяет проверить справедливость некоторой заранее заданной зависимости между генеральными математическими ожиданиями рассматриваемых ячеек. Зависимость эта выражается в определенном виде. Проверка ее справедливости снова происходит на статистическом языке: речь идет о проверке математико-статистической гипотезы о наличии определенного рода связей между изучаемыми средними. Чтобы описать, какого рода связь между средними мы имеем возможность проверить, введем новое определение. Пусть m1 , m 2,,..., m J – рассматриваемые групповые средние, т.е. те самые средние ячеек, гипотезу о равенстве которых мы отвергли в результате применения однофакторного дисперсионного анализа. Опр. Назовем контрастом средних m1 , m 2,,..., m J выражение вида y = с1m1 + с 2 m 2, +... + сJ m J, где с1, с 2 ,... сJ - произвольные действительные числа, удовлетворяющие условию: с1 + с 2 +... + сJ = 0. Смысл введения понятия контраста станет ясным, если мы скажем, что, оказывается, математическая статистика представляет нам средства для проверки гипотез вида: Н0 : y = 0 (для любого контраста y). Чтобы привести примеры контрастов, предположим, что у нас имеется четыре средних m1, m 2, m 3, mJ. Рассмотрим следующие гипотезы и коэффициенты отвечающих им контрастов:
Если будет принята первая гипотеза, это будет означать, что первое и второе средние равны. Значит, неравенство следует искать в отличии третьего или четвертого среднего от первых двух. Принятие второй гипотезы означает, что первое среднее можно считать равным среднему арифметическому значению второго и третьего. Принятие третьей гипотезы заставит нас полагать, что среднее первых двух средних равно среднему последних двух средних.
Примеры задач 1. Для изучения влияния семейного окружения на развитие ребенка были протестированы дети, растущие в разных условиях. Использовался специальный тест, позволяющий оценить уровень развития опрашиваемого (в качестве приписываемых каждому респонденту значений фигурировали целые числа от 0 до 10). Результаты опроса приведены в следующей таблице.
Можно ли сказать, что семейное окружение действительно влияет на развитие ребенка?
2. С помощью однофакторного дисперсионного анализа выявлялось, зависит ли успеваемость студента ГУ-ВШЭ от того, какую школу он окончил. Было изучено три группы студентов-первокурсников, окончивших школу, соответственно, при ГУ-ВШЭ (группа 1), другую среднюю школу в Москве (группа 2), среднюю школу на периферии (группа 3). Успеваемость измерялась с помощью некоторого теста. Гипотеза о равенстве средних была отвергнута. Можно ли каким-нибудь образом проверить гипотезу исследователей о том, что спецшкола при ГУ-ВШЭ дает лучшие знания, чем две другие школы, и что периферийная школа дает более слабые знания, чем каждая из московских. Если можно, то сделать это, воспользовавшись следующими статистическими данными:
Добавочную литературу см. после главы 15.
ТЕМА 15
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.178.133 (0.015 с.) |
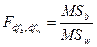 .
.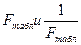 .
.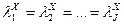 . (14.2)
. (14.2)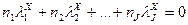 [99] (14.3).
[99] (14.3).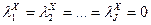
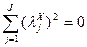 .
.


