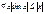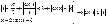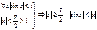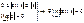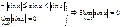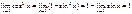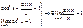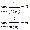Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел ф-ии в точке(Гейне,Коши,правый,левый) Предел ф-ии на бесконечности
Th о пределе ф-ии Первый замечательный предел
Доказательство: докажем для В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке Из рисунка видно, что площадь кругового сектора
2. следовательно, что
1. Покажем, что
2. Докажем, что
3. Последнее утверждение:
Второй замечательный предел lim(n®¥)(1+1/n)^n=e Док-во: x®+¥ n x:n=[x] => n£x<n+1 => 1/(n+1)<1/x<1/n Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n£(1+1/n)^x£ (1+1/n)^(n+1) (4) Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х®+¥, n®¥) lim(n®¥)(1+1/(n+1))=lim(n®¥)(1+1/(n+1))^n+1-1= lim(n®¥)(1+1/(n+1))^n+1*lim(n®¥)1/(1+1/(n+1))=e lim(n®¥)(1+1/n)^n+1= lim(n®¥)(1+1/n)^n* lim(n®¥)(1+1/n)=e*1=e Б-м ф-ии, действия над ними Опр. Ф-ция a(х) наз-ся б/м если ее предел в этой т-ке равен 0 из этого определения вытекает следующее св-во б/м ф-ций: а) Алгебраическая сумма и произведение б/м ф-ций есть б/м ф-ции. б) Произведение б/м ф-ции на ограниченную ф-цию есть б/м ф-ция, т.е. если a(х)®0 при х®х0, а f(x) определена и ограничена ($ С:½j(х)½£С)=> j(х)a(х)®0 при х®х0 Для того чтобы различать б/м по их скорости стремления к 0 вводят сл. понятие: 1) Если отношение 2-х б/м a(х)/b(х)®0 при х®х0 то говорят что б/м a имеет более высокий порядок малости чем b. 2) Если a(х)/b(х)®A¹0 при х®х0 (A-число), то a(х) и b(х) наз-ся б/м одного порядка. 3) если a(х)/b(х)®1, то a(х) и b(х) наз-ся эквивалентными б/м (a(х)~b(х)), при х®х0. 4) Если a(х)/b^n(х)®А¹0, то a(х) наз-ся б/м n-ного порядка относительно b(х). Аналогичные определения для случаев: х®х0-, х®х0+, х®-¥, х®+¥ и х®¥. Б-б ф-ии, связь с б-м Опр. Ф-ия y=f(x) называется бесконечно большой в точке а, если ее предел в этой точке равен бесконечности. (f(x)-б-б)=lim(x->a)(f(x))=∞ Свойства:Пусть y=f(x) и y=g(x) - бесконечно большие ф-ии в точке а. Ф-ия j(х) имеет предел в точке а, отличный от 0 Ф-ия a(х) и b(ч) – бесконечно малые Тогда справедливы следующие утверждения: 1. Произведение двух бесконечно больших ф-ий – бесконечно большая ф-ия.
2. Произведение бесконечно больших на ф-ию, имеющую отличный от нуля предел - бесконечно большая. 3. Ф-ия, обратная величине бесконечно большой – есть бесконечно малая, и наоборот.
Сравнение б-м ф-ии, сравнение б-б ф-ии Определение непрерывности в точке, на отрезке. Опр1.Ф-ия у=f(x) н-ся непрерывной в т.Х0, если lim(x->x0)(f(x))=f(x0) Опр2.Ф-ия f(x) н-ся непрерывной в т Х0, если для любой пос-ти значений аргумента Х: х1,х2,х3….,хn,…. Сходящейся к Х0 соответствующая пос-ть значений ф-ии: f(x1), f(x2),f(x3),....,f(xn),... сходится к числу f(x0), т.е. ("{xn}->x0, xn?X):{f(xn)}->f(x0) Опр3. Ф-ия f(x) н-ся непрерывной в т. Х0, если для любого ε>0 найдется отвечающее ему положительное число δ такое что для всех х, удовлетворяющих условию |x-x0|< δ выполняется нер-во |f(x)-f(x0)|< ε Опр4. Ф-ия f(x) н-ся непрерывной в точке х0, если ее приращение в этой точке является бесконечно малой функцией при ▲x->0, т.е. lim(▲x->0)(▲y)=0 Th о сумме, разн, пр, частн непрер ф-ии Th Пусть ф-ии f(x) и g(x) непрерывны в точке х0. Тогда ф-ии f(x)±g(x), f(x)g(x),f(x)\g(x) также непрерывны в этой точке(для частно g(x0)≠0) Докво.Т.к. ф-ия f(x) непрерывна в точке х0, то lim(x->x0)(g(x))=g(x0). Тогда по теореме о пределах ф-ии пределы ф-ии f(x)+g(x),f(x)g(x) b f(x)\g(x) существуют и соответственно равны f(x0)±g(x0),f(x0)g(x0),f(x0)\g(x0)(g(x0)≠0).Но эти величины равны соответствующим значениям ф-ии в точке х0.Следовательно, согласно определению ф-ии f(x)±g(x),f(x)g(x),f(x)\g(x) непрерывны в точке х0 Точки разрыва ф-ии: (не) устранимый разрыв,1,2 рода Точки, в которых ф-ия не является непрерывной, называются точками разрыва ф-ии. Все т-ки р-рыва делятся на 3 вида: т. устранимого р-рыва; точки р-рыва 1-го, и 2-го рода. а) если в т-ке х0 $ оба односторонних предела, которые совпадают между собой f(x0+)= f(x0-), но ¹ f(x0), то такая т-ка наз-ся точкой устранимого р-рыва. Если х0 т-ка устранимого р-рыва, то можно перераспределить ф-цию f так чтобы она стала непр. в т-ке х0. Если по ф-ции f построить новую ф-цию положив для нее знач. f(x0)= f(x0-)=f(x0+) и сохранить знач. в др. т-ках, то получим исправл. f. б) если в т-ке х0 $ оба 1-стороних предела f(x0±), которые не равны между собой f(x0+)¹f(x0-), то х0 наз-ся т-кой р-рыва первого рода. в) если в т-ке х0 хотя бы 1 из односторонних пределов ф-ции не $ или бесконечен, то х0 наз-ся т-кой р-рыва 2-го рода.
|
|||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.006 с.) |

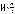 справедливость неравенства
справедливость неравенства 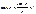
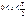

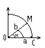
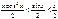 , так как х >0, то
, так как х >0, то 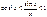 ,
,