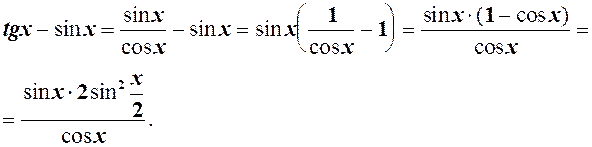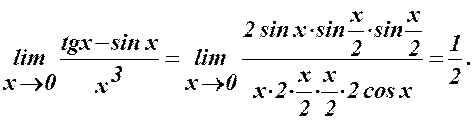Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нескінченно малі величини. Границя змінної.Стр 1 из 4Следующая ⇒
III. Границі Нескінченно малі величини. Границя змінної. Нескінченно великі величини
В цьому розділі при вивчені границь для змінної величини будуть широко використовуватись співвідношення вигляду Отже, значення змінної величини весь час порівнюються із наперед заданими сталими величинами, “поділками шкали”. В математичному аналізі значення малої наперед заданої величини прийнято позначати грецькими буквами Означення 1. Змінна величина х називається нескінченно малою (н.м.) або прямуючою до нуля (позначається
Якщо використати символ
Методична порада. Означення 1 легше запам’ятається, якщо постаратись “озвучити” співвідношення (2). Звертаємо увагу на те, що х в означенні змінна величина. Для кращого розуміння означення 1 рекомендуємо відповісти на такі запитання: 1. Чи можна вважати х н.м., тобто 2. Чи можна вважати 0,00002 нескінченно малою величиною? 3. У циліндричну посудину, на стінках якої по вертикалі нанесено поділки, налита рідина, що витікає через відкритий в дні отвір, х – висота рідини відносно дна при цьому зменшується. Фіксуємо поділку
Означення 2. Змінна х називається прямуючою до числа
Символічний запис:
або ж
Нерівність (4) згідно з співвідношенням (8) (див. 1.3.) можна замінити еквівалентними
Означення 3. Інтервал вигляду (5), що містить точку
Означення 4. Якщо при Наприклад,
Подібно тому, якщо буквою Означення 5. Змінна величина
В символічному записі співвідношення
еквівалентні. Якщо ж При вивченні послідовностей приходиться розглядати окремий випадок нескінченно великої змінної Зустрічаються випадки, коли Якщо кожному натуральному значенню числа Серед послідовностей теж будемо виділяти н.м. Означення 6. Якщо при
Точніше, якщо в означенні 6 перейти до нерівності згідно з означенням 1 нескінченно малої, то отримаємо рівносильне означення. Послідовність
Або якщо ввести ще символ
Приклади. 1. 2. За аналогією з означеннями 5 та 6 можна говорити про нескінченно великі функції Означення 7. Якщо функція
Означення 8. Послідовність
Наприклад: 1. 2.
Нескінченно великими
Нехай
Теорема 1. Сума двох нескінченно малих функцій (послідовностей) є величиною нескінченно малою, тобто
аналогічно для послідовностей
Доведення здійснимо на прикладі послідовностей. Дійсно, із Отже, Аналогічними міркуваннями доводиться теорема для н.м. функцій. Наслідок. Сума скінченного числа нескінченно малих функцій (послідовностей) є величиною н.м.
Зауваження. Вимога скінченної кількості доданків в наслідку є суттєвою. Це видно із наступних прикладів. Нехай 1. 2. 3. Отже, якщо кількість доданків необмежено зростає то, результат додавання н.м. може бути неоднозначним. Такі випадки вивчаються в математичному аналізі в розділі “Ряди”. Означення. Функція
Аналогічно, послідовність нерівність Теорема 2. Добуток нескінченно малої величини на обмежену є нескінченно малою, тобто
і для послідовностей
Доведення на прикладі послідовностей. Для довільного як завгодно малого Теорема 3. Величина обернена до нескінченно великої є нескінченно малою. Навпаки, величина обернена до нескінченно малої є нескінченно великою, напр., для послідовностей
Аналогічні співвідношення між н.м. і н.в. функціями. Приклади. 1. Якщо 2. Якщо
Властивості границь
Теорема 1. Якщо функцію
то
Навпаки, якщо
Дійсно, нехай Навпаки, нехай виконується рівність (2). А це означає, що для
Наслідок. Якщо Дійсно, за теоремою 1 маємо Теорема 2. Нехай існують скінченні границі
Доведемо, наприклад, другу рівність. За теоремою 1(формула 1) з того, що Рівності перша і третя теореми 2 доводяться аналогічно. Наслідок. Сталий множник можна виносити за знак границі, тобто якщо
оскільки Означення 1. Функція Означення 2. Функція Теорема 3. Якщо границя Доведення дамо, коли
Односторонні границі
Будемо розглядати процес, коли змінна Означення. Число Аналогічно, якщо Ліва – і права границі називають односторонніми. Їх ще прийнято позначати
Зауваження. Рівності
еквівалентні Якщо ж односторонні границі різні, тобто
або хоча б одна з них не існує, тоді не існує й границя функції
3.7. Невизначеності. Приклади знаходження деяких границь При знаходженні границі ми використовуємо їх властивості, зокрема теорему 2 із 3.4. Можуть виникати такі випадки. 1. Якщо функція визначена в точці
тобто границя функції збігається з її значенням в точці 2. Якщо ж функція в точці
В більшості таких прикладів для знаходження границі над функціями, що стоять під знаком
1) за наслідками із 2.4 = тобто границя функції збігається з її значенням, бо
.
Зауваження. У загальному випадку, якщо
Це, зокрема, стосується випадку, коли
отримаємо
де Аналогічно для
тоді
4)
5)
3.8. Границя дробово раціональної функції при х ®¥
Розглянемо спочатку наступний приклад 7) = (добуток н.в. на обмежену є н.в.) = ¥. З даного прикладу можна зробити висновок, що у випадку многочлена із степенями різних знаків при
В кожній з дужок обмежені величини. Можливі три випадки: 1) 2)
Перша важлива границя
Першою важливою називається границя
Для доведення (1) будемо виходити із геометричних міркувань (див. рис. 24)
Оскільки
Із
За теоремою 1 із 2.5 про границю нерівностей маємо
що рівносильно (1). На основі (1) отримаємо ще кілька необхідних формул.
Аналогічно
Приклади. 1. 2.
3.
Друга важлива границя Так називається рівність
За формулою (1) розкривається невизначенність вигляду Для доведення (1) перетворимо співвідношення (2) із 3.10.:
Перейшовши формально до границі під знаком логарифма в останній рівності, отримаємо
Замінимо в (2) Зауважимо, що перехід до границі під знаком логарифма ми здійснили формально. Для його строгого обгрунтування потрібно послатись на властивість неперервності цієї функції. Мова про це піде пізніше.
Приклади 1.
2.
3.
Таблиця основних еквівалентних н.м.
1. 2. 3. 4. 5. Формули 1–7 були отримані в попередніх параграфах. Розглянемо останню.
= Наведена таблиця використовувається при розкритті невизначеностей. Нехай н.м. Теорема 1. Границя відношення двох н.м. функцій дорівнює границі відношення їх еквівалентних величин, тобто
Дійсно,
Приклад. 1.
Теорема 2. Якщо
то їх різниця Дійсно,
Теорему 2 треба мати на увазі при знаходженні границь. Розглянемо
Хоча
Тепер
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.95.38 (0.278 с.) |
 ,
,  . Перш ніж дати їх означення, звернемо увагу на те, що одним із засобів вивчення змінної є порівняння її значення із наперед заданими сталими величинами. Наприклад, вивчаючи зміну температури ми спостерігаємо за зміною стовпчика термометра і відносно зафіксованих поділок шкали можемо судити про підвищення або зниження температури, знайти її значення в даний момент. Значення напруги в електромережі вимірюють за допомогою вольтметра. Зміна положення стрілки відносно фіксованих поділок на шкалі прилада дає нам інформацію про зростання або спадання напруги. За рівнем води в річці, яка може спричинити повінь в даному місці, слідкують за допомогою вертикально закріпленої біля берега рейки з нанесеними на ній поділками. Відносно умовного нуля на рейці, так званого нормального рівня, можна встановити на скільки метрів рівень води підвищився або опустився, прослідкувати за нормалізацією рівня, коли його відхилення від нуля прямують до нуля.
. Перш ніж дати їх означення, звернемо увагу на те, що одним із засобів вивчення змінної є порівняння її значення із наперед заданими сталими величинами. Наприклад, вивчаючи зміну температури ми спостерігаємо за зміною стовпчика термометра і відносно зафіксованих поділок шкали можемо судити про підвищення або зниження температури, знайти її значення в даний момент. Значення напруги в електромережі вимірюють за допомогою вольтметра. Зміна положення стрілки відносно фіксованих поділок на шкалі прилада дає нам інформацію про зростання або спадання напруги. За рівнем води в річці, яка може спричинити повінь в даному місці, слідкують за допомогою вертикально закріпленої біля берега рейки з нанесеними на ній поділками. Відносно умовного нуля на рейці, так званого нормального рівня, можна встановити на скільки метрів рівень води підвищився або опустився, прослідкувати за нормалізацією рівня, коли його відхилення від нуля прямують до нуля.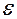 – епсілон, або
– епсілон, або 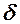 – дельта.
– дельта.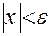 . (1)
. (1)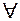 - будь-який довільний, для будь якого довільного, то означення 1 можна записати в символічній формі:
- будь-який довільний, для будь якого довільного, то означення 1 можна записати в символічній формі: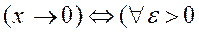
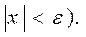 (2)
(2)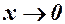 ,якщо умову
,якщо умову  в означені 1 змінити на x <
в означені 1 змінити на x < 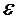 ?
?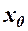 , або число
, або число 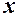 (позначається
(позначається  , або
, або 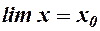 ), якщо їх різниця
), якщо їх різниця 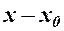 , нескінченно мала, тобто
, нескінченно мала, тобто 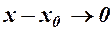 .
.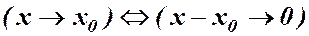 (3)
(3)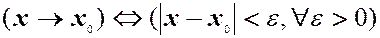 . (4)
. (4)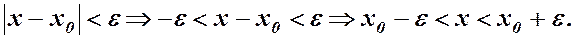 (5)
(5) - окіл з ценром в точці
- окіл з ценром в точці 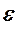 . Рівносильним є співвідношення:
. Рівносильним є співвідношення: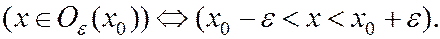 (6)
(6)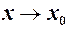 функція
функція 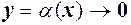 , то
, то  називається нескінченно малою(н.м.) функцією.
називається нескінченно малою(н.м.) функцією. н.м. при
н.м. при  при
при 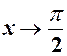 ;
;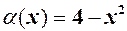 при
при 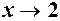 .
.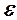 позначаються малі значення для порівняння нескінченно малих, то величини, що зростають, порівнюються із сталими, які позначаються буквою
позначаються малі значення для порівняння нескінченно малих, то величини, що зростають, порівнюються із сталими, які позначаються буквою 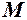 .
.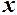 називається нескінченно великою або прямуючою до нескінченності (позначається
називається нескінченно великою або прямуючою до нескінченності (позначається 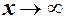 ), якщо в процесі зміни абсолютна величина
), якщо в процесі зміни абсолютна величина 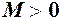 – як завгодно велике наперед задане число, тобто
– як завгодно велике наперед задане число, тобто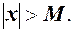
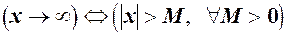 (7)
(7)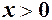 , то пишуть
, то пишуть 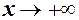 , і якщо
, і якщо 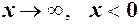 , то пишуть
, то пишуть 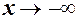 .
.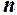 , яка приймає значення натуральних чисел
, яка приймає значення натуральних чисел 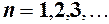 . При цьому значення змінної
. При цьому значення змінної  . Скорочено
. Скорочено 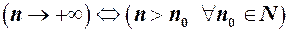 , тобто натуральне число
, тобто натуральне число 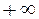 , якщо в процесі зміни воно стане більшим як завгодно великого наперед заданого натурального числа
, якщо в процесі зміни воно стане більшим як завгодно великого наперед заданого натурального числа 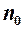 .
.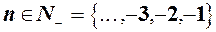 , тоді пишуть
, тоді пишуть 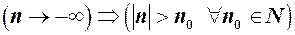 .
.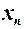 , то маємо послідовність чисел
, то маємо послідовність чисел 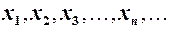 або скорочено
або скорочено 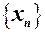 .
.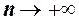 значення деякої послідовності
значення деякої послідовності 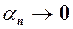 , то така послідовність
, то така послідовність 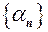 називається нескінченно малою або, ще говорять, збіжною до нуля.
називається нескінченно малою або, ще говорять, збіжною до нуля.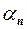 називається н.м. (позначається
називається н.м. (позначається 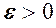 існує номер
існує номер 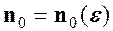 , який залежить від
, який залежить від 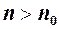 , виконується нерівність
, виконується нерівність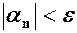 .
.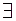 – існує (знайдеться), то в символічному записі маємо:
– існує (знайдеться), то в символічному записі маємо: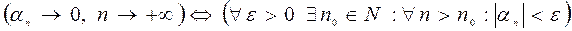
 при
при 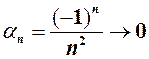 при
при  при
при  при
при 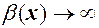 при
при 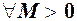 існує число
існує число 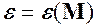 таке, що із нерівності
таке, що із нерівності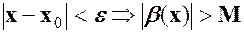 .
. , тобто для
, тобто для 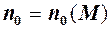 таке, що із нерівності
таке, що із нерівності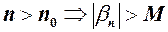 .
.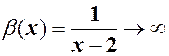 при
при 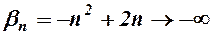 при
при 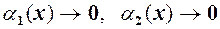 при
при 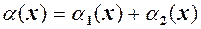 при
при 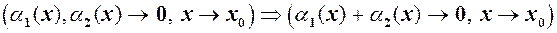 (8)
(8)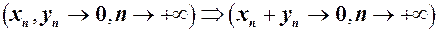 (9)
(9)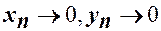 при
при 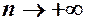 маємо, що для
маємо, що для 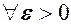 можна знайти номер
можна знайти номер 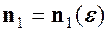 такий, що з нерівності
такий, що з нерівності  . Аналгічно для того ж
. Аналгічно для того ж 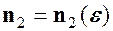 такий, що із нерівності
такий, що із нерівності 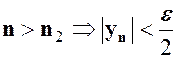 . Тепер для даного
. Тепер для даного  із нерівності
із нерівності 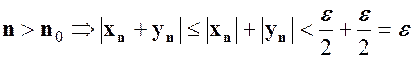 .
.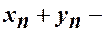 н.м.
н.м.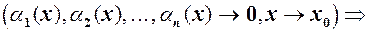
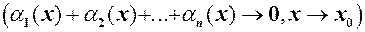 .
.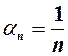 і
і 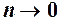 . Розглянемо випадки.
. Розглянемо випадки. стала величина.
стала величина.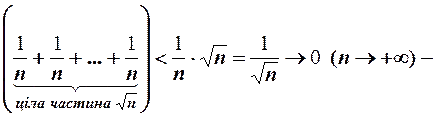 н.м. величина.
н.м. величина.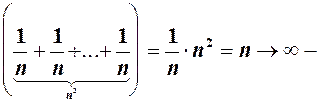 н. велика величина.
н. велика величина. називається обмеженою в області
називається обмеженою в області  , якщо існує число
, якщо існує число  виконується нерівність
виконується нерівність .
.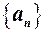 – називається обмеженою, якщо існує число
– називається обмеженою, якщо існує число  виконується
виконується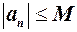 .
.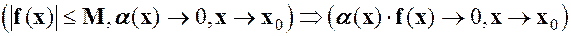 (10)
(10)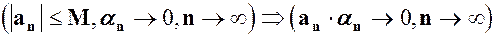 (11)
(11)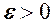 можна вибрати номер
можна вибрати номер 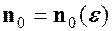 такий, що для натуральних
такий, що для натуральних 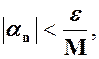 бо
бо 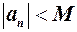 . Отже, тоді
. Отже, тоді 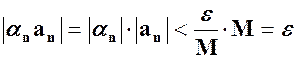 .
.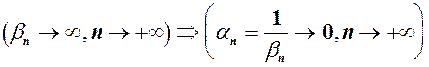 (12)
(12)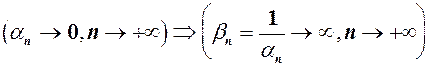 (13)
(13) при
при 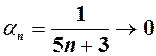 при
при 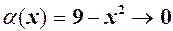 при
при 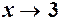 , то
, то 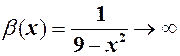 при
при 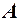 і нескінченно малої
і нескінченно малої 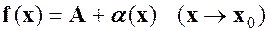 , (1)
, (1)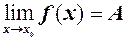 (
(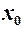 – скінченне або
– скінченне або 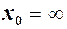 ). (2)
). (2)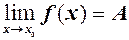 , то можна записати
, то можна записати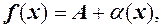 де
де  н.м. при
н.м. при  де
де 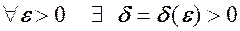 таке, що із нерівності
таке, що із нерівності  нерівність
нерівність 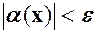 , або
, або 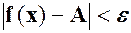 , а це і значить, що має місце рівність (2).
, а це і значить, що має місце рівність (2).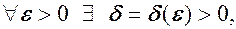 таке, що із
таке, що із 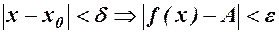 Позначимо
Позначимо 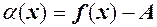 , тоді остання нерівність означає, що
, тоді остання нерівність означає, що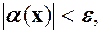 тобто н.м.
тобто н.м.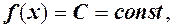 то
то 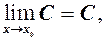 тобто границя сталої величини дорівнює цій сталій.
тобто границя сталої величини дорівнює цій сталій.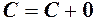 або
або 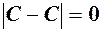 буде меншою
буде меншою 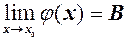 .Тоді
.Тоді 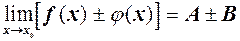 ,
, 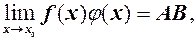
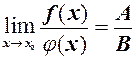 за умови, що
за умови, що 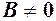 .
.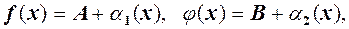 де
де 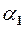 і
і 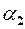 – н.м. при
– н.м. при  н.м. За теоремою 1 маємо, що число
н.м. За теоремою 1 маємо, що число 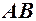 є границею функції
є границею функції 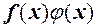 при
при 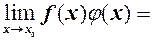

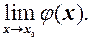
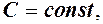 то
то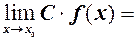

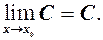
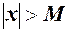 , функція
, функція 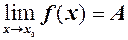 є скінченною, то функція
є скінченною, то функція 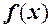 обмежена при
обмежена при 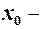 скінченне. Із рівності
скінченне. Із рівності 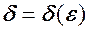 таке, що із
таке, що із 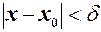 випливає
випливає 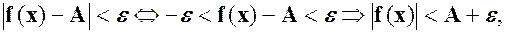 тобто
тобто  , але при цьому
, але при цьому 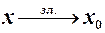 (зл. – зліва), або зручніше записувати
(зл. – зліва), або зручніше записувати 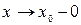 . Аналогічно, якщо
. Аналогічно, якщо 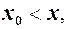 то будемо говорити, що
то будемо говорити, що 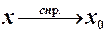 або
або  .
. називається лівою границею функції
називається лівою границею функції 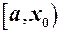 і для неї існує
і для неї існує 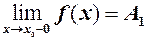 .
.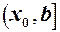 і існує
і існує 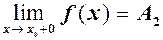 , то
, то 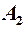 називається правою границею функції
називається правою границею функції 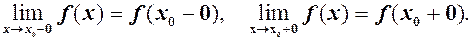
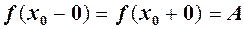
 , тобто якщо односторонні границі існують і рівні в точці
, тобто якщо односторонні границі існують і рівні в точці 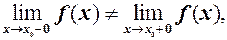
 , то
, то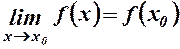 ,
,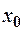 .
.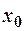 невизначена або
невизначена або  , то можуть зустрітись співвідношення вигляду:
, то можуть зустрітись співвідношення вигляду: 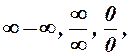
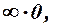
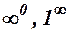 , які називаються невизначеностями.
, які називаються невизначеностями.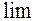 необхідно виконати певні тотожні перетворення, або ще говорять: “позбавитися невизначеності” або “розкрити невизначеність”. А там, де невизначеності не зустрічаються, розв’язання здійснюються у відповідності теореми 2 та властивостей.
необхідно виконати певні тотожні перетворення, або ще говорять: “позбавитися невизначеності” або “розкрити невизначеність”. А там, де невизначеності не зустрічаються, розв’язання здійснюються у відповідності теореми 2 та властивостей. Розглянемо кілька конкретних прикладів з поясненнями
Розглянемо кілька конкретних прикладів з поясненнями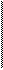 Знайти
Знайти 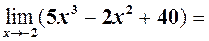 згідно теореми 2, а також =
згідно теореми 2, а також =
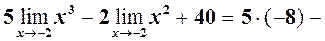
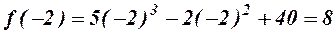 .
.
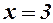 невизначена, і
невизначена, і 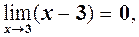 то теорему 2 не можна застосовувати. Робимо перетворення.
то теорему 2 не можна застосовувати. Робимо перетворення.
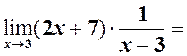
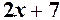 – обмежена
– обмежена
 – н.м., оберненна
– н.м., оберненна
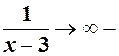 н.в., добуток їх – н.в.
н.в., добуток їх – н.в.
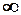

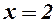 ф. невизначена
ф. невизначена
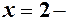 корінь чисельника і знаменника. Розклад на множники
корінь чисельника і знаменника. Розклад на множники
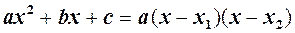
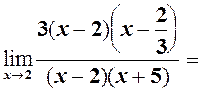
 то на
то на  скорочуємо
скорочуємо
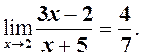
 то необхідно зробити тотожні перетворення так, щоб
то необхідно зробити тотожні перетворення так, щоб 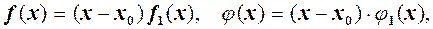 і тоді замість
і тоді замість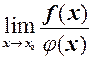 розглянути
розглянути 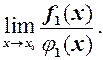
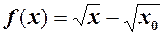 , тоді за допомогою тотожності
, тоді за допомогою тотожності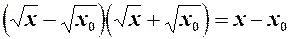 (1)
(1)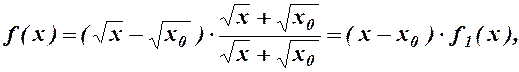
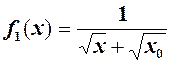 .
. береться тотожність
береться тотожність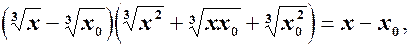 (2)
(2)

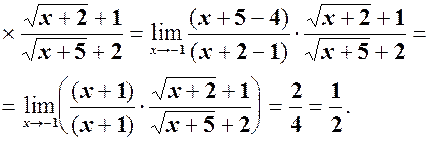
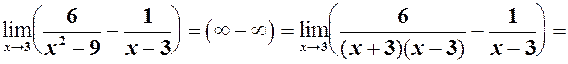
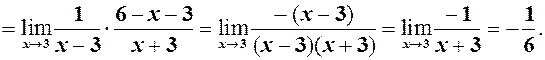

 6)
6) 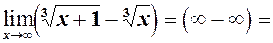 див. формулу (2) =
див. формулу (2) =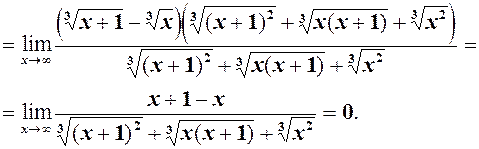

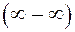 . Щоб її розкрити необхідно винести старший степінь за дужки. Враховуючи цей висновок, розглянемо границю дробово раціональної функції (див. 1.9) при
. Щоб її розкрити необхідно винести старший степінь за дужки. Враховуючи цей висновок, розглянемо границю дробово раціональної функції (див. 1.9) при 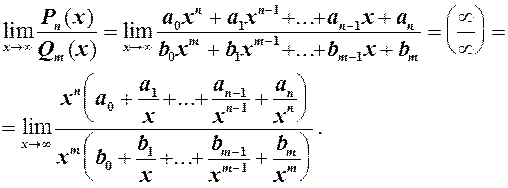
 , тоді степені скорочуються і границя дорівнює відношенню коефіцієнтів при старших степенях
, тоді степені скорочуються і границя дорівнює відношенню коефіцієнтів при старших степенях  ;
;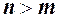 , тоді після скорочення в чисельнику залишиться
, тоді після скорочення в чисельнику залишиться  , тому границя дорівнює ¥;
, тому границя дорівнює ¥;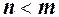 , тоді після скорочення в знаменнику залишиться
, тоді після скорочення в знаменнику залишиться 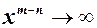 , а обернена до неї
, а обернена до неї  при
при 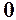 . Отже
. Отже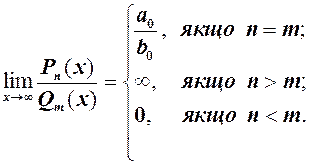 (1)
(1)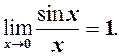 (1)
(1)
 , то вважаємо, що кут 2
, то вважаємо, що кут 2  . Довжина хорди
. Довжина хорди 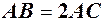 очевидно менша довжини дуги
очевидно менша довжини дуги 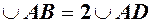 , а дуга
, а дуга 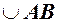 очевидно менша довжини ламаної
очевидно менша довжини ламаної 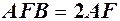 , тобто
, тобто

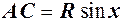 . Довжина дуги
. Довжина дуги 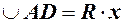 . Із
. Із 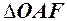 довжина дотичної
довжина дотичної 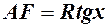 . Отже, нерівність запишеться
. Отже, нерівність запишеться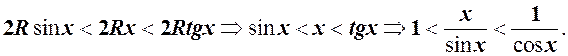
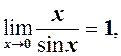
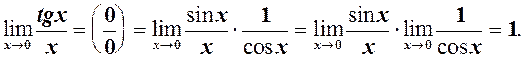
 . (2)
. (2)
 заміна
заміна 
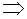

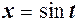 . Якщо
. Якщо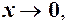 то
то 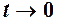
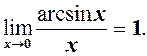 (3)
(3)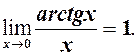 (4)
(4)
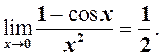 (5)
(5)

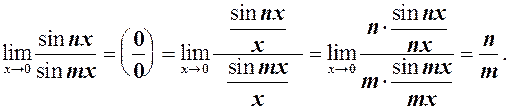
 Заміна
Заміна 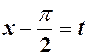 =
=
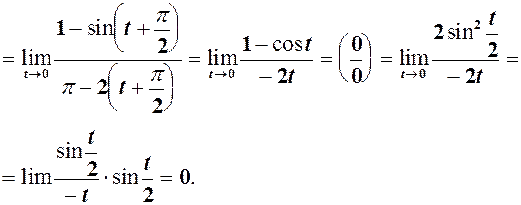

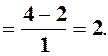
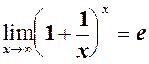 . (1)
. (1)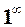 .
.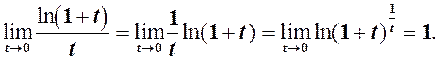
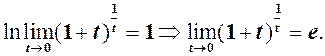
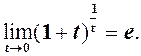 (2)
(2)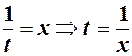 (при
(при 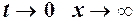 ) одержимо рівносильну рівність (1).
) одержимо рівносильну рівність (1).

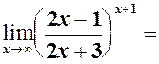 Виділяємо цілу частину =
Виділяємо цілу частину =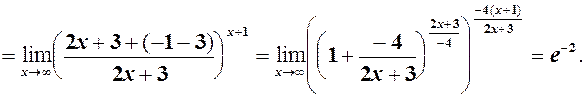

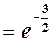 , оскільки
, оскільки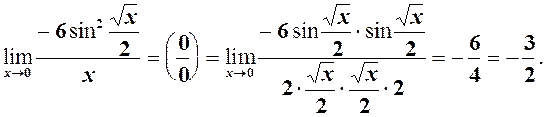
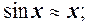 6.
6. 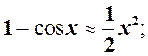
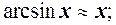 7.
7. 
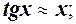 8.
8. 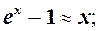
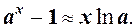
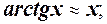
 Заміна
Заміна 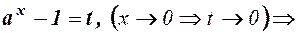 =
=
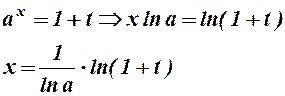
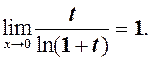
 мають своїми еквівалентними
мають своїми еквівалентними  і
і  , тобто
, тобто 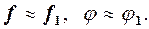 Тоді має місце теорема.
Тоді має місце теорема.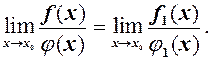
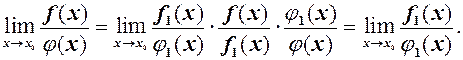
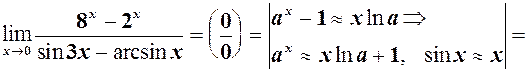

 і
і 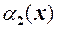 – еквівалентні н.м. (
– еквівалентні н.м. (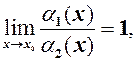
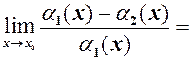
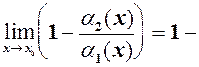
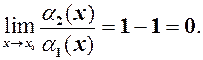
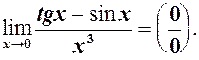
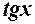 і
і 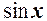 є н.м. першого порядку в порівнянні з
є н.м. першого порядку в порівнянні з 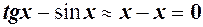 не допоможе. В даному випадку необхідно перетворити
не допоможе. В даному випадку необхідно перетворити