
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 14. Затухающие колебания
свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшиммеханизмом уменьшения энергии колебаний являетсяее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах. Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы (идеализированные реальные системы), в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводитьих моделирование, в том числе и на ЭВМ. Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде
где s – колеблющаяся величина, описывающая тот или иной физический процесс, δ=const – коэффициент затухания, ω0 – циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения (1.127) рассмотрим в виде
где u=u(t). После нахождения первой и второй производных выражения (1.128) и подстановкиих в (1.127) получим
Решение уравнения (1.129) зависит от знака коэффициента перед искомой величиной. рассмотрим случай, когда этот коэффициент положителен:
(если (ω02 – δ2)>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа (1.100) ű + ω2u = 0, решением которого является функция u=A0cos(ωt+φ)(см.(1.81)). Таким образом, решение уравнения (1.127) в случае малых затуханий (δ2<<ω2)
- амплитуда затухающих колебаний, а А0 – начальная амплитуда. Зависимость (1.131) показана на рисунке 1.60 сплошной линией, а зависимость (1.132) – штриховыми линиями. Промежуток времени τ = 1/δ, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющееся физической величины (рисунок 1.60). Тогда период затухающих колебаний с учетом формулы (1.130) равен
Рисунок 1.60 Если А (t) и A(t+Т) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
называется декрементом затухания, а его логарифм
логарифмическим декрементом затухания; Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания - постоянная для данной колебательной системы величина. Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна
(так как затухание мало (δ2<<ω2), то T принято равным То). Из формулы (1.136) следует, что добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации. Выводы, полученные для свободных затухающих колебаний линейных систем, применимы для колебаний различной физической природы – механических (в качестве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический колебательный контур). 1. Свободные затухающее колебания пружинного маятника. Для пружинного маятника массой т, совершающего малые колебания под действием упругой силы F= – kx, сила трения пропорциональна скорости, т. е.
где r – коэффициент сопротивлеиия; знак минус указывает на противоположные направления силы трения и скорости. При данных условиях закон движения маятника будет иметь вид
Используя формулу
получим идентичное уравнению (1.127) дифференциальное уравнение затухающих колебаний маятника:
Из выражений (1.127) и (1.131) вытекает, что колебания маятника подчиняются закону
где частота Добротность пружинного маятника, согласно (1.136) и (1.139), В заключение отметим, что при увеличении коэффициента затухания δ период затухающих колебаний растет и при δ=ω0 обращается в бесконечность, т. е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t→∞. Процесс не будет колебательным. Он называется апериодическим. Наибольший интерес длятехники представляют незатухающие колебания. Для этого необходимо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы так называемые автоколебаиия – незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой. Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний, происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями). Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй. Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 853; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.006 с.) |
 .
.

 ,
,

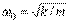 (см. (1.103)) и принимая, что коэффициент затухания
(см. (1.103)) и принимая, что коэффициент затухания
 (см. (1.130)).
(см. (1.130)).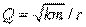 .
.


