
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Числовые характеристики случайных величин
Математическое ожидание дискретных и непрерывных случайных величин. Вероятностный смысл математического ожидания. Постоянная величина, произведение постоянной на случайную, сумма случайных величин. Отклонение случайной величины от ее центра. Независимые и взаимно независимые случайные величины. Произведение случайных величин. Квадрат случайной величины, целая положительная степень случайной величины. Свойства математического ожидания. Мода и медиана. Дисперсия дискретных и непрерывных случайных величин. Свойства дисперсии. Формула для вычисления дисперсии. Среднее квадратичное отклонение. Понятие о моментах распределения. Коэффициент корреляции и его свойства.
Л и т е р а т у р а
[2], гл.4, § 1, 3, 5, 6; [3], гл.5, 5.5-5.7, гл.10, 10.2; [5], гл.7, § 1-4, гл.8, § 1-5, 7-10, гл.12, § 1; [6], гл.5; [7], гл.8, § 20, гл.9, § 21, 22, гл.10, § 23-25; [8], гл.3, § 2-4, гл.4, § 4, 6; [9], гл.2, § 7-9, гл.3, § 8; [10], гл.4, § 1, 2; [11], гл.29, § 201, 202, 204; [12], гл.3, § 10, 11; [13], гл.20, § 9, 10, 14; [14], § 2; [15], гл.6, § 1-4; [16], гл.2, 2.2.4.
О с н о в н ы е п о л о ж е н и я и ф о р м у л ы
Математическое ожидание М(Х) дискретной случайной величины с конечным числом значений определяется равенством М(Х) = и в случае счетного числа значений – равенством М(Х) = при этом предполагается, что ряд абсолютно сходится. Для непрерывной случайной величины М(Х) определяется формулой М(Х) = Интегралы в равенстве (5.3) берутся по соответствующему множеству значений случайной величины, при этом предполагается, что несобственные интегралы сходятся абсолютно. Пусть С – постоянная величина. Тогда М(С)=С, М(СХ)=СМ(Х). (5.4) Математическое ожидание алгебраической суммы двух случайных величин равно сумме математических ожиданий слагаемых: М(Х±Y) = М(Х) ±М(Y). (5.5) Это свойство распространяется на любое конечное число слагаемых. Если Х и Y независимы, то М(ХY) = М(Х) М(Y). (5.6) Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий. Случайная величина Х-М(Х) называется отклонением случайной величины от ее центра. Математическое ожидание отклонения равно нулю: М[X-М(Х)] = 0. (5.7) Дисперсией (рассеянием) Д(Х) случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее центра (математического ожидания):
Д(Х) = М[Х-М(Х)]2. (5.8) Для вычисления дисперсии используется формула Д(Х) = М(Х2) – [М(Х)]2. (5.9) Дисперсия обладает свойствами Д(С) = 0, Д(СХ)=С2Д(Х). (5.10) Если Х и Y независимы, то Д(Х±Y) = Д(Х) + Д(Y). (5.11) Среднее квадратическое отклонение s(Х) случайной величины Х определяется равенством s(X) = Число n k = М [(X-C)k], (5.13) называется моментом k-го порядка случайной величины Х. Если С =0, то момент называется начальным. Само математическое ожидание есть начальный момент первого порядка. Если С = М(Х), то момент называется центральным. Легко видеть, что центральный момент второго порядка есть не что иное, как дисперсия. Коэффициентом корреляции r(Х, Y) между случайными величинами Х и Y называется число r(Х, Y) = Если Х и Y нормировать, т.е. ввести величины Х 1= Часто приходится находить закон распределения случайной величины Y =y(Х) при известном законе распределения Х. Для дискретной случайной величины Х, принимающей значения х i с вероятностями рi, полагают, что Y =y(Х) принимает значения yi=y(x i) с теми же вероятностями рi. При этом, если некоторым х i будут соответствовать равные между собой значения yi, то в ряде распределения случайной величины Y эти yi записываются только один раз с вероятностью, равной сумме соответствующих вероятностей. Пусть Х и Y – дискретные случайные величины, при этом Х принимает значения х i с вероятностями Р (Х =хi), а Y – значения yj с вероятностями Р (Y =yj). Тогда их сумма Х+Y, разность Х-Y, произведение XY соответственно принимают всевозможные значения х i + yj, х i – yj , х i yj с вероятностями рij, определяемыми формулой рij = Р (Х = х i) ´ а для независимых случайных величин – формулой рij = Р (Х = х i) ´ Р (Y =yj). (5.16) При этом, если при некоторых i и j величины х i + yj, х i – yj , х i yj примут равные значения, то соответствующая вероятность есть сумма вероятностей по этим индексам i, j.
|
|||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 754; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.87.95 (0.006 с.) |
 (5.1)
(5.1) (5.2)
(5.2)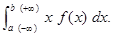 (5.3)
(5.3) . (5.12)
. (5.12) nk, определяемое равенством
nk, определяемое равенством . (5.14)
. (5.14) , Y 1=
, Y 1= 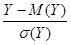 , то r(Х, Y)= М (Х 1 Y 1). Если Х и Y независимы, то очевидно, что r(Х, Y)=0. Можно доказать, что
, то r(Х, Y)= М (Х 1 Y 1). Если Х и Y независимы, то очевидно, что r(Х, Y)=0. Можно доказать, что 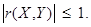
 (Y=yj), (5.15)
(Y=yj), (5.15)


