
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экспоненциальный закон распределения вероятностей. Функция надежности ⇐ ПредыдущаяСтр 2 из 2
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
функция распределения вероятностей имеет вид:
График:
Вероятность попадания случайной величины в интервал (а;в) находится по формуле: P (a<X<b) = Для показательного распределения: M(X)= 1/λ D(X)= 1/ σ(X) = 1/λ Ф-ция надежности Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению R(T) = P(T>t) – вероятность безотказной работы некоторого устройства за время t: Показательный закон надежности – R(T)= 23. Двумерные случайные величины. Условные законы распределения составляющих системы дискретных и непрерывных случайных величин Пусть(Х,У)- двумерная случайная величина, тогда ее распределение можно представить в виде табл. распределения, в каждой клетке (i,j), которой располагается вероятность произведения событий
Условным законом распределения одной из составляющих двумерной дискретной случ. величины (X,Y) называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенные значения. Пусть дана двумерная дискретная случ.величина (X,Y) X1,x2 …xn;y1,y2…yn Будем обознач.условные вероятности составляющей X P(xi/yi) (i= 1,2…n;j= 1,2…n) Условным распределением составляющей Xпри Y=yiназывают совокупность условных вероятностей p(x1/yj), p(x2/yj),…p(xi/yj), вычисленных в предположении, что событиеY=yi уже наступило Зная закон распределения двумерной дискретной случайной величины, можно вычислить условные законы составляющей Условные законы распределения составляющей X определяется соотношением: P(xi/yj)= P(xi/yj)/P(yj) P(yj/xi)= P (xi/yj)/ P(xi)
В случае дискретной двумерной случайной величины ее функция распределения F(X,Y) = Числовые характеристики системы двух случайных величин
Условным математич. ожиданием дискретной случайной величины У при Х=х называают сумму произведений возможных значений Yна их условные вероятности: М(У/X=x)= Для непрерывной величины: М(У/X=x) = Зависимые и независимые случайные величины. Ковариация и коэффициент корреляции Теорема. Для того, чтобы случ. Величины Х и У были независимыми необходимо и достаточно, чтобы функция распределения системы (Х,У) была = произведению фун-ций распределения составляющих: F(x,y)=F1(x)F2(y) Ковариацией (или корреляционным моментом) наз-ся мат. Ожидание произведения отклонения этих величин от своих мат. Ожиданий: Мху=М[(X-M(X))*(Y-M(Y))] Mxy=M(XY)-M(X)*M(Y) Для вычисления корреляционного момента(ковариации) дискретных случ. Величин используют формулу: Mxy= Для непрерывных Mxy= Корреляционный момент служит для хар-ки связи и между величинами Х и У. Теорема 1. Корреляционный момент двух независимых случ. Величин Х и У=0. Коэффициентом корреляции двух случ. Величин наз-ся отношение их ковариации к произведению средних квадратичных отклонений эти величин: rxy=Mxy/σxσy Теорема 2. Абсолютная величина корреляционного момента двух случ. Величин Х и У не превышает среднего геометрического их дисперсий. Уравнение линейной регрессии У на Х и Х на У. Коэффициент регрессии Линейной средней квадратичной регрессией У и Х называется функция вида:
Коэффициент β=
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.141.202 (0.006 с.) |



 -
- 

 ,λ-интенсивность отказов. Функция R(T)называется функцией надежности
,λ-интенсивность отказов. Функция R(T)называется функцией надежности = P(X=xi,Y=yj)
= P(X=xi,Y=yj)
 , где суммирование вероятностей распространяется на все i,для которых xi<x и все j, для которых yj<y
, где суммирование вероятностей распространяется на все i,для которых xi<x и все j, для которых yj<y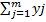 * p (yj/x)
* p (yj/x) *ψ(Y/X)dy
*ψ(Y/X)dy [x1-M(X)][y1-M(Y)]p(x1,y1)
[x1-M(X)][y1-M(Y)]p(x1,y1) =
= 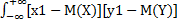 f(x,y)dxdy
f(x,y)dxdy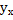 =
=  +
+  (x-
(x-  ), где
), где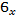 =
=  ,
,  =
= 
 =
=  (y-
(y-  (1-
(1-  ) – остаточная дисперсия. Характеризует величину ошибки, которую допускают при замене Х линейной функции от У
) – остаточная дисперсия. Характеризует величину ошибки, которую допускают при замене Х линейной функции от У


