
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип максимума Понтрягина
Принцип максимума является специальным методом решения задач оптимального управления. Этот метод разработан в 1956–1961 годах Л.С.Понтрягиным и его сотрудниками. Главным достоинством принципа максимума является то, что класс искомых экстремалей включает в себя кусочно непрерывные функции. В этом смысле принцип максимума является расширением классического вариационного исчисления. Во многих прикладных задачах на управление накладывается ограничение типа неравенства. Часто оптимальное управление в таких задачах имеет разрыв. Метод множителей Лагранжа не позволяет определить число и местоположение точек разрыва, и поэтому в этих случаях он не позволяет находить оптимальное управление. Такие задачи эффективно решаются с помощью принципа максимума Понтрягина. Задача с закрепленными концами И фиксированным временем Все теоремы принципа максимума относятся к системам, поведение которых можно описать дифференциальными уравнениями:
где Ставится задача – найти управление
Замечаем, что в отличие от обычных задач вариационного исчисления, где все искомые функции были равноправны, в принципе максимума разделяются фазовые координаты и управления. Это разделение удобно в тех случаях, когда ограничения накладываются только на управления, а не на фазовые координаты, например, если задано
Важную роль в принципе максимума играют вспомогательные переменные
При помощи этой функции основная система уравнений (4.1) и уравнения, необходимые для определения вспомогательных переменных
Действительно, так как
Теорема 4.1. Для оптимальности управления
Кроме того, в конечный момент времени
Доказательство этой теоремы основано на использовании игольчатой вариации [2, с.208–240]. При решении задач с помощью принципа максимума удобно придерживаться следующего алгоритма: 1. Записываем уравнения объекта в виде системы уравнений первого порядка (4.1), не забыв уравнение для функционала (4.2):
2. Составляем функцию
3. Определяем значение
Возможно, что максимум В уравнениях (4.8) для определения 4. Составляем уравнения (4.5) для определения
Из совместного решения названных Особенностью принципа максимума является то, что вариационная задача нахождения функции Отметим, что, используя теорему о максимуме, мы отыскиваем решение не в классе кусочно-гладких функций, а в более широком классе – классе кусочно-непрерывных функций.
|
|||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 2100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.178 (0.006 с.) |
 , (4.1)
, (4.1) – вектор фазового пространства и
– вектор фазового пространства и  – вектор управления, причем производные от управлений в уравнения (4.1) не входят.
– вектор управления, причем производные от управлений в уравнения (4.1) не входят. в состояние
в состояние  за время
за время  и доставляющее минимум функционалу
и доставляющее минимум функционалу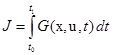 . (4.2)
. (4.2) .
. и промежуточная функция, которая называется функцией Гамильтона (или гамильтонианом):
и промежуточная функция, которая называется функцией Гамильтона (или гамильтонианом): . (4.3)
. (4.3) (4.4)
(4.4) (4.5)
(4.5) , то уравнения (4.4) эквивалентны уравнениям (4.1); в то же время из уравнений (4.5) можно найти вспомогательные переменные
, то уравнения (4.4) эквивалентны уравнениям (4.1); в то же время из уравнений (4.5) можно найти вспомогательные переменные  для того, чтобы быть оптимальным, формулируется в виде теоремы о максимуме:
для того, чтобы быть оптимальным, формулируется в виде теоремы о максимуме: и траектории
и траектории  необходимо существование такой ненулевой непрерывной функции
необходимо существование такой ненулевой непрерывной функции  , удовлетворяющей уравнениям (4.5), что при любом
, удовлетворяющей уравнениям (4.5), что при любом  , кроме точек разрыва
, кроме точек разрыва  достигает максимума, т.е.
достигает максимума, т.е. . (4.6)
. (4.6) выполняются соотношения:
выполняются соотношения: . (4.7)
. (4.7) .
.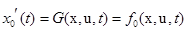 .
. :
: , максимизирующее функцию
, максимизирующее функцию  . (4.8)
. (4.8)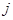 равенство (4.8) может не выполняться при ненулевой функции
равенство (4.8) может не выполняться при ненулевой функции  неизвестных:
неизвестных:  функций
функций  ,
,  функций
функций 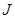 , заменена более простой задачей математического анализа нахождения параметра
, заменена более простой задачей математического анализа нахождения параметра  , доставляющего максимум вспомогательной функции
, доставляющего максимум вспомогательной функции  . Отсюда и название метода – принцип максимума.
. Отсюда и название метода – принцип максимума.


