
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування визначеного інтеграла до геометрії
1. Обчислити площу фігури, обмеженої параболою 2. Обчислити об’єм тіла, яке утворюється обертанням навколо осі 0y фігури, обмеженої параболами 3. Обчислити об’єм тіла, яке утворюється обертанням навколо осі 0y фігури, обмеженої параболами 4. Обчислити площу фігури, обмеженої лініями 5. Обчислити площу фігури, обмеженої лініями 6. Обчислити площу фігури, обмеженої параболою 7. Обчислити об’єм тіла, утвореного обертанням навколо осі абсцис фігури, яка обмежена лініями 8. Обчислити площу фігури, обмеженої параболою 9. Обчислити об’єм тіла, утвореного обертанням навколо осі ординат фігури, яка обмежена параболами 10. Обчислити площу фігури, обмеженої параболою 11. Обчислити об’єм тіла, утвореного обертанням навколо осі абсцис фігури, яка обмежена гіперболою 12. Обчислити об’єм тіла, утвореного обертанням навколо осі 0x плоскої фігури, яка обмежена віссю абсцис і параболою 13. Обчислити об’єм тіла, утвореного обертанням навколо осі 0x фігури, яка обмежена параболою 14. Обчислити об’єм тіла, утвореного обертанням навколо осі 0y фігури, яка обмежена гіперболою 15. Обчислити площу фігури, обмеженої параболою 16. Обчислити площу фігури, обмеженої параболою 17. Обчислити площу фігури, обмеженої параболою 18. Обчислити площу фігури, обмеженої параболою 19. Обчислити площу фігури, обмеженої лініями 20. Обчислити площу фігури, обмеженої лініями 21. Обчислити площу фігури, обмеженої лініями 22. Обчислити площу фігури, обмеженої прямою 23. Обчислити площу фігури, обмеженої параболою 24. Обчислити площу фігури, обмеженої параболою 25. Обчислити площу фігури, обмеженої параболою 26. Обчислити площу фігури, обмеженої лініями 27. Обчислити площу фігури, обмеженої параболою 28. Обчислити площу фігури, обмеженої параболою 29. Обчислити площу фігури, обмеженої параболою 30. Обчислити площу фігури, обмеженої параболою 31. Обчислити об’єм тіла, утвореного обертанням навколо осі абсцис фігури, яка обмежена лініями
32. Обчислити об’єм тіла, утвореного обертанням навколо осі абсцис фігури, яка обмежена параболами 5. Знайти частинні похідні функції z=f(x,y).
1)
3)
5)
7)
9)
11)
13)
15)
17)
19)
21)
23)
25)
27)
29)
31)
6. Задано функцію z=f(x,y) і дві точки: A (x0; y0) і B (x 1; y 1). Обчислити: а) значення функції в точці В; б) наближене значення функції в точці В, виходячи зі значення її в точці А і замінивши приріст функції при переході від точки А до точки В диференціалом; в) відносну похибку, обумовлену заміною приросту функції диференціалом.
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32)
7. Знайти: а) градієнт функції z=f(x,y) у точці А; б) похідну функції z=f(x,y) у точці А за напрямком вектора 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32)
8. Знайти загальний розв`язок диференціального рівняння.
1) 3) 5) 7) 9) 11) 13) 15) 17) 19) 21) 23) 25) 27) 29) 31)
9. Знайти загальний розв`язок диференціального рівняння.
1) 3) 5) 7) 9) 11) 13) 15) 17) 19) 21) 23) 25) 27) 29) 31)
10. Знайти частинний розв`язок диференціального рівняння, який задовольняє вказані початкові умови.
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32)
11. Розв`язати систему лінійних диференціальних рівнянь.
1) 3) 5) 7) 9) 11) 13) 15) 17)
19)
21)
23)
25)
27) 29) 31)
Розв’язування типових прикладів Завдання 1. 1. Знайти інтеграл
Перевіримо диференціюванням вірність отриманого розв’язку. Для цього знайдемо похідну
Отримали підінтегральну функцію. 2. Знайти інтеграл
3. Знайти інтеграл Використаємо формулу інтегрування частинами
Нехай
Перевіримо диференціюванням вірність отриманого розв’язку. Для цього знайдемо похідну
= Отримали підінтегральну функцію. 4. Знайти інтеграл Перетворимо знаменник дробу, що стоїть під знаком інтеграла наступним чином:
Тоді після підстановки
При обчисленні інтеграла
5. Обчислити інтеграл Підінтегральна функція – неправильний дріб, тому, розділивши чисельник на знаменник, виділимо цілу частину
Правильний дріб розкладемо на суму елементарних дробів
де А, В, С, D – невизначені коефіцієнти. Звідси
Надамо х чотири різних значення (по кількості невизначених коефіцієнтів):
Розв’язавши систему лінійних рівнянь отримаємо Тоді
Остаточно маємо
6. Обчислити інтеграл Виконаємо підстановку
7. Знайти інтеграл Скористаємося універсальною тригонометричною підстановкою
Завдання 2. 1. Нехай необхідно обчислити інтеграл Використаємо формулу Ньютона–Лейбніца
Щоб обчислити визначений інтеграл
2. Обчислити інтеграл При обчисленні даного інтегралу зробимо заміну змінної. В цьому випадку знаходимо нові границі інтегрування для нової змінної.
Завдання 3. Обчислити інтеграл.
Завдання 4. 1. Обчислити площу фігури, обмеженої заданими параболами
Розв’язування. Знайдемо абсциси точок перетину заданих парабол. Для цього прирівняємо праві частини цих рівнянь:
Звідси
де В нашому випадку маємо
2. Знайти об’єм тіла, утвореного обертанням навколо осі Ох фігури, розташованої в першій координатній чверті і обмеженої параболою
Розв’язування. Знайдемо абсцису точки перетину параболи і прямої в першій координатній чверті. Для цього розв’яжемо рівняння
Абсцису точки перетину прямої з віссю Ох знайдемо, розв’язавши рівняння Таким чином, можемо вважати, що тіло обертання обмежене при
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.59.231 (0.228 с.) |
 і прямою
і прямою  .
. .
. .
. ,
,  і прямою
і прямою  .
. ,
,  і віссю абсцис.
і віссю абсцис. і прямою
і прямою  .
. і
і  і прямою
і прямою  .
. і
і  .
. і віссю абсцис.
і віссю абсцис. , прямими
, прямими  ,
,  і віссю абсцис.
і віссю абсцис. .
. , прямою
, прямою 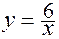 , віссю 0y і прямими
, віссю 0y і прямими  і
і  .
. і прямою
і прямою  .
. і прямою
і прямою  .
.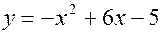 і прямою
і прямою  .
. .
. і
і  .
. і
і  .
. і
і  .
. і параболою
і параболою  .
. і прямою
і прямою  .
.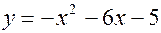 і прямою
і прямою  і прямою
і прямою  і
і  .
. і прямою
і прямою  і прямою
і прямою  .
. і прямою
і прямою  .
. і прямою
і прямою  .
. і
і  .
. і
і  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  ;
; ; 18)
; 18)  ;
; ; 20)
; 20)  ;
; ; 22)
; 22)  ;
; ; 24)
; 24)  ;
;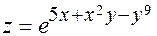 ; 26)
; 26)  ;
; ; 28)
; 28)  ;
; ; 30)
; 30)  ;
; ; 32)
; 32)  .
. ; A(1; 2); B(1,02; 1,96);
; A(1; 2); B(1,02; 1,96); ; A(1; 3); B(1,06; 2,92);
; A(1; 3); B(1,06; 2,92); ; A(4; 1); B(3,96; 1,03);
; A(4; 1); B(3,96; 1,03); ; A(2; 3); B(2,02; 2,97);
; A(2; 3); B(2,02; 2,97);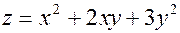 ; A(2; 1); B(1,96; 1,04);
; A(2; 1); B(1,96; 1,04); ; A(2; 4); B(1,98; 3,91);
; A(2; 4); B(1,98; 3,91); ; A(-1; 3); B(-0,98; 2,97);
; A(-1; 3); B(-0,98; 2,97); ; A(3; 2); B(3,05; 1,98);
; A(3; 2); B(3,05; 1,98); ; A(3; 4); B(3,04; 3,95);
; A(3; 4); B(3,04; 3,95); ; A(1; 2); B(0,97; 2,03);
; A(1; 2); B(0,97; 2,03); ; A(2; 1); B(1,98; 1,03);
; A(2; 1); B(1,98; 1,03); ; A(1; 2); B(1,02; 1,91);
; A(1; 2); B(1,02; 1,91); ; A(-1; 1); B(-0,98; 0,97);
; A(-1; 1); B(-0,98; 0,97); ; A(1; -1); B(1,02; -0,97);
; A(1; -1); B(1,02; -0,97); ; A(1; 1); B(1,03; 0,98);
; A(1; 1); B(1,03; 0,98); ; A(2; -1); B(1,98; -0,97);
; A(2; -1); B(1,98; -0,97); ; A(-2; 1); B(-1,97; 0,98);
; A(-2; 1); B(-1,97; 0,98); ; A(-1; 2); B(-0,98; 1,97);
; A(-1; 2); B(-0,98; 1,97); ; A(2; -1); B(1,97; -1,02);
; A(2; -1); B(1,97; -1,02); ; A(1; -2); B(1,03; -2,02);
; A(1; -2); B(1,03; -2,02); ; A(2; 1); B(2,03; 0,96);
; A(2; 1); B(2,03; 0,96); ; A(-2; 2); B(-2,02; 2,05);
; A(-2; 2); B(-2,02; 2,05); ; A(1; 3); B(0,95; 2,94);
; A(1; 3); B(0,95; 2,94); ; A(1; 3); B(0,96; 2,95);
; A(1; 3); B(0,96; 2,95); ; A(2; 2); B(1,93; 2,05);
; A(2; 2); B(1,93; 2,05); ; A(1; 3); B(1,07; 2,94);
; A(1; 3); B(1,07; 2,94); ; A(1,5; 2,3); B(1,43; 2,35);
; A(1,5; 2,3); B(1,43; 2,35); ; A(-4; 5); B(-3,92; 5,06);
; A(-4; 5); B(-3,92; 5,06);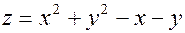 ; A(1; -3); B(1,08; -2,94);
; A(1; -3); B(1,08; -2,94); ; A(1; 2); B(1,03; 1,97);
; A(1; 2); B(1,03; 1,97); ; A(-1; 2); B(-0,97; 2,01);
; A(-1; 2); B(-0,97; 2,01); ; A(1; 3); B(0,98; 2,95).
; A(1; 3); B(0,98; 2,95). .
. ; A(2; 1);
; A(2; 1);  ; A(1; 1);
; A(1; 1);  ; A(1; 1);
; A(1; 1);  ; A(2; 1);
; A(2; 1);  ; A(2; 3);
; A(2; 3);  ; A(1; 2);
; A(1; 2);  ; A(1; 3);
; A(1; 3);  ; A(-1; 2);
; A(-1; 2);  ; A(1; 1);
; A(1; 1);  ; A(-1; 2);
; A(-1; 2);  ; A(-1; 1);
; A(-1; 1); 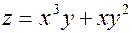 ; A(1; 3);
; A(1; 3);  ; A(2; 2);
; A(2; 2);  ; A(1; 1);
; A(1; 1);  ; A(3; 4);
; A(3; 4);  ; A(2; 3);
; A(2; 3);  ; A(1; 2);
; A(1; 2);  ; A(1; -2);
; A(1; -2);  ; A(1; 1);
; A(1; 1);  ; A(-1; 2);
; A(-1; 2);  ; A(2; -2);
; A(2; -2);  ; A(1; 3);
; A(1; 3);  ; A(3; -2);
; A(3; -2);  ; A(1; 4);
; A(1; 4);  ; A(1; -1);
; A(1; -1);  ; A(-2; 4);
; A(-2; 4);  ; A(4; 3);
; A(4; 3);  ; A(2; 1);
; A(2; 1);  ; A(-2; 2);
; A(-2; 2); 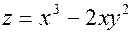 ; A(1; 2);
; A(1; 2);  ; A(-2; 1);
; A(-2; 1);  ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  ;
; ; 18)
; 18)  ;
; ; 20)
; 20)  ;
; ; 22)
; 22)  ;
; ; 24)
; 24)  ;
; ; 26)
; 26) 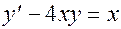 ;
;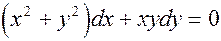 ; 28)
; 28)  ;
; ; 30)
; 30)  ;
; ; 32)
; 32)  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  ;
; ; 18)
; 18)  ;
; ; 20)
; 20) 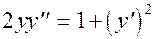 ;
; ; 22)
; 22)  ;
; ; 24)
; 24)  ;
; ; 26)
; 26)  ;
; ; 28)
; 28)  ;
; ; 30)
; 30)  ;
; ; 32)
; 32)  .
. ; y (0)=0;
; y (0)=0;  (0)=0;
(0)=0; ; y (0)=
; y (0)=  ;
;  (0)=
(0)=  ;
; ; y (0)=0;
; y (0)=0;  ; y (0)=1;
; y (0)=1;  ; y (0)=1;
; y (0)=1;  ; y (0)=0;
; y (0)=0;  ; y (0)=1;
; y (0)=1;  ; y (0)=2;
; y (0)=2;  ; y (0)=1;
; y (0)=1;  ; y (0)=3;
; y (0)=3;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0; 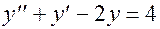 ; y (0)=1;
; y (0)=1;  ; y (0)=0;
; y (0)=0;  ;
; ; y (0)=0;
; y (0)=0;  ; y (0)=4;
; y (0)=4;  ; y (0)=0;
; y (0)=0; 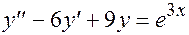 ; y (0)=1;
; y (0)=1;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ;
; ; y (0)=3;
; y (0)=3;  ; y (0)=-1;
; y (0)=-1;  ;
; ; y (0)=2;
; y (0)=2; 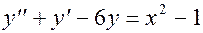 ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  ; y (0)=0;
; y (0)=0;  2)
2) 
 4)
4) 
 6)
6) 
 8)
8) 
 10)
10) 
 12)
12) 
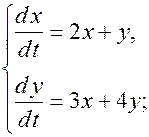 14)
14) 
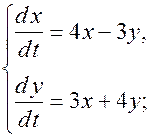 16)
16) 
 18)
18) 
 20)
20) 
 22)
22) 
 24)
24) 
 26)
26) 
 28)
28) 
 30)
30) 
 32)
32) 
 .
.

 .
. .
. .
. (1)
(1) ,
,  . Тоді
. Тоді  ,
,  . Далі за формулою (1) маємо
. Далі за формулою (1) маємо .
.


 .
.
 , dt=dx отримуємо
, dt=dx отримуємо

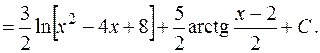
 користувались заміною змінної
користувались заміною змінної  . Тоді
. Тоді  , звідки
, звідки
 .
. .
. ,
, .
. , тоді
, тоді 
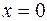 , тоді
, тоді 
 , тоді
, тоді 
 , тоді
, тоді  .
. ,
, ,
,  ,
,  ,
,  .
.
 В знаменнику останнього інтегралу виділимо повний квадрат
В знаменнику останнього інтегралу виділимо повний квадрат  і введемо заміну
і введемо заміну  ,
,  ,
,  :
:
 .
. .
.
 тоді
тоді 
 Отримуємо
Отримуємо
 .
. ,
,
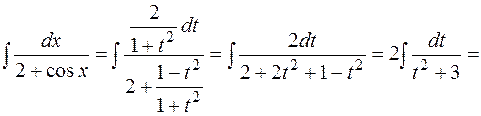
 .
. .
.
 потрібно знайти первісну функцію
потрібно знайти первісну функцію  і замість змінної х спочатку підставити верхню межу b, а потім нижню межу a і від першого результату відняти другий.
і замість змінної х спочатку підставити верхню межу b, а потім нижню межу a і від першого результату відняти другий.
 .
.

 .
. .
.
 .
.



 Площу фігури обчислюємо за формулою
Площу фігури обчислюємо за формулою
 – криві, які обмежують фігуру
– криві, які обмежують фігуру  .
.

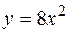 , прямою
, прямою  і віссю Ох.
і віссю Ох.
 або
або 
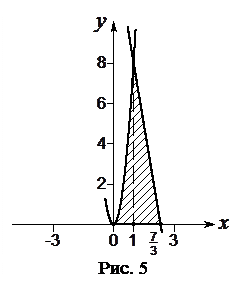 Знаходимо, що
Знаходимо, що  Першій координатній чверті відповідає корінь
Першій координатній чверті відповідає корінь 
 звідки
звідки 
 поверхнею, яка утворена обертанням параболи
поверхнею, яка утворена обертанням параболи  – обертанням прямої
– обертанням прямої 


