
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эволюция факторов производства
Оставшиеся предположения модели задают динамику труда, знаний и капитала. Модель формулируется в непрерывном времени; это означает, что переменные модели определены для любого момента времени[8]. Начальные значения капитала, труда и знаний заданы. Знания и труд растут с постоянными темпами:
где Термин темп роста используется для обозначения скорости относительного приращения. Другими словами, фраза темп роста Одно из ключевых свойств темпа роста состоит в том, что темп роста любой переменной равен скорости изменения натурального логарифма этой переменной. Значит,
Применяя данный результат к уравнениям (1.8) и (1.9), получаем, что скорости изменения логарифмов
где
Следовательно, мы фактически предположили, что Выпуск делится между потреблением и инвестициями. Инвестируемая доля выпуска обозначается через
Никаких специальных ограничений не накладывается на значения Так как это первая модель (из многих!), с которой мы столкнулись, необходимы некоторые комментарии о моделировании в целом. Модель Солоу во многих отношениях очень сильно упрощена. Вот лишь несколько примеров упрощения: рассматривается только одно благо, нет правительства, игнорируются колебания безработицы, производство описывается агрегированной производственной функцией лишь с тремя факторами производства, постоянны нормы сбережений и амортизации, постоянны темпы роста населения и технического прогресса. Вполне естественно думать о таких особенностях модели как о её недостатках: модель упускает из виду многие черты реального мира, причем некоторые из этих черт, без сомнения, важны для роста. Однако модель не строится для того, чтобы быть реалистичной. Более того, у нас уже есть одна совершенно реалистичная модель мира – сам мир. Проблема с этой «моделью» состоит в том, что она слишком сложна для понимания. Модель строится для того, чтобы понять некоторые свойства реального мира. Если упрощение модели приводит к неверному ответу на вопрос, для анализа которого данная модель была построена, тогда недостаточный реализм модели может рассматриваться как её недостаток. (Но даже и такое упрощение, ясно демонстрируя последствия определенных черт реального мира, может быть полезным ориентиром). Если, однако, упрощение не приводит к неверному ответу на вопрос, для анализа которого модель была построена, то нехватка реализма в модели является её преимуществом: выделяя более отчетливо интересующий нас эффект, она делает его более легким для понимания.
Динамика модели Теперь мы хотим определить поведение только что описанной экономики. Эволюция двух из трех факторов производства, – труда и знаний, – задается экзогенно. Следовательно, чтобы определить поведение экономики, мы должны проанализировать поведение третьего фактора, капитала. Динамика Ввиду того, что экономика со временем растет, оказывается значительно проще сосредоточиться на анализе динамики капиталовооруженности эффективного труда
Выражение
Учитывая, что
Выражение (1.18) является основным уравнением динамики модели Солоу. Оно показывает, что изменение капиталовооруженности эффективного труда во времени определяется двумя слагаемыми. Первое слагаемое
Если фактические инвестиции на единицу эффективного труда превышают восстанавливающие инвестиции, то
Рисунок 1.2 Фактические и восстанавливающие инвестиции На рисунке 1.2 изображена зависимость рассмотренных двух слагаемых, задающих Так как
Рисунок 1.3 Фазовая диаграмма для Рисунок 1.3 обобщает полученную информацию посредством фазовой диаграммы, на которой отражена зависимость
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.232 (0.015 с.) |
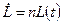 (1.8)
(1.8)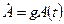 (1.9)
(1.9)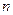 и
и  задаются экзогенно, а точка над переменной используется для обозначения производной по времени (другими словами,
задаются экзогенно, а точка над переменной используется для обозначения производной по времени (другими словами, 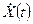 является краткой формой записи для
является краткой формой записи для 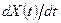 ).
). заменяет выражение
заменяет выражение 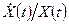 *. Поэтому, из уравнения (1.8) следует, что темп роста
*. Поэтому, из уравнения (1.8) следует, что темп роста 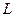 постоянен и равен
постоянен и равен 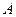 постоянен и равен
постоянен и равен  равняется
равняется 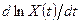 . Чтобы убедиться в этом, заметим, что
. Чтобы убедиться в этом, заметим, что 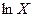 является функцией от
является функцией от  (1.10)
(1.10) , (1.11)
, (1.11) , (1.12)
, (1.12)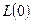 и
и 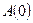 – значения переменных
– значения переменных 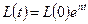 , (1.13)
, (1.13)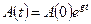 . (1.14)
. (1.14) и является экзогенно заданной постоянной величиной. Единица выпуска, инвестированная в производство, увеличивает запас капитала на единицу. При этом происходит амортизация накопленного капитала с темпом
и является экзогенно заданной постоянной величиной. Единица выпуска, инвестированная в производство, увеличивает запас капитала на единицу. При этом происходит амортизация накопленного капитала с темпом 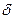 . Таким образом,
. Таким образом,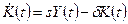 (1.15)
(1.15)
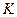 . Так как
. Так как 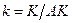 , мы можем применить правило дифференцирования дроби:
, мы можем применить правило дифференцирования дроби: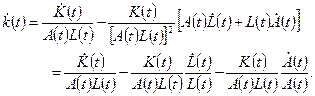 (1.16)
(1.16)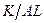 - это просто
- это просто 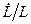 и
и 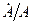 равны, соответственно,
равны, соответственно,  находим из (1.15). Подставив эти выражения в (1.16), получим:
находим из (1.15). Подставив эти выражения в (1.16), получим: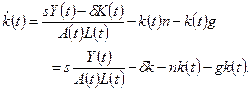 (1.17)
(1.17)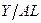 равно
равно 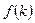 , имеем:
, имеем: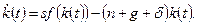 (1.18)
(1.18)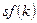 – это фактические инвестиции на единицу эффективного труда. Второе слагаемое
– это фактические инвестиции на единицу эффективного труда. Второе слагаемое 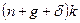 – это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать
– это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать 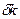 в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала
в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала  недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда
недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда 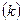 . Эффективный труд растет с темпом
. Эффективный труд растет с темпом  , следовательно, чтобы оставить неизменным
, следовательно, чтобы оставить неизменным 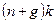 в выражении (1.18).
в выражении (1.18).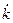 , как функций от
, как функций от 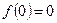 , фактические инвестиции равны восстанавливающим в точке
, фактические инвестиции равны восстанавливающим в точке 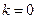 . Из условий Инады следует, что при
. Из условий Инады следует, что при 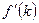 велика, т.е., кривая
велика, т.е., кривая 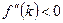 гарантирует, что для
гарантирует, что для 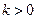 эти линии пересекаются только один раз. Обозначим через
эти линии пересекаются только один раз. Обозначим через  - значение
- значение  . Следовательно, независимо от начального значения,
. Следовательно, независимо от начального значения, 


