Булева алгебра всех подмножеств данного множества.

U = {a1, a2… an) [U] = N [P(U)] = 2n

Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.

Oбъединение эквивалентно V, пересечение - &, дополнение - *, пустое множество – 0, а универсальное – I.

Все аксиомы булевой алгебры справедливы в операциях над множествами.

Булева алгебра характеристических векторов.

Пусть A <= U, A <- P(U)? - характеристический вектор этого подмножества.

?A = {?1,?2..?n) n = [P(U)]

?i = 1, если ai <- A (принадлежит).

?i = 0, если ai не принадлежит A.

U = {1 2 3 4 5 6 7 8 9} A = {2 4 6 8} B = {1 2 7}

?A = {0 1 0 1 0 1 0 1 0}?B = {1 1 0 0 0 0 1 0 0} или

?A = 010101010 – скобки не нужны?A= 110000100

Характеристические векторы размерностью n называются булевыми векторами. Они располагаются в вершинах n – мерного булева куба. Номером булевого вектора является число в двоичном представлении, которым он является

1101 – номер.

Два булевых вектора называются соседними, если их координаты отличаются только в одном разряде (если они отличаются только одной координатой). Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bn.

0 – нулевой вектор. I – вектор из одних единиц.

 

|XY |X&Y |X V Y |

|00 |0 |0 |

|01 |0 |1 |

|10 |0 |1 |

|11 |1 |1 |

Отрицание X = 0 Y = 0 Х = 1 Y= 1

Для размерности n операции над векторами производятся по координатно. Логическая сумма двух векторов – вектор, координаты которого являются логическими суммами соответствующих исходных векторов. Аналогично определено произведение.

Утверждение Между множеством всех подмножеств множества U и булевым кубом Bn, где n= =[U] можно становить взаимное соответствие, при котором операции объединения множества соответствует операции логического сложения (их характеристических векторов), операции пересечения множеств соответствует операция логического умножения их характеристических векторов, а операции дополнения – операция отрицания. Пустому множеству соответствует нулевой вектор, а универсальному – единичный.

Следствие Множество всех характеристических векторов является булевой алгеброй.

Булева алгебра высказываний (алгебра логики)

Высказыванием об элементах множества U называется любое утверждение об элементах множества U, которое для каждого элемента либо истинно, либо ложно.

U = {1 2 3 4 5 6 7 8 9}

A = «число четное» B = «число, меньшее пяти»

Множеством истинности высказывания называется совокупность всех элементов, для которых это высказывание истинно.

SA = {2 4 6 8} SB = {1 2 3 4}

Высказывание, для которого множество истинности пусто, называется тождественно ложным, а для которого SB = U называется тождественно истинным.

Высказывания, для которых множества истинности совпадают, называются тождественными или равносильными. Равносильные высказывания объединим в один класс Р.В. и не будем их разделять, т.к. все они имеют одно и то же множество истинности.

 

Операции над высказываниями

Дизъюнкция высказываний (V, ИЛИ, OR). Дизъюнкция высказываний – высказывание, истинное тогда, когда истинно хотя бы одно из высказываний.

Конъюнкция высказываний (&, И, AND). Конъюнкцией высказываний называется высказывание, истинное тогда и только тогда, когда истинны все высказывания.

Отрицание высказываний (- над буквой, НЕ, NOT). Отрицанием высказывания называется высказывание, истинное только тогда, когда исходное высказывание ложно.

|A B |A & B A V B |Not A |

|Л Л |Л |Л |И |

|Л И |Л |И И |

|И Л |Л |И |Л |

|И И |И |И |Л |

 

Л – ложно.

И – истинно.

Утверждение (основа всей алгебры логики) Между множеством всех классов эквивалентных высказываний об элементах множества U и множеством P(U) можно установить взаимно однозначное соответствие, при котором операция дизъюнкции высказываний соответствует

операции объединения множеств истинности, а конъюнкция соответствует операции пересечения. Операция отрицания соответствует операции дополнения.

ТЕСТОВЫЕ ВОПРОСЫ К ТЕМЕ 3

1. Даны множества: А={3,5,7}и В={0,3,5,7,8} Найдите пересечение множеств А и В.

A) {3,5,7};

B) {3,5};

C) {0,8};

D) {0,3,5,7,8};

E) {7,8}.

2. Даны множества: А={4,6,8,10}и В={7,8,9,10,11}. Найдите объединение множеств А и В.

A) {7,8,9,10,11};

B) {4,6,8,10};

C) {4,6,8,10,7,9,11};

D) {8,10};

E) {4,6,8,10,7,8,9,10,11}

3. Даны множества: А={1,2,3,4,5} и В={1,3,5}. Найдите множество.

A) {1,2,3,4,5};

B) {1,3,5};

C) {2,4};

D) {1,2,3,4,5,1,3,5};

E) {4,5}.

4. Логическое отрицание называется...

A) импликация

B) дизъюнкция

С) эквивалентность

D) конъюнкция

E) инверсия

5. Логтческое умножения – это

A) дизъюнкция

B) импликация

C) инверсия

D) конъюнкция

E) эквивалентность

6.Логическое сложение соответствует союзу...

A) тогда и только тогда, когда если …, то …

B) если …, то …

C) или

D) не

E) и

7. Логическое сложение называется...

A) Эквивалентность

B) Инверсия

C) Импликация

D) Конъюнкция

E) Дизъюнкция

 

8. Логическое умножение обозначается...

A) V

B) <->

C) ->

D) подчеркиванием сверху

E) ^, &

9. Логическое сложение обозначается...

A) <->

B) ^, &

C) ->

D) V

E) подчеркиванием сверху

10. Логика - это...

A) Наука о компьютерах

B) Наука о доказательствах

C) Наука о формах и способах мышления

D) Наука о способах моделирования

E) Наука о построении схем

 

Тема 4. Основы дискретной математики

 

Презентация-Основы логики и логические основы компьютера

 

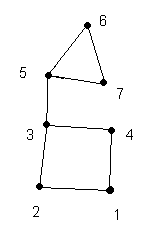
Понятие графа

Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» - пишу.

В математике определение графа дается так:

Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.

Примерами графов могут служить схемы авиалиний, метро, дорог, электросхемы, чертежи многоугольников. Использует графы и дворянство. Например, в генеалогическом дереве, вершины – члены рода, а связывающие их отрезки – отношения родственности. Использует графы и дворянство. На рисунке приведена часть генеалогического дерева знаменитого дворянского рода. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.

 

 

Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Генеалогическое дерево будет деревом и в смысле теории графов, если в этом семействе не было браков между родственниками.

 

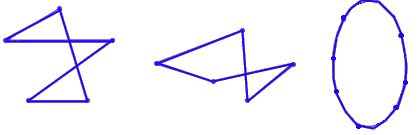
Деревья

Деревом называется любой связный граф, не имеющий циклов. Договорились считать «деревом» и всякий граф, состоящий из одной (изолированной) вершины.

Циклом называется путь, в котором совпадают начало с концом.

Если все вершины цикла разные, то такой цикл называется элементарным (или простым) циклом. Если же цикл включает в себя все ребра графа по одному разу, то такой цикл называется Эйлеровой линией (рис.9а). В графе на рис.9б два цикла: 1-2-3-4-1 и 5-6-7-5.

Путем в графе от одной вершины к другой называется

такая последовательность ребер, по которой можно проложить маршрут между этими вершинами.

При этом никакое ребро маршрута не должно встречаться более одного раза. Вершина, от которой проложен маршрут, называется началом пути, вершина в конце маршрута — конец пути.

Ориентированные графы

Существуют значительные классы практических задач, которые решить с помощью ранее рассмотренных типов графов невозможно. Так, например, схема дорог и площадей города изображается с помощью плоского графа. Но если нужно этой схемой воспользоваться с целью проезда по городу на автомашине, а движение на отдельных (или на всех) улицах одностороннее? Тогда могут помочь сориентироваться в этой ситуации стрелки, расположенные, например, прямо на ребрах-улицах рассматриваемой схемы (графа) города.
Граф, на рёбрах которого расставлены стрелки, называется ориентированным.

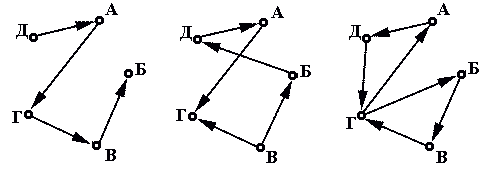
Степенью выхода вершины ориентированного графа называется число ребер, для которых эта вершина является началом (число ребер, «выходящих» из вершины).
Степенью входа вершины ориентированного графа называется число ребер, для которых эта вершина является концом (число ребер, «входящих» в вершину).

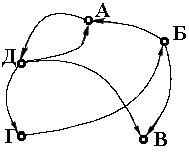
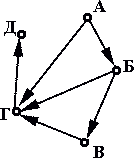
Так, на рисунке 15 изображен ориентированный граф АБВГД. Степени входа и выхода некоторых его вершин такие:

Ст.вх.А=2, Ст.вых.А=1
Ст.вх.В=2, Ст.вых.В=0
Ст.вх.Д=1, Ст.вых.Д=3

Путем, в ориентированном графе от вершины А1 к вершине An называется последовательность ориентированных ребер

A1A2, A2A3,..., Аn-1Аn в которой конец каждого предыдущего ребра совпадает с началом следующего и каждое ребро встречается в этой последовательности только один раз.
На ниже приведенном рисунке показаны примеры путей в ориентированном графе. Причем, первые два пути— простые — ни одна из вершин не содержится в нем более одного раза. Третий путь не является простым, т. к. через вершину Г путь «проходил» дважды.

Ориентированным циклом называется замкнутый путь в ориентированном графе.
На предыдущем рисунке приведены примеры ориентированных циклов в последних двух графах. Цикл, как и любой другой путь в графе, имеет длину, которая определяется числом ребер в этом пути.

Так, на рисунке пути от А к Д могут быть различны и иметь различную длину.
Первый путь имеет длину 2, второй - 3,
а третий — 4.