
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частота события и ее свойстваСтр 1 из 4Следующая ⇒
СОДЕРЖАНИЕ
ВВЕДЕНИЕ Цель курса математики состоит в освоение необходимого математического аппарата. Это необходимо для анализа моделирования и решения прикладных задач, с использованием ЭВМ. Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные процессы.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ Теория вероятностей Теория вероятностей - раздел математики, изучающий закономерности случайных явлений, наблюдаемых при массовых повторениях испытаний. Случайные события Основные понятия. Под испытанием (опытом) понимается осуществление некоторого комплекса условий. Событием назовем всякий факт, который в результате опыта может произойти или не произойти. Событие A в опыте называется достоверным, если при повторениях опыта оно всегда происходит. Событие B в опыте называется невозможным, если при повторениях опыта оно никогда не происходит. Событие в опыте называется случайным, если при повторениях опыта оно иногда происходит, иногда нет. Случайные события обозначаются А, В, С и т.д. Два события называются несовместными (совместными), если появление одного из них исключает (не исключает) появление другого. Несколько событий в данном опыте называются несовместными, если они попарно несовместны. Несколько событий в опыте называются совместными, если совместны хотя бы два из них. События в опыте называются равновозможными, если условия их появления одинаковы и нет оснований считать какое-либо из них более возможным, чем любое другое. Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Пример 1 Опыт - бросание игральной кости; события: А1 - выпадение одного очка, А2 - выпадение двух очков, А3 - выпадение трех очков,
А4 - выпадение четырех очков, А5 - выпадение пяти очков, А6 - выпадение шести очков, В - выпадение четного числа очков, С - выпадение более семи очков, D - выпадение не менее трех очков, E - выпадение не более шести. Достоверное событие в данном опыте - E, невозможное событие - С, остальные события - случайные. Первые шесть событий А1, А2, А3, А4, А5, А6 не могут быть выражены через более простые события и их называют элементарными событиями (элементарными исходами). Кроме того, они образуют полную группу несовместных равновозможных событий. Событие В можно выразить через более простые события: либо наступит А2, либо наступит А4, либо А6; следовательно, элементарным событием событие В не является. Два несовместных события, образующих полную группу, называются противоположными. Противоположные события обозначаются А и Пример 2. Опыт - два выстрела по мишени; события: А - ни одного попадания, Алгебра событий Суммой или объединением событий А1, А2,..., Аn назовем событие, состоящее в появлении хотя бы одного из этих событий. А1+А2+...+Аn=А1ÈА2È...ÈАn. Произведением или пересечением событий А1, А2,..., Аn назовем событие, состоящее в совместном появлении всех этих событий. А1· А2·…·Аn =A1∩A2∩...∩An. Пример 3. Опыт - два выстрела по мишени. Событие Аi - попадание в мишень при i - м выстреле (i =1;2). Тогда событие В=А1+А2 - хотя бы одно попадание, событие С= Частота события и ее свойства Если опыт воспроизведен n раз, а событие А произошло m раз, то частотой (относительной частотой) события А назовем Р*(А)= Свойства частоты. 1) 0≤Р*(А)≤ 1, так как 0≤m≤n, следовательно, 0 ≤ 2) частота достоверного события равна 1, так как m=n. 3) частота невозможного события равна 0, так как m=0. 4) Р*(А+В)=Р*(А)+Р*(В)-Р*(А·В). Условной частотой события В относительно события А, обозначение Р*(В/А), назовем частоту события В при условии, что событие А уже произошло, то есть это число равно отношению числа опытов NAB, в которых произошли события А и В одновременно, к числу опытов NA, в которых появилось событие А, то есть P*(B / A) =
5) Р*(А·В)=Р*(А)·Р*(В/А). Частота случайного события обладает свойством устойчивости, т.е. при увеличении числа опытов значения частоты события группируются около некоторого числа, характеризующего возможность появления данного события в данном опыте. Элементы комбинаторики Имеется совокупность n объектов, назовем ее генеральной совокупностью. Из генеральной совокупности наудачу отбираем m объектов, эту отобранную совокупность назовем выборкой. Выборка может быть упорядоченной, если порядок объектов (элементов) играет роль, и может быть неупорядоченной, если порядок элементов роли не играет. Выборка может быть без повторений, если элементы повторяться не могут, и может быть с повторениями, если элементы в выборке повторяются. Например, телефонный номер 260-61-51 - упорядоченная выборка с повторениями из десяти цифр по семи. Упорядоченная выборка из n элементов по m называется размещением, неупорядоченная выборка из n элементов по m называется сочетанием. Число размещений и сочетаний c повторениями и без повторений из n элементов по m можно найти из следующей таблицы. Таблица 1
Пример 5. Два счета из десяти выполнены с ошибками. Найти вероятность того, что из четырех взятых на проверку счетов один счет окажется с ошибками. Решение. Воспользуемся классической формулой Р(А)=
Запомните: 0!=1. Основные теоремы Следствие 2. Вероятность суммы двух любых событий равна сумме вероятностей этих событий без вероятности их произведения, то есть Р(А+В)=Р(А)+Р(В)–Р(А·В). Замечание. P(A) + P( Теорема умножения. Р(А1·А2·А3·...·Аn)=Р(А1)·Р(А2/А1)·Р(А3/А1·А2) ·...·Р(Аn/А1·А2·А3·...·Аn-1). Правило (теорема) умножения для двух событий. Вероятность произведения двух любых событий равна произведению вероятности одного из них на условную вероятность другого относительно первого, то есть Р(А·В)=Р(А)·Р(В/А)=Р(В)·Р(А/В). Событие А называется независимым от события В, если условная вероятность события А относительно события Bравна безусловной вероятности события А, то есть Р(А/В)=Р(А). Нетрудно доказать, что если А не зависит от В, то и В не зависит от А. Следствие. Если события А и В независимы, то Р(А·В)=Р(А)·Р(В). Пример 6. Студент знает ответы на 20 из 25 вопросов. Какова вероятность того, что он ответит на два выбранных наудачу вопроса? Решение. Рассмотрим события: А- студент знает ответ на первый вопрос, В- студент знает ответ на второй вопрос. Найдем Р(А·В). Р(А·В) = Р(А)·Р(В/А) = Определение. Несколько событий называют независимыми (или независимыми в совокупности), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Следовательно, если А1, А2,...,Аn независимы, то справедливо правило умножения для независимых событий Р(А1·А2·А3·...·Аn)=P(A1)·P(A2)·P(A3)·...·P(An). Пример 7. Два студента выполняют независимо друг от друга задание. Вероятность того, что задание будет выполнено первым студентом 0,6; для второго студента эта вероятность равна 0,8. Найти вероятность того, что
• оба студента выполнят задание; • только один из них выполнит задание; • хотя бы один из них выполнит задание. Решение. События: А - задание выполнит первый студент, В - задание выполнит второй студент. По условию Р(А) = 0,6; Р(В)=0,8; следовательно, Р( • Р(А·В) = /события А и В - независимые события / = Р(А)·Р(В) = 0,6·0,8 = 0,48. • Р(А· • P(A+B)=/ А и В-совместные события /= Р(А)+Р(В)-Р(А·В)=0,6+0,8– –0,48=0,92. Решение.
Теорема 5. Формула Бернулли Производится n независимых испытаний, в каждом из которых событие А наступает с постоянной вероятностью р. Вероятность того, что в этих n испытаниях событие А появится ровно m раз равно Pn(m)= Пример 10. Каждый из пяти независимо работающих элементов отказывает с вероятностью 0,4. Найти вероятность того, что откажут три элемента из пяти. Решение. Р5(3)= Случайные величины Случайной величиной Х в данном опыте называется переменная величина, которая в результате испытания примет одно из своих возможных значений, но какое именно до проведения опыта неизвестно. Совокупность всех возможных значений случайной величины называется спектром. Спектр называется дискретным, если все возможные значения случайной величины образуют конечную или бесконечную последовательность, и называется непрерывным, если все значения случайной величины заполняют сплошь некоторый промежуток. Например, Х - оценка на экзамене. Случайная величина Х имеет дискретный, т.к. ее возможные значения: 2; 3; 4; 5. Или Х - время безотказной работы двигателя. В этом случае случайная величина Х имеет непрерывный спектр, т.к. возможные значения Х заполняют сплошь некоторый промежуток времени [0;t], где t - момент отказа двигателя. Решение. Случайная величина Х может принимать значения: 0; 1; 2.
Условие нормировки: 0,2+0,6+0,2=1. Найдем F(x). Если x из (-∞;0], то F(x)=P(X<x)=0; если x из (0;1], то F(x)=P(X<x)=P(X=0)=0,2; если x из (1;2], то F(x)=P(X<x)=P(X=0)+P(X=1)=0,2+0,6=0,8; если xиз (2;+ ∞), F(x)=P(X<x)=P(X=0)+P(X=1)+P(X=2)=0,2+0,6+0,2=1. Следовательно,
Решение. • Из условия нормировки
Если x из (-∞;2], то F(x)= если x из (2;4], то F(x)= если xиз (4;+ ∞), F(x)= Следовательно,
• Р(0<X<3)= F(3)-F(0)= Решение. Воспользуемся формулой Dx=M[X2]-mx2. Найдем М[X]=(-3)·0,2+(-1)·0,5+2·0,3=-0,5; M[X2]=(-3)2·0,2+(-1)2·0,5+22·0,3=3,5; следовательно,
Dx=3,5-(-0,5)2=3,5-0,25=3,25. Можно вычислить σx = Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ ЗАДАНИЕ №1. Вероятность события. Теоремы сложения и умножения событий.
1. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность выиграть хотя бы один раз, купив 3 билета?
2. У шести животных имеется заболевание, причем вероятность выздоровления равна 0,98. Какова вероятность того, что: а) выздоровят все шестеро животных, б) выздоровят четверо?
3. В магазине работают 2 мужчин и 7 женщин. Трое из них должны пойти в отпуск летом. Кто именно – определяется жребием. Найти вероятность того, что летом в отпуск пойдет хотя бы один мужчина.
4. Среди 10 документов, поступивших в офис, два оформлены с ошибками. Для проверки наудачу взяли 4 документа. Какова вероятность того, что среди ни окажется: а) хотя бы один неверно оформленный документ, б) только один неверно оформленный документ.
5. Рабочий обслуживает 3 станка, каждый из которых работает независимо друг от друга. Вероятность того, что станки потребуют ремонта равна соответственно: 0,4; 0,3; 0,2. Найти вероятность того, что придется ремонтировать все станки. 6. Среди 15 счетов 3 счета оформлены неверно. Ревизор наудачу берет 5 счетов. Найти вероятность того, что среди взятых счетов: а) два оформлены неверно, б) все оформлены верно.
7. В пачке 10 тетрадей, среди них 4 тетради в клетку, а остальные в линейку. Найти вероятность того, что среди наудачу взятых трех тетрадей хотя бы одна будет в клетку.
8. Из 20 методичек по математике 3 по теории вероятностей. Студент наудачу взял две методички. Найти вероятность того, что среди взятых: а) нет методичек по теории вероятностей, б) есть одна методичка по теории вероятностей.
9.Из трех бухгалтеров, восьми менеджеров и шести научных работников необходимо сформировать комитет из 10 человек. Найти вероятность того, что в комитете окажутся: один бухгалтер, пять менеджеров и четыре научных работника.
10.В урне лежат 5 красных, 7 синих и 11 белых шаров. Какова вероятность, что вынутый шар окажется не белым?
ЗАДАНИЕ № 2. Теорема полной вероятности события.
1. Первый рабочий изготовил 40 деталей. Из которых 40 деталей, из которых 4 бракованных. Второй абочий изготовил 30 таких же деталей, из которых 2 бракованных. Все изготовленные детали положены в одну тару и доставлены в ОТК. Найти вероятность того, что деталь, взятая на удачу контролером ТК, соответствует ГОСТу.
2. Сборщик получил 3 ящика деталей: в первом ящике 40 деталей, из них 20 окрашенных; во втором– 50, из них 10 окрашенных; в третьем – 30 деталей, из них 15 окрашенных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
3. На трех пресс-формах изготавливают детали, причем на первой вырабатывается 50% всех деталей; на второй 30% и на третьей – 20%. При этом вероятность появления брака с первой пресс-формы составляет 0,05; со второй – 0,08; с третьей – 0,1. Найти вероятность того, что наудачу взятая деталь, из числа изготовленных, соответствует стандарту.
4.Радиолампа поступает с одного из двух заводов с вероятностью 0,4 и 0,6 соответственно. Вероятность бесперебойной работы лампы составляет: для лампы первого завода – 0,1; второго завода – 0,2. Найти вероятность того, что лампа работает бесперебойно.
5. Фирма имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Известно, что 10% поставляемых фирмой А деталей бракованные, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь будет бракованной?
6. Две литейные машины изготавливают по 250 однотипных отливок в смену, которые хранятся в одном месте. Для первой машины брак составляет 3%, а для второй – 2%. Найти вероятность того, что на удачу взятая отливка будет годной.
7. На сборку поступают детали из трёх заготовительных цехов. Известно, что первый цех даёт 3% брака, второй -2%, третий-1%. Найти вероятность попадания на сборку бракованной детали, если каждый цех поставляет, соответственно, 500, 200 и 300 деталей.
8. На складе хранятся 800 изделий завода №1 и 1200 изделий завода №2. Среди изделий завода №1 в среднем 95% высшего качества, а среди изделий завода №2 – 80%. Чему равна вероятность того, что первое принесённое со склада окажется низкого качества.
9. Трое рабочих за смену изготовили 60 деталей. Производительность рабочих относится как 1:2:3. Первый рабочий изготавливает в среднем 95% годных деталей, второй 85% и третий - 90%. Найти вероятность того, что наудачу взятая из числа изготовленных за смену деталь низкого качества.
10. Среди 100 деталей, изготовленных цехом №1, 85 деталей проходит закалку. Из числа 120 таких же деталей, изготовленных цехом №2, закалку проходят 95 деталей. Все эти детали поступают на сборку. Чему равна вероятность того, что наудачу взятая сборщиком деталь, прошла предварительную закалку?
ЗАДАНИЕ №3. Повторные независимые испытания. Формула Бернулли. Формула Пуассона. Формула Муавра-Лапласа.
1. Вероятность малому предприятию быть банкротом равна 0,2. Найти вероятность того, что из восьми малых предприятий сохранятся: а) два, б) более двух.
2. На факультете насчитывается 1825 студентов. Найти вероятность того, что 1 сентября является днем рождения четырех студентов.
3. В среднем 20% пакетов акций продаются на аукционе по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций по первоначальной цене будет продано: а) менее 2 пакетов, б) хотя бы один пакет.
4. В поселке из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 300 имеют холодильники.
5. Завод отправил на базу 10000 стандартных изделий. Среднее число поврежденных при транспортировке изделий составляет 0,02%. Найти вероятность того, что из 10000 изделий будет повреждено: а) 3, б) менее трех.
6. Предполагается, что 10%новых малых предприятий прекращают деятельность в течение года. Найти вероятность того, что из 6 предприятий 2прекратят деятельность.
7. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 10 договоров с наступлением страхового случая страховая сумма будет выплачена по: а) трем договорам, б) менее двум договорам.
8.Контрольную работу по математике успешно выполняют 70 % студентов. Найти вероятность того, что из 400 студентов работу выполнят 180.
9.Учебник издан тиражом 10000 экземпляров. Вероятность того, что в учебнике есть опечатки равна 0,0001. Найти вероятность того, что тираж содержит: а) 5 бракованных книг, б) менее двух бракованных книг.
10. При проверке установлено, что пятая часть банков имеет уставной фонд свыше 100 млн. руб. Найти вероятность того, что среди 1800 банков такой уставной фонд имеют: а) не менее 300, б)от 300 до 400.
ЗАДАНИЕ №4. Закон распределения вероятностей случайных дискретных величин. Числовые характеристики дискретных случайных величин. Функция распределения вероятностей случайной величины.
1. Вероятность попадания в цель при одном выстреле равна 0,8. Записать закон распределение Х – числа попаданий в цель при 4 выстрелах. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
2. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
3. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Записать закон распределение Х – количества библиотек,которые посетит студент, если в городе 4 библиотеки. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
4. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
5. Студенту задается 3 вопроса. Вероятность ответа на каждый из них составляет 0,9. Записать закон распределение Х – числа ответов студента. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
6. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
7. Клиенты банка не возвращают кредиты с вероятностью 0,1. Составить закон распределения числа Х возвращенных кредитов из 4 выданных. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
8. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
9. Из урны, содержащей 3 белых и 4 черных шара, вынимают на удачу 3 шара. Найти закон распределения Х – числа вынутых черных шаров. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
10. По заданному закону распределения дискретной случайной величины Х: Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
ЗАДАНИЕ №5 Статистическое распределение. Геометрическое изображение. Выборочные характеристики статистического распределения.
По данному статистическому распределению выборки вычислить: а) выборочную среднюю, б) выборочную дисперсию, с) выборочное среднее квадратическое отклонение. Построить полигон частот или гистограмму. 1.
3.
. 5.
6.
7.
8.
9.
10.
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ Основная: 1. Вентцель, Е.С. Задачи и упражнения по теории вероятностей: учеб. пособие для втузов / Е.С.Вентцель, Л.А.Овчаров. - 7-е изд., стер. - М.: Высш. шк., 2006. - 448 с. 2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В.Е. Гмурман. - 9-е изд., стер. - М.: Высш. шк., 2004. - 404 с. 3. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие / В.Е.Гмурман. - 10-е изд., стер. - М.: Высш. шк., 2005. - 404 с.: ил. 4. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В.Е.Гмурман. - 8-е изд., стер. - М.: Высш. шк., 2003. - 404 с. 5. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие / В.Е. Гмурман. - 11-е изд., стер. - М.: Высш. шк., 2005. - 479 с.: ил. 6. Коробейникова, И.Ю. Теория вероятностей. Случайные величины: учеб. пособие / И.Ю.Коробейникова, Г.А.Трубецкая. - Челябинск: АТОКСО, 2004. - 86с. 7. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учеб. для вузов / Н.Ш. Кремер. - 2-е изд., перераб. и доп. - М.: ЮНИТИ, 2006. - 573 с. 8. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов / Н.Ш.Кремер. - М.: ЮНИТИ, 2003. - 543 с. 9. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учебник для студ. вузов / Н.Ш.Кремер. - 3-е изд. - М.: ЮНИТИ, 2007. - 551 с.
Дополнительная: 1. Гнеденко, Б.В. Курс теории вероятностей: учеб. / Б.В.Гнеденко. - 7-е изд., испр. - М.: Эдиториал УРСС, 2001. - 318 с. 2. Емельянов, Г.В. Задачник по теории вероятностей и математической статистике: учеб. пособие / Г.В.Емельянов, В.П.Скитович. - 2-е изд., стер. - СПб.; М.; Краснодар: Лань, 2007. - 331 с. 3. Золотаревская, Д.И. Теория вероятностей. Задачи с решениями: учеб. пособие / Д.И.Золотаревская. - 4-е изд., стереотип. - М.: УРСС, 2006. - 166 с. 4. Кожевников, Ю.В. Теория вероятностей и математическая статистика: учеб. пособие для вузов / Ю.В.Кожевников. - М.: Машиностроение, 2002. - 414 с.Коротков, Е.С. Теория вероятностей и математическая статистика: учебник / Е.С.Коротков, С.О.Смерчинская, В.В.Соколов. – М.: ФОРУМ: ИНФРА-М, 2005. 5. Кочетков, Е.С. Теория вероятностей в задачах и упражнениях: учеб. пособие / Е.С.Кочетков, С.О.Смерчинская. - М.: Форум - Инфра-М, 2005. - 479 с. 6. Красс, М.С. Основы математики и ее приложения в экономическом образовании. Учебник / М.С.Красс, Б.П.Чупрынов – М.: Дело, 2000 7. Розанов, Ю.А. Теория вероятностей, случайные процессы и математическая статистика / Ю.А.Розанов. – М.: Наука, 2000. 8. Свешников, А.А. Прикладные методы теории марковских процессов: учеб. пособие / А.А.Свешников. - СПб.; М.; Краснодар: Лань, 2007. - 189 с. Список вопросов 1. Основные формулы комбинаторики. 2. Классическое определение вероятности. 3. Основные теоремы теории вероятностей. 4. Понятия случайной величины. 5. Числовые характеристики дискретной случайной величины. 6. Непрерывная случайная величина и ее характеристики. 7. Основные законы распределения. 8. Неравенство Маркова. 9. Неравенство Чебышева 10. Центральная предельная теорема. 11. Закон больших чисел. 12. Случайный процесс и его характеристики. 13. Основные понятия теории массового обслуживания. 14. Понятие Марковского процесса. 15. Понятие вариационного ряда и его построение. 16. Показатели вариации. 17. Начальные и центральные моменты вариационного ряда. 18. Типы выборок и способы их отбора. 19. Несмещённость, эффективность и состоятельность оценок. 20. Построение гистограммы и полигонов частот. 21. Доверительные интервалы.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ Цель курса математики состоит в освоение необходимого математического аппарата. Это необходимо для анализа моделирования и решения прикладных задач, с использованием ЭВМ. Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные процессы.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ Теория вероятностей Теория вероятностей - раздел математики, изучающий закономерности случайных явлений, наблюдаемых при массовых повторениях испытаний. Случайные события Основные понятия. Под испытанием (опытом) понимается осуществление некоторого комплекса условий. Событием назовем всякий факт, который в результате опыта может произойти или не произойти. Событие A в опыте называется достоверным, если при повторениях опыта оно всегда происходит. Событие B в опыте называется невозможным, если при повторениях опыта оно никогда не происходит. Событие в опыте называется случайным, если при повторениях опыта оно иногда происходит, иногда нет. Случайные события обозначаются А, В, С и т.д. Два события называются несовместными (совместными), если появление одного из них исключает (не исключает) появление другого. Несколько событий в данном опыте называются несовместными, если они попарно несовместны. Несколько событий в опыте называются совместными, если совместны хотя бы два из них. События в опыте называются равновозможными, если условия их появления одинаковы и нет оснований считать какое-либо из них более возможным, чем любое другое. Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Пример 1 Опыт - бросание игральной кости; события: А1 - выпадение одного очка, А2 - выпадение двух очков, А3 - выпадение трех очков, А4 - выпадение четырех очков, А5 - выпадение пяти очков, А6 - выпадение шести очков, В - выпадение четного числа очков, С - выпадение более семи очков, D - выпадение не менее трех очков, E - выпадение не более шести. Достоверное событие в данном опыте - E, невозможное событие - С, остальные события - случайные. Первые шесть событий А1, А2, А3, А4, А5, А6 не могут быть выражены через более простые события и их называют элементарными событиями (элементарными исходами). Кроме того, они образуют полную группу несовместных равновозможных событий. Событие В можно выразить через более простые события: либо наступит А2, либо наступит А4, либо А6; следовательно, элементарным событием событие В не является. Два несовместных события, образующих полную группу, называются противоположными. Противоположные события обозначаются А и Пример 2. Опыт - два выстрела по мишени; события: А - ни одного попадания, Алгебра событий Суммой или объединением событий А1, А2,..., Аn назовем событие, состоящее в появлении хотя бы одного из этих событий. А1+А2+...+Аn=А1ÈА2È...ÈАn. Произведением или пересечением событий А1, А2,..., Аn назовем событие, состоящее в совместном появлении всех этих событий. А1· А2·…·Аn =A1∩A2∩...∩An. Пример 3. Опыт - два выстрела по мишени. Событие Аi - попадание в мишень при i - м выстреле (i =1;2). Тогда событие В=А1+А2 - хотя бы одно попадание, событие С= Частота события и ее свойства Если опыт воспроизведен n раз, а событие А произошло m раз, то частотой (относительной частотой) события А назовем Р*(А)= Свойства частоты. 1) 0≤Р*(А)≤ 1, так как 0≤m≤n, следовательно, 0 ≤ 2) частота достоверного события равна 1, так как m=n. 3) частота невозможного события равна 0, так как m=0. 4) Р*(А+В)=Р*(А)+Р*(В)-Р*(А·В).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.141 (0.247 с.) |
 (не А).
(не А).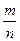 , т.е. отношение числа испытаний, в которых появилось событие А, к числу всех испытаний.
, т.е. отношение числа испытаний, в которых появилось событие А, к числу всех испытаний.

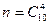 , так как имеем дело с неупорядоченными выборками без повторений, благоприятных из них
, так как имеем дело с неупорядоченными выборками без повторений, благоприятных из них  . Следовательно,
. Следовательно,

 ) = 1–0,8 = 0,2.
) = 1–0,8 = 0,2. .
. .
. =10·0,064·0,36 ≈ 0,23.
=10·0,064·0,36 ≈ 0,23.

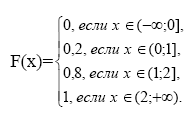

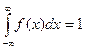 следует
следует , откуда
, откуда  . Итак
. Итак

 =0;
=0; ;
; .
.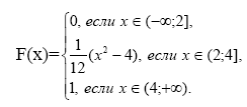

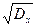 =
=  ≈ 1,80.
≈ 1,80.






