
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи рішення систем лінійних алгебраїчних рівнянь
У програмах аналізу в САПР для рішення СЛАР найчастіше застосовують метод Гауса або його різновиду. Метод Гауса — метод послідовного виключення невідомих із системи рівнянь. При виключенні
всі коефіцієнти
Виключення У загальному випадку число арифметичних операцій для рішення (3.16) по Гаусу пропорційно Можна помітно підвищити обчислювальну ефективність аналізу, якщо використати характерну практично для всіх застосувань властивість високої розрідженості матриці Матрицю називають розрідженою, якщо більшість її елементів дорівнює нулю. Ефективність обробки розріджених матриць велика тому, що, по-перше, перерахування по формулі (3.17) не потрібно, якщо хоча б один з елементів При використанні методів розріджених матриць потрібно враховувати залежність обчислювальної ефективності від того, як представлена матриця коефіцієнтів Для пояснення цієї залежності розглянемо два варіанти подання однієї й тієї ж СЛАР. У першому випадку система рівнянь має вигляд
При прямому ході відповідно до формули (3.17) всі елементи матриці, які спочатку були нульовими, стають ненульовими, а матриця виявляється повністю насиченою. Елементи, що стають ненульовими в процесі гаусових виключень, називають вторинними ненулями. Вторинні ненулі в Табл. 1 відзначені знаком «*». У другому випадку міняються місцями перше й п’яте рівняння. Матриці коефіцієнтів мають вигляд Табл. 1 і Табл. 2, де ненульові елементи представлені знаком «+». Тепер вторинні ненульові елементи не з’являються, матриця залишається розрідженою, висока обчислювальна ефективність зберігається.
Таким чином, методи розріджених матриць повинні містити в собі способи оптимального впорядкування рядків і стовпців матриць. Використовують кілька критеріїв оптимальності впорядкування. Найпростішим з них є критерій розташування рядків у порядку збільшення числа первинних ненулів, більш складні критерії враховують не тільки первинні ненулі, але й вторинні ненулі, що з’являються. Таблиця 1
Таблиця 2
Методом розріджених матриць називають метод рішення СЛАР на основі методу Гауса з урахуванням розрідженості (первинної й вторинної) матриці коефіцієнтів. Метод розріджених матриць можна реалізувати шляхом інтерпретації й компіляції. В обох випадках створюються масиви ненульових коефіцієнтів матриці (з урахуванням вторинних ненулів) і масиви координат цих ненульових елементів. При цьому виграш у витратах пам’яті досить значний. Так, при матриці помірного розміру 200х200 без урахування розрідженості буде потрібно 320 кбайт. Якщо ж взяти характерне значення 9 для середнього числа ненулів в одному рядку, то для коефіцієнтів і покажчиків координат буде потрібно не більше 28 кбайт. У випадку інтерпретації моделююча програма для кожної операції по (3.17) при Спосіб компіляції більше економічний по витратах часу, але уступає способу інтерпретації по витратах пам’яті. При компіляції пошук потрібних для (3.17) коефіцієнтів виконується однократно перед чисельним рішенням задачі. Замість безпосереднього виконання арифметичних операцій для кожної з них компілюється команда зі знайденими адресами ненульових коефіцієнтів. Такі команди утворять робочу програму рішення СЛАР, що і буде вирішуватися багаторазово. Очевидно, що тепер у робочій програмі буде виконуватися мінімально необхідне число арифметичних операцій.
До числа різновидів методу Гауса відноситься метод LU-розкладання, що заснований на розкладанні матриці коефіцієнтів
Крім методу Гауса, для рішення систем лінійних алгебраїчних рівнянь (3.17) застосовують ітераційні методи: метод простої ітерації, метод Зейделя, метод Якобі, методи послідовних верхньої й нижньої релаксації. Наприклад, у методі простої ітерації обчислення виконують по формулі
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.81.94 (0.006 с.) |
 -й невідомої
-й невідомої  із системи рівнянь
із системи рівнянь
 при
при 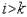 й
й  перераховують по формулі
перераховують по формулі
 невідомих, де
невідомих, де  — порядок системи (3.16), називають прямим ходом, у процесі якого матриця коефіцієнтів здобуває трикутний вид. При зворотному ході послідовно обчислюють невідомі, починаючи з
— порядок системи (3.16), називають прямим ходом, у процесі якого матриця коефіцієнтів здобуває трикутний вид. При зворотному ході послідовно обчислюють невідомі, починаючи з  .
. . Це приводить до значних витрат машинного часу, оскільки СЛАР вирішується багаторазово в процесі одноваріантного аналізу, і істотно обмежує складність аналізованих об’єктів.
. Це приводить до значних витрат машинного часу, оскільки СЛАР вирішується багаторазово в процесі одноваріантного аналізу, і істотно обмежує складність аналізованих об’єктів.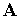 в моделі (3.16).
в моделі (3.16). або
або  виявляються нульовим, по-друге, не потрібні витрати пам’яті для зберігання нульових елементів. Хоча алгоритми обробки розріджених матриць більш складні, але в результаті вдається одержати витрати машинного часу, близькі до лінійних, наприклад, витрати виявляються пропорційними
виявляються нульовим, по-друге, не потрібні витрати пам’яті для зберігання нульових елементів. Хоча алгоритми обробки розріджених матриць більш складні, але в результаті вдається одержати витрати машинного часу, близькі до лінійних, наприклад, витрати виявляються пропорційними  .
.


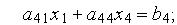

 й
й  знаходить, використовуючи покажчики, потрібні коефіцієнти й виконує арифметичні операції по (3.17). Оскільки СЛАР в процесі аналізу вирішується багаторазово, те й операції пошуку потрібних коефіцієнтів також повторюються багаторазово, на що природно витрачається машинний час.
знаходить, використовуючи покажчики, потрібні коефіцієнти й виконує арифметичні операції по (3.17). Оскільки СЛАР в процесі аналізу вирішується багаторазово, те й операції пошуку потрібних коефіцієнтів також повторюються багаторазово, на що природно витрачається машинний час. й нижню
й нижню 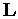 трикутні матриці, що еквівалентно прямому ходу в методі Гауса. Елементи матриць
трикутні матриці, що еквівалентно прямому ходу в методі Гауса. Елементи матриць 

 ,
,  ,
,  . Стовпці матриці
. Стовпці матриці  , починаючи c
, починаючи c  . Після обчислення
. Після обчислення  з матричного рівняння
з матричного рівняння  й, нарешті, вектора
й, нарешті, вектора  з рівняння
з рівняння  .
.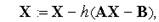
 потрібно вибирати з умови
потрібно вибирати з умови  для будь-якого
для будь-якого  де
де  —
— 


