
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эвольвента зуба колеса, её свойства и уравнение
Образование рабочей эвольвентной поверхности зуба колеса можно представить таким образом. Пусть имеется круглый цилиндр (рис. 8.10, а) с радиусом
Если покатить без скольжения плоскость P по цилиндру, то прямая AB опишет эвольвентную цилиндрическую поверхность, начинающуюся от линии A 0 B 0 касания данной плоскости с цилиндром в начальный момент. В любом сечении эвольвентной поверхности плоскостью, перпендикулярной оси основного цилиндра, получается окружность основания цилиндра с радиусом Образование эвольвенты окружности можно представить как траекторию, описываемую остриём карандаша, привязанного к концу нити, сматываемой с катушки, установленной своей осью перпендикулярно плоскости листа бумаги. Более строго можно сказать, что эвольвента получается как траектория точки прямой линии (производящей прямой), перекатывающейся без скольжения по выпуклой кривой, например окружности. На основанииспособа образования эвольвенты можно так сформулировать её свойства. С в о й с т в а э в о л ь в е н т ы. 1. Нормаль к эвольвенте является касательной к основной окружности. 2. Центры кривизны эвольвенты лежат на основной окружности, так что основная окружность представляет собой эволюту, то есть геометрическое место центров кривизны эвольвенты. 3. Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, 4. Радиус кривизны эвольвенты в данной точке равен дуге основной окружности, заключённой между точкой начала эвольвенты и точкой касания этой прямой с основной окружностью, 5. Правая и левая ветви эвольвенты симметричны. 6. Все точки эвольвенты лежат снаружи от основной окружности.
Для определения полярного угла θ y сначала выразим длину дуги основной окружности через её радиус и центральный угол:
Выразим теперь противолежащий углу α y катет AyCy в ∆OAyCy:
На основании четвёртого свойства эвольвенты имеем
Подставляя в это равенство соответствующие выражения и решая его относительно
В этих математических выражениях и на рис. 8.11 угол θy = invαy. В математических справочниках приводятся таблицы эвольвентной функции, в которых аргумент αy изменяется от нуля до нескольких десятков градусов.
Элементы зубчатого колеса Здесь рассматриваются те элементы колеса, которые относятся к его ободу, где располагаются зубья (рис. 8.12).
Шаг колеса Делительная окружность (её радиус – делит зуб на головку и ножку; – модуль m на этой окружности имеет стандартное значение; – радиус окружности имеет величину – в точке на делительной окружности профильный угол эвольвенты Основная окружность является базовой для образования эвольвенты (от неё начинается эвольвентная часть зуба). Радиус этой окружности получается из рассмотрения прямоугольного треугольника с углом при вершине O, равным
Окружность вершин является габаритной окружностью колеса, её радиус определяется формулой
где Диаметр окружности вершин является диаметром заготовки для изготовления зубчатого колеса. Окружность впадин ограничивает зуб у основания. Её радиус определяется разностью Полная высота зуба, включающая головку и ножку, составляет Контур зуба от основной окружности до окружности вершин очерчен эвольвентой, которая сопрягается с окружностью впадин переходной кривой (для сведения: эквидистантой удлинённой эвольвенты).
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1051; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.87.156 (0.01 с.) |
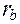 и осью OO, который называется основным цилиндром. Введём в касание с ним плоскость P, содержащую прямую AB, расположенную параллельно образующей цилиндра.
и осью OO, который называется основным цилиндром. Введём в касание с ним плоскость P, содержащую прямую AB, расположенную параллельно образующей цилиндра.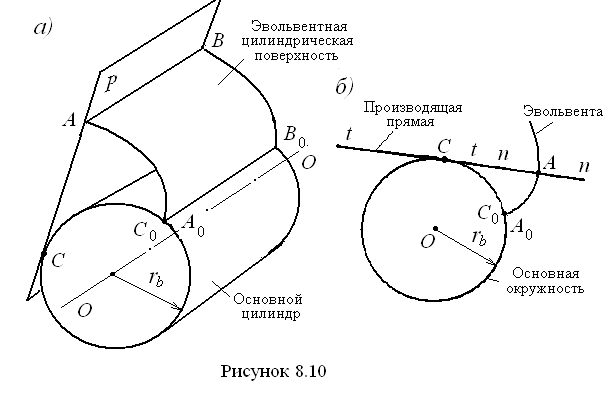
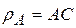 . В точке начала эвольвенты её радиус кривизны равен нулю,
. В точке начала эвольвенты её радиус кривизны равен нулю, 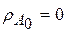 .
.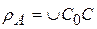 .
.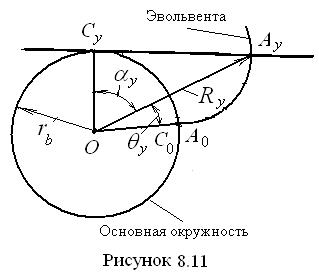 У р а в н е н и е э в о л ь в е н т ы. Для получения уравнения эвольвенты обратимся к рис. 8.11. Положение произвольной точки A y эвольвенты в полярной системе координат определяется двумя координатами относительно её начального радиуса-вектора OA 0 (или OC 0): длиной радиуса-вектора R y и углом θ y. Радиус-вектор Ry определим из прямоугольного треугольника OAyC y:
У р а в н е н и е э в о л ь в е н т ы. Для получения уравнения эвольвенты обратимся к рис. 8.11. Положение произвольной точки A y эвольвенты в полярной системе координат определяется двумя координатами относительно её начального радиуса-вектора OA 0 (или OC 0): длиной радиуса-вектора R y и углом θ y. Радиус-вектор Ry определим из прямоугольного треугольника OAyC y: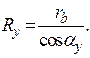
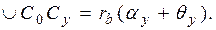
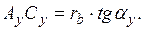
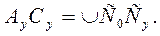
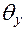 , получаем
, получаем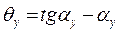 .
. называется профильным углом эвольвенты. Разность между тангенсом какого-либо угла и самим углом называется эвольвентной функцией и обозначается тремя первыми буквами латинского названия эвольвенты involute, то есть inv, так что окончательно уравнение имеет вид:
называется профильным углом эвольвенты. Разность между тангенсом какого-либо угла и самим углом называется эвольвентной функцией и обозначается тремя первыми буквами латинского названия эвольвенты involute, то есть inv, так что окончательно уравнение имеет вид: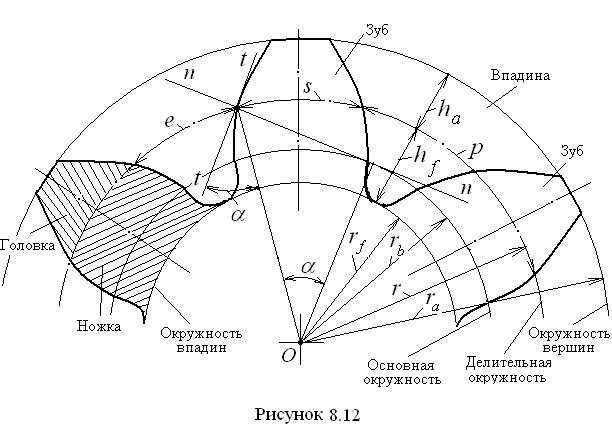 –
– – это расстояние по делительной окружности между одноимёнными профилями двух соседних зубьев,
– это расстояние по делительной окружности между одноимёнными профилями двух соседних зубьев, 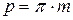 . Шаг включает два параметра – толщину зуба
. Шаг включает два параметра – толщину зуба 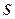 и ширину впадины
и ширину впадины 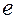 . Если
. Если  , то имеем колесо с равноделённым шагом, в противном случае имеем колесо с неравноделённым шагом.
, то имеем колесо с равноделённым шагом, в противном случае имеем колесо с неравноделённым шагом. ; в зацеплении двух колёс имеет индекс номера колеса):
; в зацеплении двух колёс имеет индекс номера колеса):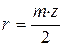 ;
;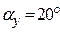 и обозначается буквой
и обозначается буквой 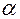 без индекса.
без индекса.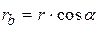 .
.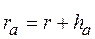 ,
,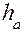 – высота головки зуба, причём
– высота головки зуба, причём 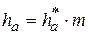 . Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, то есть
. Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, то есть 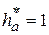 .
.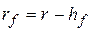 , где
, где 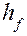 – высота ножки зуба, определяемая равенством
– высота ножки зуба, определяемая равенством  , число
, число 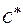 в скобках называется коэффициентом радиального зазора и имеет величину
в скобках называется коэффициентом радиального зазора и имеет величину 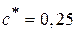 .
.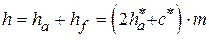 .
.


