Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множественный коэффициент детерминации
Коэффициент множественной детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии. Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными. Для коэффициента множественной детерминации всегда выполняется неравенство вида:
Следовательно, включение в линейную модель регрессии дополнительной факторной переменной xn не снижает значения коэффициента множественной детерминации. Коэффициент множественной детерминации может быть определён не только как квадрат множественного коэффициента корреляции, но и с помощью теоремы о разложении сумм квадратов по формуле:
где ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:
Однако классический коэффициент множественной детерминации не всегда способен определить влияние на качество модели регрессии дополнительной факторной переменной. Поэтому наряду с обычным коэффициентом рассчитывают также и скорректированный (adjusted) коэффициент множественной детерминации, в котором учитывается количество факторных переменных, включённых в модель регрессии:
где n – количество наблюдений в выборочной совокупности; h – число параметров, включённых в модель регрессии. При большом объёме выборочной совокупности значения обычного и скорректированного коэффициентов множественной детерминации отличаться практически не будут.
Парный регрессионный анализ
Одним из методов изучения стохастических связей между признаками является регрессионный анализ. Регрессионный анализ представляет собой вывод уравнения регрессии, с помощью которого находится средняя величина случайной переменной (признака-результата), если величина другой (или других) переменных (признаков-факторов) известна. Он включает следующие этапы:
выбор формы связи (вида аналитического уравнения регрессии); оценку параметров уравнения; оценку качества аналитического уравнения регрессии.
Наиболее часто для описания статистической связи признаков используется линейная форма. Внимание к линейной связи объясняется четкой экономической интерпретацией ее параметров, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. В случае линейной парной связи уравнение регрессии примет вид: Параметры данного уравнения а и b оцениваются по данным статистического наблюдения x и y. Результатом такой оценки является уравнение: Наиболее часто для оценки параметров используют метод наименьших квадратов (МНК). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (u) и независимой переменной (x). Задача оценивания параметров линейного парного уравнения методом наименьших квадратов состоит в следующем: получить такие оценки параметров Формально критерий МНК можно записать так:
Проиллюстрируем суть данного метода графически. Для этого построим точечный график по данным наблюдений (xi,yi, i=1;n) в прямоугольной системе координат (такой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.
Математическая запись данной задачи:
Значения yi и xi i=1; n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров -
В результате получим систему из 2-ух нормальных линейных уравнений:
Решая данную систему, найдем искомые оценки параметров:
Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм (возможно некоторое расхождение из-за округления расчетов). Знак коэффициента регрессии b указывает направление связи (если b>0, связь прямая, если b <0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения. Формально значение параметра а – среднее значение y при х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра а не имеет смысла. Оценка тесноты связи между признаками осуществляется с помощью коэффициента линейной парной корреляции - rx,y. Он может быть рассчитан по формуле:
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:
Область допустимых значений линейного коэффициента парной корреляции от –1 до +1. Знак коэффициента корреляции указывает направление связи. Если rx, y>0, то связь прямая; если rx, y<0, то связь обратная. Если данный коэффициент по модулю близок к единице, то связь между признаками может быть интерпретирована как довольно тесная линейная. Если его модуль равен единице ê rx, y ê =1, то связь между признаками функциональная линейная. Если признаки х и y линейно независимы, то rx,y близок к 0. Для оценки качества полученного уравнения регрессии рассчитывают теоретический коэффициент детерминации – R2yx:
где d 2 – объясненная уравнением регрессии дисперсия y; e 2- остаточная (необъясненная уравнением регрессии) дисперсия y; s 2 y - общая (полная) дисперсия y. Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака y, объясняемую регрессией (а, следовательно, и фактором х), в общей вариации (дисперсии) y. Коэффициент детерминации R2yx принимает значения от 0 до 1. Соответственно величина 1-R2yx характеризует долю дисперсии y, вызванную влиянием прочих неучтенных в модели факторов и ошибками спецификации. При парной линейной регрессии R 2yx=r2 yx.
Производственные функции Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов. Факторами производственной функции могут являться следующие переменные: 1) объём выпущенной продукции (в стоимостном или натуральном выражении); 2) объём основного капитала или основных фондов; 3) объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней);
4) затраты электроэнергии; 5) количество станков, потребляемое в производстве и др. Однофакторные производственные функции (т. е. функции с одной факторной переменной) относятся к наиболее простым производственным функциям. В данном случае результативной переменной является объём производства у, который зависит от единственной факторной переменной х. В качестве факторной переменной может выступать любая из вышеназванных переменных. Основными разновидностями однофакторных производственных функций являются: 1) линейная однофакторная производственная функция вида: y=β0+β1x, например, производственная функция зависимости объёма производимой продукции от величины затрат определённого ресурса. Линейная однофакторная производственная функция характеризуется двумя особенностями: а) если величина факторной переменной х равна нулю, то объём производства у не будет нулевым, потому что y=β0(β0›0); б) объём произведённой продукции у неограниченно возрастает при увеличении затрат определённого фактора х на постоянную величину β1 (β1›0). Однако данное свойство линейной однофакторной производственной функции чаще всего справедливо только на практике; 2) параболическая однофакторная производственная функция вида:
при условиях β0›0, β1›0, β2›0. Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля; 3) степенная однофакторная производственная функция вида:
при условиях β0›0, β1›0. Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений; 4) показательная однофакторная производственная функция вида:
при условиях 0‹β1‹0. Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0. 5) гиперболическая однофакторная производственная функция вида:
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства. Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу.
Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x1,x2)=const, называются изоквантами. Изоквантой называется сочетание минимально необходимых ресурсных затрат для заданного уровня объёма производства. Многофакторные производственные функции используются для изучения зависимости объёма производства от n-го количества факторов производства. Общий вид многофакторной производственной функции: y=f(xi), где
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.37.169 (0.023 с.) |
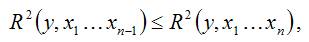




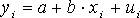
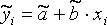 , где
, где  ,
,  - оценки параметров a и b,
- оценки параметров a и b,  - значение результативного признака (переменной), полученное по уравнению регрессии (расчетное значение).
- значение результативного признака (переменной), полученное по уравнению регрессии (расчетное значение). , при которых сумма квадратов отклонений фактических значений результативного признака - yi от расчетных значений –
, при которых сумма квадратов отклонений фактических значений результативного признака - yi от расчетных значений – 


 . Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.
. Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.