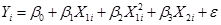Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как, исходя из коэффициента детерминации, проверить гипотезу о значимости линейной связи между переменными.
Коэффициент детерминации R-squared дает предварительную оценку качества модели (от 0 до 1). Он показывает долю объясненной дисперсии зависимой переменной, эквивалентен принципу наименьших квадратов. В практике линейная связь считается значимой, если R-squared (0,6-1). Однако нужно помнить, что слишком высокий R-squared может быть тревожным сигналом (несовершенство связи, например, наличие мультиколлинеарности).. Если R-squared недостаточно высок (0-0,5), значит нужно совершенствовать и дорабатывать модель. Коэффициент детерминации не позволяет дать окончательного заключения без учета других факторов. Он подвержен влиянию посторонних факторов и может привести к ошибочному выводу. Если отсутствуют таблицы для критических значений, на его основе нужно рассчитывать другие показатели. Для чего используется показатель стандартной ошибки уравнения регрессии? Стандартная ошибка – оценка среднего квадратического отклонения значения коэффициента от его истинного значения. Стандартная ошибка указывается для расчета значения t-статистики вручную. Сопоставляя их следующим образом t=b/s.e.(b), мы получаем информацию о значимости регрессии: чем больше t, тем больше шансов, что он окажется значимым. Дополнительно: Стандартная ошибка является оценкой среднего квадратичного отклонения коэффициента регрессии от его истинного значения
Практическая формула расчета стандартной ошибки коэффициента парной регрессии:
Сравнивая значение коэффициента с его стандартной ошибкой, можно судить о значимости коэффициента. Для стандартных ошибок нет таблиц критических уровней – для точного суждения используется t-статистика. Стандартная ошибка необходима для расчета t-критерия. ТЕМА 9. Оценивание нелинейных моделей парной регрессии. В каких случаях можно использовать метод наименьших квадратов для оценивания нелинейных моделей? МНК можно применять к нелинейным регрессионным моделям только в том случае, если они являются нелинейными по независимым переменным или нелинейными по параметрам, но внутренне они линейны, т. е. возможна линеаризация этих моделей (замены нелинейной системы линейной) это возможно с помощью логарифмирования или обратного преобразования (инверсия)
Случайный член - мультипликативный удовлетворяет условиям Гаусса-Маркова, для функции y = αxb. 109. Какие преобразования следует выполнить для оценивания нелинейных моделей Методом наименьших квадратов? 1. Если правая часть уравнения нелинейна по переменным (линейность по переменным означает, что правая часть состоит из взвешенной суммы переменных, а параметры являются весами), то эту нелинейность можно обойти путем замены соответствующих нелинейных переменных. Например:
заменим: тогда: Данное преобразование является лишь косметическим и позволяет избежать лишних обозначений. 2. Если правая часть уравнения нелинейна по параметрам (линейность по параметрам означает, что правая часть состоит из взвешенной суммы параметров, а переменные являются весами), то преобразование в линейную функцию производится путём логарифмического преобразования, использую основные свойства логарифмов (в расчётах используются натуральные логарифмы): a. если b. если c. если d. если Например: Если Если 3. Модели типа: Какие конкретные типы нелинейных моделей пригодны для оценивания Нелинейных моделей методом наименьших квадратов? y=α+b/x и y=αxb, т.е. модели нелинейные по переменным. Все логарифмические зависимости могут быть оценены МНК Функция Кобба-Дугласа может быть приведена к логарифмической зависимости:
МНК применим также для полиномиальных форм:
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.160.14 (0.007 с.) |





 ,то
,то  ;
; ,то
,то 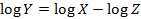 ;
; ,то
,то  ;
; ,то
,то  .
. , то
, то  .
.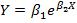 , то
, то  – полулогарифмическая модель (логарифмически-линейная).
– полулогарифмическая модель (логарифмически-линейная). – не могут быть преобразованы в уравнения линейного вида, поэтому в данном случае применение обычной процедуры оценивания модели регрессии невозможно, но для получения оценок параметров по-прежнему применяется принцип минимизации суммы квадратов отклонений.
– не могут быть преобразованы в уравнения линейного вида, поэтому в данном случае применение обычной процедуры оценивания модели регрессии невозможно, но для получения оценок параметров по-прежнему применяется принцип минимизации суммы квадратов отклонений.