
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая теория дисперсии и ее аналитические модели дисперсии оптических постоянных кристаллов.
4.1. История классической теории дисперсии. Дисперсионные уравнения для комплексной диэлектрической проницаемости (аналитические модели Друде и Лоренц-Лорентца) 4.1.1. Аналитическая модель дисперсии диэлектрической проницаемости в приближении отсутствия локального поля (модель Друде) Первая достаточно последовательная аналитическая модель дисперсии комплексной диэлектрической проницаемости (а значит, и оптических постоянных) была развита в конце девятнадцатого века в ходе разработки классической теории дисперсии. Создание этой теории явилось плодом коллективных усилий ряда ученых, среди которых ведущая роль принадлежала Паулю Друде из Германии, Людвигу Лоренцу из Дании и Хендрику Лорентцу (в русской транскрипции часто неточно называемому Генрихом) из Голландии. Диэлектрическая проницаемость диэлектрика Основополагающей идеей классической теории дисперсии явилось рассмотрение смещений связанного электрона по аналогии с колебаниями механического гармонического осциллятора Ньютона. В качестве исходной основы использовалось дифференциальное уравнение Ньютона для вынужденных затухающих колебаний этого осциллятора. В этом уравнении за вынуждающую силу была принята сила, создаваемая электрической составляющей электромагнитного поля световой волны, а роль коэффициента трения играл коэффициент затухания электронного осциллятора. Решение этого уравнения для смещения зарядов использовалось далее для вычисления наведенного дипольного момента и затем через него – поляризуемости:
Здесь e и m –заряд и масса электрона, w – частота электромагнитного поля световой волны, g – коэффициент затухания электронного осциллятора, w 0 – собственная частота электронного осциллятора, определяемая выражением
Найденное таким образом выражение для поляризуемости позволило получить, с помощью соотношения (5), классическое дисперсионное уравнение для комплексной диэлектрической проницаемости. Это уравнение имело следующий вид:
Здесь N – число электронов, возбуждаемых световой волной в единице объема вещества. В уравнении (4.1.2) все электронные осцилляторы полагаются одинаковыми, что представляет собой чрезмерное упрощение. Для набора из J осцилляторов, представляющих собой связанные электроны различных видов, уравнение (4.1.2) преобразуется к виду
где N j и wj – числа в единице объема (N = S N j) и собственные частоты различных электронных осцилляторов (то есть в этом случае символы wj заменяют символ w 0, использовавшийся в вышеприведенном идеализированном случае подобия всех осцилляторов вещества). Действительная и мнимая части комплексной диэлектрической проницаемости, задаваемой уравнением (4.1.3а), имеют вид
и
Классическая аналитическая модель дисперсии комплексной диэлектрической проницаемости в виде (4.1.2) была впервые выведена Паулем Друде. Поэтому для краткости эта модель в виде уравнений (4.1.2-4.1.3в) обычно именуется моделью Друде. Связь классической модели Друде с формулой Зелльмейера. В области прозрачности
Кроме того, в области прозрачности
Отсюда, перенося единицу в левую часть уравнения (4.1.3б) и модифицируя его правую часть в соответствии с вышеуказанными приближениями, получаем вариант формулы Зелльмейера для частот (3.1.6б):
Заменяя w = 2p c / l, w j = 2p c / lj (где lj - дисперсионные длины волн), вводя константы Aj = Sj lj 2/4p2 c 2 и выражая через них Sj как Sj = Aj 4p2 c 2/ lj 2, приходим к первоначальному виду формулы Зелльмейера (3.1.6а):
Таким образом, формула Зелльмейера является упрощенным частным случаем классической модели Друде для области прозрачности. Диэлектрическая проницаемость плазмы свободных зарядов Необходимо также указать частный случай уравнения (4.1.2) для плазмы, то есть среды свободных носителей зарядов. В такой среде на заряды не действует возвращающая сила, и поэтому w 0 = 0. При пренебрежении поглощением диэлектрическая проницаемость сводится к ее действительной части, и соответственно модель Друде для электронной плазмы имеет вид
где w 2 p = 4 pNe 2/ m. Величина wp носит название «плазменная частота», так как вблизи нее наблюдается характерный плазменный минимум коэффициента отражения. Поскольку при w ® wp диэлектрическая проницаемость и соответственно показатель преломления быстро убывают, становясь равными нулю при w = wp, то коэффициент отражения R, задаваемый соотношением (13б), сначала проходит через минимум и затем быстро возрастает до 1.
Некоторые исследователи используют вариант уравнения (4.1.3а), в которое формально введены квадраты парциальных «плазменных» частот w 2 p j = 4 pN j e 2/ m, и для твердых диэлектриков; при этом поглощением не пренебрегается. Тогда уравнение (4.1.3а) принимает вид
В этом случае значения «плазменных» частот w p j не имеют никакого отношения к реальной плазме, а просто соответствуют минимумам диэлектрической проницаемости, следующим за его максимумами (на шкале частот) или предшествующим им (на шкале длин волн). Представление Во многих монографиях (см., например, [1-4]) и лекционных курсах классическое дисперсионное уравнение для комплексной диэлектрической проницаемости представляется только в виде (а) простейших уравнений (4.1.3а-в) или даже (4.1.2), (б) прямо следующих из них уравнений (4.1.4а,б) и (в) нижеследующего уравнения (4.1.8). На самом деле модель Друде, признанная в итоге предпочтительной не только для газов и жидкостей, но и для большинства кристаллов (см. ниже), на протяжении многих последующих десятилетий подвергалась различным модификациям и уточнениям. Наиболее важные из них рассмотрены ниже в параграфе 4.2. 4.1.2. Аналитическая модель дисперсии диэлектрической проницаемости с поправкой на локальное поле (модель Лоренц-Лорентца): Как уже указывалось, напряженность внешнего поля E и напряженность внутреннего поля в материале Eint могут, строго говоря, и не совпадать. В таком случае Eint = E + Eloc, где Eloc - собственное локальное поле в материале, величина которого неизбежно должна зависеть от особенностей состава и структуры материала. Уже упоминавшийся Х. Лорентц вывел аналитическую модель дисперсии диэлектрической проницаемости с учетом локального поля, выведенного из следующей простой физической модели. Если в толще материала, содержащего электрические заряды (например, ионного кристалла) выделить сферическую полость вокруг некоторой частицы и приложить к материалу внешнее электрическое поле, то заряды противоположных знаков вследствие поляризации материала должны сконцентрироваться на противоположных сторонах этой полости. Эти заряды создадут собственное локальное поле Eloc, направленное против приложенного внешнего поля. Для такой простой модели значение Eloc, поддается расчету; оно дается выражением
где В этом случае
и уравнение (1.1.3) превращается в
Это в свою очередь ведет к преобразованию уравнения (4.1.3а) в следующее:
Исходя из других, не столь строгих соображений, к аналогичному уравнению пришел несколько ранее и Л. Лоренц. Поэтому уравнение (4.1.8) широко известно как классическая аналитическая модель дисперсии диэлектрической проницаемости Лоренц-Лорентца (иногда оно называется также уравнением Клаузиуса-Мосотти). В течение достаточно длительного времени было принято считать, что модель Лоренц-Лорентца является более строгой и точной по сравнению с моделью Друде. В дальнейшем с помощью тщательно проведенных теоретических расчетов (см. [17]) выяснилось, однако, что поправка Лорентца очень сильно завышает величину локального поля для веществ с
не вполне ионным характером химической связи, и поэтому в большинстве случаев (кроме, может быть, случая ионных кристаллов) предпочтительнее использовать именно модель Друде, а не модель Лоренц-Лорентца (4.1.8). Несмотря на это, до сих пор даже в серьезных монографиях (например, таких, как [2]) все еще можно встретить утверждение, что модель Лоренц-Лорентца (4.1.8) является наиболее строгим результатом классической теории дисперсии. 4.1.3. Представления о рефракции Понятие «рефракция» (как физическая величина, а не явление) было впервые введено в науку еще в начале восемнадцатого века. Ньютон предложил уравнение, связывающее показатель преломления в видимом диапазоне и плотность r вещества при изменениях температуры и агрегатного состояния вещества:
Эта константа получила наименование удельной рефракции (преломляющей способности) вещества. Для области прозрачности, где действительная часть комплексной диэлектрической проницаемости равна квадрату показателя преломления, разность n 2 – 1 представляет собой действительную диэлектрическую проницаемость согласно уравнению (4.1.3а) модели Друде с перенесенной из правой части единицей. Таким образом, модель Друде как бы придает физический смысл удельной рефракции Ньютона: это (не считая коэффициента 4p) – суммарная электронная поляризуемость одного грамма вещества. Поэтому рефракцию указанного выше вида часто также именуют удельной рефракцией Ньютона-Друде, в связи с чем она обозначается далее символом r ND:
Недостаточная стабильность значений r ND различных веществ при изменениях температуры и агрегатного состояния стимулировала поиск других формул для удельной рефракции, в том числе чисто эмпирических. Например, сначала Бэром для газов и затем Глэдстоном и Дейлом для жидкостей была предложена удельная рефракция (обозначаемая далее символом r GD) следующего вида:
Такая формула рефракции сохраняет физический смысл лишь в случае газов, для которых n» n 2. Тем не менее, она с достаточным успехом применялась не только для жидкостей, но и для стекол. Исходя из соображений, изложенных выше при описании уравнения (4.1.8), Л. Лоренц и Х. Лорентц независимо пришли к формуле для рефракции следующего вида:
которая получила наибольшее распространение среди формул рефракции. Однако ни рефракция Глэдстона-Дейла, ни рефракция Лоренц-Лорентца не дали заметного повышения их стабильности их значений по сравнению с рефракцией Ньютона-Друде при изменениях температуры и агрегатного состояния вещества. Это и понятно, так как строгая стабильность рефракций предполагала бы температурную независимость коэффициентов затухания g, входящих в уравнения (4.1.1), (4.1.2) и (4.1.3а-в), что не соответствует действительности. Напротив, зависимость коэффициентов затухания кристаллов от температуры представляет собой известный и достаточно детально изучавшийся факт, который проявляется в значительном сужении спектральных полос поглощения при переходе от комнатных к температурам жидкого азота или гелия (этот вопрос подробно рассматривается в других дисциплинах). Соответственно и электронные поляризуемости, а, следовательно, и рефракции, неизбежно должны в какой-то степени варьировать с температурой. Еще более заметные изменения поляризуемостей неизбежно должны происходить при изменении агрегатного состояния, так как возникновение кристаллической решетки сопровождается смещением собственных частот и возникновением правил отбора, регулирующих интенсивности отдельных оптических переходов в широких пределах. Поэтому поиски новых вариантов выражений для рефракций, обеспечивающих бóльшую стабильность получаемых значений, продолжались уже на чисто эмпирическом уровне и, как правило, для ограниченных групп веществ (см., например, их обзор в [18]). Определенное развитие идея рефракций получила с введением молярных рефракций R, определяемых выражениями
и
где М – молекулярный вес вещества. Развитие в этом направлении было обусловлено надеждами представить молярную рефракцию вещества в аддитивном приближении как сумму вкладов его ионов, атомов или структурных групп, задаваемых не зависящими от состава инкрементами, и таким образом получить возможность расчета рефракций по составу вещества, используя табулированные значения ионных, атомных или групповых рефракций. В достаточно полной мере эта идея удалась лишь для чисто ионных рефракций щелочных и щелочноземельных металлов, и для ряда групповых рефракций в органических веществах. Это и неудивительно по понятным причинам. Во-первых, разделить на вклады отдельных атомов электронную поляризуемость пары атомов, соединенных химической связью с точно неизвестной степенью ковалентности, практически невозможно. Сильная зависимость молярных рефракций от соотношения ионность-ковалентность обсуждалась, в частности, в [18]. Во-вторых, в формировании диэлектрической проницаемости (а, следовательно, и показателя преломления) при частотах видимого диапазона принимают участие не только электронные возбуждения (как предполагают формы записи уравнений (4.1.1), (4.1.2) и (4.1.3а)), но и колебательные. Таким образом, рефракции оказываются некоторыми суммарными характеристиками как электронных, так и ионных или атомных поляризуемостей вещества с неизвестной долей участия последних, причем эта доля может сильно варьировать от соединения к соединению. Это обстоятельство также усиливает вариабельность молярных рефракций.
Ввиду всего вышеизложенного рефракции не могут считаться величинами, имеющими строгий физический смысл и теоретическую значимость. Однако это не препятствует тому, что они остаются полезными характеристиками для прикладных вычислений, Например, они с успехом могут использоваться в тех случаях, когда нужно ориентировочно оценить изменения показателя преломления в широком температурном интервале (когда эффект термического расширения существенно преобладает над изменениями рефракций) или выбрать наиболее подходящую модель структуры вещества из нескольких возможных на основании данных о его показателе преломления (такой возможностью часто пользуются в органической химии).
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.157.45 (0.021 с.) |
 (4.1.1)
(4.1.1) , где k - силовая постоянная связи в осцилляторе.
, где k - силовая постоянная связи в осцилляторе. . (4.1.2)
. (4.1.2) , (4.1.3а)
, (4.1.3а)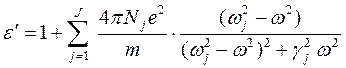 (4.1.3б)
(4.1.3б) (4.1.3в)
(4.1.3в) ; соответственно
; соответственно и
и  .
. , и поэтому
, и поэтому .
. .
.
 , (4.1.4а)
, (4.1.4а) (4.1.4б)
(4.1.4б) диэлектрика в виде (4.1.4б) также достаточно часто встречается в литературе.
диэлектрика в виде (4.1.4б) также достаточно часто встречается в литературе.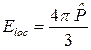 , (4.1.6)
, (4.1.6) - вектор поляризации. Такое значение Eloc принято называть полем или поправкой Лорентца.
- вектор поляризации. Такое значение Eloc принято называть полем или поправкой Лорентца. ,
,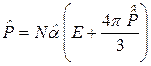 . (4.1.7)
. (4.1.7) . (4.1.8)
. (4.1.8) .
. . (4.1.9а)
. (4.1.9а) (4.1.10а)
(4.1.10а) , (4.1.11а)
, (4.1.11а) , (4.1.9б)
, (4.1.9б) (4.1.10б)
(4.1.10б) , (4.1.11б)
, (4.1.11б)


