
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление произвольной функции алгебры логики в виде формулы алгебры логики
Пусть F(x1,x2,..., хп) - произвольная функция алгебры логики п переменных. Рассмотрим формулу F (1,1,...1) &x1&x2&...&xn
которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции F при некоторых определенных значениях переменных х1, х2,..., хп , остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те итолько те переменные, которые в первом члене конъюнкции имеют значение 0. Вместе с тем формула (1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида. Ясно, что формула (1) полностью определяет функцию F(x1,x2,...,xn). Иначе говоря, значения функции F и формулы (1) совпадают на всех наборах значений переменных x1,x2,...,xn. Например, если х1 принимает значение 0, а остальные переменные принимают значение 1, то функция F принимает значение F (0,1,1,...1). При этом логическое слагаемое F (0,1,1,...1)& Ясно, что вид формулы (1) может быть значительно упрощен, если в ней отбросить те логические слагаемые, в которых первый член конъюнкции имеет значение 0 (и, следовательно, вся конъюнкция имеет значение 0). Если же в логическом слагаемом первый член конъюнкции имеет значение 1, то, пользуясь равносильностью 1& х Таким образом, в результате получается формула (1), которая содержит только элементарные переменные высказывания и обладает следующими свойствами: 1) Каждое логическое слагаемое формулы содержит
все переменные, входящие в функцию F(x1,x2,...,xn). 2) Все логические слагаемые формулы различны. 3) Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание. 4) Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды. Перечисленные свойства будем называть свойствами совершенства или, коротко, свойствами (С). Из приведенных рассуждений видно, что каждой не тождественно ложной функции соответствует единственная формула указанного вида. Если функция F(x1,x2,...,xn) задана таблицей истинности, то соответствующая ей формула алгебры логики может быть получена просто. Действительно, для каждого набора значений переменных, на котором функция F(x1,x2,...,xn) принимает значение 1, запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции xk, если значение xk на указанном наборе значений переменных есть 1 и отрицание xk, если значение xk есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой. Пусть, например, функция F(x1,x2, x3) имеет следующую таблицу истинности:
Для наборов значений переменных (1,1,0), (l,0,l), (0,l,0), (0,0,0), на которых функция принимает значение 1, запишем конъюнкции х1&х2& х1&х2& Закон двойственности Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания. Будем называть операцию конъюнкции двойственной операции дизъюнкции, а операцию дизъюнкции двойственной операции конъюнкции. Определение. Формулы А и А* называются двойственными, если формула А* получается из формулы А путем замены в ней каждой операции на двойственную. Например, для формулы A Теорема. Если формулы А и В равносильны, то равносильны и им двойственные формулы, то есть А* Предварительно докажем лемму.
Лемма. Если для формулы А(х1,х2,...хп) двойственной формулой является А *(х1,х2,...хп), то справедлива равносильность
Доказательство. Для элементарной формулы утверждение леммы очевидно. Действительно, если A(x1) то A*(x1) Пусть теперь утверждение леммы справедливо для всяких формул, содержащих не более k операций. Докажем, что при этом предположении утверждение справедливо и для формулы, содержащей k + 1 операцию. Пусть формула A(x1,x2,...xn) содержит k + 1 операцию. Тогда ее можно представить в одном из трех видов: 1) А(х1,х2,...хп) 2) А(х1,х2,...хп) 3) А(х1,х2,...хп) где формулы А1(х1,х2,...хп) и А2(х1,х2,...хп) содержат не более k операций, и, следовательно, для них утверждение справедливо, то есть
В случае 1) имеем А*
В случае 2) имеем
Аналогичное доказательство проводится и в случае 3). Докажем теперь закон двойственности. Пусть формулы А(х1,х2,...хп) и B(х1,х2,...хп) равносильны: А(х1,х2,...хп) Но тогда, очевидно,
В то же время, согласно лемме,
Из равносильностей (1) и(2) получаем
и, следовательно, А*(х1,х2,...хп) и B*(х1,х2,...хп)
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 976; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.221 (0.013 с.) |

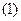
 n
n  x значением формулы (1) является F (0,1.....l).
x значением формулы (1) является F (0,1.....l). A*(
A*( 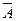 (x1)
(x1)  , А*(
, А*( 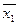 )
)  .
. ,
,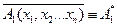 (
( 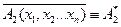 (
( 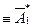 а поэтому
а поэтому
 , апоэтому
, апоэтому
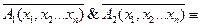
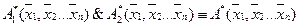

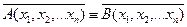


 ,
,


