
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраїчні операції та системи.
Операцією на множині М називається відповідність, при якій з кожною парою елементів з множини М зіставлений певний елемент цієї ж множини. Означена таким способом операція може бути множенням або додаванням і записують. а ·b= c, а + b = c. Приклад: Дія додавання ставить у відповідність парі чисел 2 і 3 число 5. (2; 3) → 5 Операція називається асоціативною для множення і додавання, якщо для будь-яких а, b, c є М виконується співвідношення.
Якщо операція довільна і парі Напівгрупа. Множина М із заданою на ній дією ◦ називається напівгрупою, якщо 1) для кожних 2) дія ◦, задана на М, асоціативна: тобто для кожних елементів 3) існує такий елемент Елемент e – називається нейтральним для дії ◦; для „+” е – називається нульовим; для „ · ” – е називається одиничним елементом.
Приклади. 1) Множина Z – цілих чисел, відносно дії „+” – напівтрупа. 2) Множина Z цілих чисел, відносно дії множення є напівтрупа. 3) Сукупність підстановок множини М: S(M) – є напівгрупою відносно множення. 4) Множина Z+ додатних цілих чисел із заданою операцією Група. Множина М із заданою на ній операцією називається групою, якщо 1) для будь-яких 2) дія ◦ задана на М – асоціативна: 3) існує нейтральний елемент е: 4) для кожного Зауваження: 1) 2) Приклади: 1) Множина Z усіх цілих чисел є група. 2) Множина R+ додатних дійсних чисел відносно множення є група. 3) S(M) – сукупність підстановок множини М є група. 4) Числа -1 і 1 утворюють групу з операцією множення. Кожна група є напівгрупою, але не навпаки. Дії „+” і „ · ” чисел мають властивості комутативності. Але вимога комутативності не входить до означення групи і напівгрупи. Це пояснюється тим, що дія множення перетворень не комутативна, а історичне поняття групи виникло саме на основі вивчення властивості дії множення підстановок.
Група, для якої виконується умова комутативності називається абелевою. Якщо, між елементами двох груп встановлена взаємно-однозначна відповідність, при якій для будь-яких Ізоморфні групи можуть відрізнятися одна від одної лише природою своїх елементів, але всі властивості ізоморфних груп однакові. Множина М називається кільцем, якщо на ній визначені одразу дві операції „+” і „ · ”, причому 1) операція „+” - комутативна 2) операції „+” і „ ◦ ” зв’язані дистрибутивними законами: У кільці може не бути одиниці і обернених елементів. Приклади: 1) Множина Z цілих чисел кільце відносно „+” і „ · ” 2) Множина раціональних чисел Q – кільце відносно „+” і „ · ”. Якщо в кільці для будь-якого Кільця раціональних чисел Q та дійсних чисел R є полями, бо для будь-якого
Перейдемо до більш широкого розкриття змісту поняття групи, бо група є одним з найбільш важливих об’єктів дискретної математики. В загальній теорії група визначається як множина елементів G із заданою на ній двомісною (бінарною) операцією f, що задовольняє певним умовам. Ця операція називається груповою операцією (або груповим законом) (операція f відображає будь-яку пару елементів Групова операція – це функція, що перетворює будь-яку пару елементів множини G у деякий елемент тієї самої множини. При цьому обов’язково зазначають який елемент перший, а який другий. групову операцію позначають +, · або ◦. Групою називається пара < G;f >, яка складається з множини елементів G і двомісної операції f над ними, якщо ця операція задовольняє умовам: 1) операція f асоціативна: 2) існує нейтральний елемент (елемент е множини G, що для будь-яких 3) існує зворотній елемент (тобто для будь-яких Елементи множини G називаються елементами групи.
Умови 1, 2, 3 – називаються аксіомами (первинними істинами). Якщо у групі визначена групова операція „·”, то вона називається мультиплікативною. Якщо у групі визначена групова операція „+”, то така група називається адитивною. Група називається скінченною, якщо у ній скінченна кількість елементів. Група називається нескінченною, якщо у ній нескінченна кількість елементів. Кількість елементів скінченної групи називається порядком. Аксіома асоціативності встановлює порядок перемноження трьох співмножників a, b, c, який може здійснюватись або зліва направо, але за раз заданим порядком. Співмножники, що стоять поряд перемножуються в першу чергу. Потім здійснюється перемноження одержаного результату із співмножником, що залишився. При цьому треба дотримуватись встановленого порядку перемноження, бо результати множення зліва направо і справа наліво можуть відрізнятись. Приклади груп: § число 0 утворює групу за множенням і додаванням: G = {0; +; ·} § число 1 утворює групу за множенням G = {1; ·}
Контрольні запитання. 1. Що таке кортеж?. 2. Що називається довжиною кортежу? 3. Який кортеж називається порожнім? 4. Що називається прямим добутком множин? 5. Що таке відношення? 6. Які є способи задання відношень? (*) 7. Яке відношення називається оберненим? 8. Сформулювати властивості відношень. (*) 9. Що називається відображенням множини А в множину В? 10. Способи задання відображень.(*) 11. Які є види відображень? Їх особливості. (**) 12. Яке відображення називається функцією? 13. Способи задання функції? 14. Що називається перетворенням? 15. Які є види перетворень? 16. Що називається напівгрупою? Наведіть приклади. (**) 17. Що називається групою? Наведіть приклади. (**) 18. Які групи називаються ізоморфними? 19. Яка множина називається кільцем? 20. Що називається полем? Література: О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції5 - 9 Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 1. п. 1.12 – 1.13, розділ 5. п.5.1 - 5.2, 5.5
Розділ 3. Алгебра логіки. План. 1. Висловлення. 2. Основні логічні операції. (*) 3. Основні закони алгебри логіки. (**) 4. Логічні функції. (***) 5. Бульові функції. (***)
Висловлення. Математична логіка – це алгебра висловлень, яка дає простий логічний апарат і відповідну символіку. Свої судження і висновки в повсякденному житті люди передають за допомогою речень. Особливу роль відіграють речення стверджувальні і розповідні, які несуть інформацію і відносно яких можна поставити питання істинне воно чи хибне. Приклади: 1) числа 9 і 37 взаємно-прості; 2) Архімед – англійський математик Можна стверджувати, що приклад 1 є істинним висловленням, а приклад 2 – хибне. Терміни „висловлення”, „істинне висловлення”, „хибне висловлення” належать до неозначуваних понять. Висловлення вивчають тільки з точки зору того, істинні вони чи хибні, зовсім не цікавлячись їхнім конкретним змістом. Висловлювання вважають своєрідною величиною, яке може мати тільки одне значення: „істинне” або „хибне”. Висловлення – зв’язне розповідне речення, про яке модна сказати „істинне” воно або „хибне”.
Будь-яке твердження, що може бути істинним або хибним називається висловленням. Приклади: 1) „ 2×2=4 ” 2) „ 2<3” 3) Річка Дон в 1998 році нашої ери впадає в Каспійське море. 4) „ 5) „Площа відрізка менша довжини куба” 6) Чи є х=3 коренем рівняння 7) Менше один в являється два. 8) Слава російським студентам! 9) „ Висловленнями є приклади 1, 2, 3, 9. при чому 1 і 2 – істинні, а 3 і 9 – хибні. Приклад 5 – не є висловленням, бо про нього не можна сказати істинне воно або хибне (за відсутністю змісту). Приклад 4 – не є висловленням, бо в ньому є змінна, і через неї це речення має властивість перетворюватись в висловлення при фіксації змінної, якщо х= -1, то висловлення 4 – істинне висловлення, якщо х=3, то висловлення 4 – хибне висловлення. Такі приклади є узагальненими прикладами. Приклади 6, 8 –не висловленнями, бо не є розповідними реченнями. Приклад 5 – не висловлення, бо відсутній зміст розповідного речення. Отже, висловлення можуть бути утворені за допомогою слів або символів, але далеко не кожний набір слів або символів є висловленням. Висловлення позначають буквами латинського алфавіту: А,В,С...
Знак Висловлення ділять на прості та складні. Висловлення: А В С Висловлення А, С – істинні, їм приписується значення 1, А Висловлення В – хибне; В З простих висловлень при допомозі так званих логічних зв’язок (союзів „і”, „або”, слів: „якщо..., то...”, „тоді і тільки тоді, коли...”) можна утворювати нові висловлювання які називаються складними: Приклад: Висловлення З висловів А і В можна утворювати слідуючи складні висловлення: С D Е F Зауваження: нові висловлення можна утворювати з таких висловлень, які між собою ніяк не зв’язані по смислу. Наприклад: М (висловлення М – складене за допомогою логічної зв’язки – „якщо..., то...” з двох висловлень, які між собою аж ніяк не зв’язані). В математичній логіці істинність складного висловлення установлюється незалежно від істинності чи хибності простих висловлень з яких вони складені, а на основі зв’язок за допомогою яких вони складені.
Основні логічні операції. Означення логічних функцій дає можливість встановити істинність складного висловлення за значенням істинності його компонентів (складових). Логічні операції застосовують для об’єднання простих висловлень у складні. Основні логічні операції над висловленнями: 1) Операція „Константа – нуль ” – передає висловлення, яке завжди хибне: „ F=0 ”. Приклад: А
2) Операція „Константа – одиниця ” – передає висловлення, яке є завжди істинним: „ F=1 ”. Приклад: В 3) Логічна операція: “Змінна А ” - складневисловлення, яке істинне тоді, коли А - істинне і хибне, коли А – хибне.
4) Логічна операція „ Не” ( заперечення ) – це висловлення яке позначається „F=Ā” і визначається таблицею істинності:
F = Ā – істинне тоді, коли А – хибне і навпаки. Приклад: а) А Ā – означає: неправильно що 5 б) В З операцією заперечення зв’язана тотожність: Тепер перейдемо до бінарних логічних операцій (операцій, які застосовуються до пари висловлень) 5) Логічна операція «Кон’юнкція» (добуток, логічне множення)- називається складне висловлення F=А
Кон’юнкція відповідає союзу „ і ” і має конструкцію „… і ***”. Кон’юнкція має слідуючи властивості: 1) 2) 3) 4)
6) Логічна операція «Диз’юнкція» (логічна сума) – називається складне висловлення „ Диз’юнкція відповідає сполучнику „ або ” і має конструкцію „… або ***”.
Властивості диз’юнкції. 1) 2) 3) 4) 7) Логічна операція „ Імплікація ”, („ якщо-то ”) – називається складне висловлення „ Читається: „якщо А, то В ” або „з А слідує В ”. А – називається умовою імплікації, В – наслідком
Приклад: А В А В Для імплікації мають місце властивості:
1)(а 2) а 3) 0
8) Логічна операція: „ Заборона по В ” (заперечення імплікації А
Читається: „Невірно, що якщо А то В»
9) Логічна операція: „Заборона по А” (заперечення імплікації В
10) Логічна операція: “Еквівалентність” (рівнозначність) -називається складневисловлення „
Еквівалентність відповідає конструкції: „...рівносильно...” або „...тоді і тільки тоді, коли...”. Властивості еквівалентності: 1) а ~ в 2) а ~ в
3) а ~ 1 4) а ~ 0
11) Логічна операція: “Нерівнозначність” - складневисловлення F =А Читається: „ А нерівнозначне до В ”.
12) Логічна операція: “Стрілка Пірса” ( функція Вебба ) - складневисловлення, яке істинне тоді і тільки тоді, коли обидва висловлення А і В хибні: F= Читається: „ні А ні В ”.
13) Логічна операція: “Штрих Шефера” - складневисловлення F=А│В= Читається: „невірно, що А і В ”.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 843; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.202 (0.118 с.) |
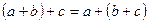
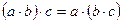
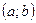 елементів з М вона ставить у відповідність елемент с, то коротко це записують так:
елементів з М вона ставить у відповідність елемент с, то коротко це записують так:  . Елемент с називають композицією.
. Елемент с називають композицією.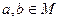 , композиція
, композиція 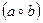 теж належить М;
теж належить М;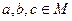 виконується рівність
виконується рівність  ;
;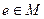 , що для кожного
, що для кожного 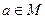 маємо
маємо 
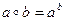 не є напівгрупою.
не є напівгрупою.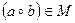
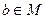 , що
, що 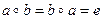
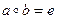 , то для дії „+” - b називається протилежним: а і –а (бо а+(-а)=0), бо їх сума дорівнює нейтральному елементу – 0.
, то для дії „+” - b називається протилежним: а і –а (бо а+(-а)=0), бо їх сума дорівнює нейтральному елементу – 0.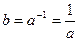 , бо
, бо 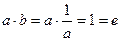 - одиничному елементу.
- одиничному елементу.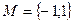
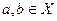 і відповідних їм елементів
і відповідних їм елементів 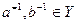 елементу
елементу 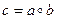 відповідає елемент
відповідає елемент 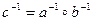 , то такі групи називаються ізоморфними.
, то такі групи називаються ізоморфними.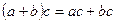 ,
, 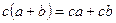
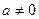 і будь-якого
і будь-якого 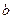 існує рівно один елемент
існує рівно один елемент  такий, що
такий, що 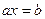 , то таке кільце називається полем, а елемент
, то таке кільце називається полем, а елемент 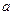 і позначається
і позначається 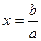 .
.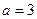
 , тоді
, тоді 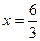
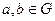 в елемент цієї ж множини).
в елемент цієї ж множини).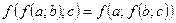
 :
:  )
)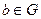 такий, що
такий, що 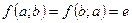 )
)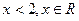 ”, „Дійсне число, менше 2 ”
”, „Дійсне число, менше 2 ” ?
?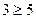 ”
”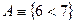 ,
,  .
.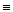 заміняє слова „є висловленням”.
заміняє слова „є висловленням”.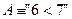 ; і В
; і В 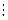 2” – хибне завжди.
2” – хибне завжди.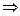 А =0
А =0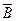
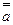
 - закон подвійного заперечення.
- закон подвійного заперечення.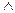 В, яке істинне тоді і тільки тоді, коли істинні обидва висловлення і А і В.
В, яке істинне тоді і тільки тоді, коли істинні обидва висловлення і А і В. - комутативний закон.
- комутативний закон. - закон ідемпотентності.
- закон ідемпотентності.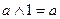
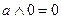
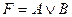 ”, яке істинне тоді і тільки тоді коли істинне хоча б одне із висловлень А і В.
”, яке істинне тоді і тільки тоді коли істинне хоча б одне із висловлень А і В.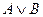
 - комутативний закон
- комутативний закон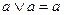 - закон ідемпотентності
- закон ідемпотентності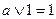
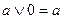
 ”, яке є хибним тоді і тільки тоді, коли А – істинне, В – хибне.
”, яке є хибним тоді і тільки тоді, коли А – істинне, В – хибне.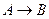
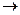 В
В 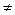 (в
(в 
 ”, яке є істинним тоді і тільки тоді, коли А – істинне, а В – хибне
”, яке є істинним тоді і тільки тоді, коли А – істинне, а В – хибне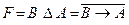 ”,яке є істинним тоді і тільки тоді, коли В - істинне, а А – хибне.
”,яке є істинним тоді і тільки тоді, коли В - істинне, а А – хибне.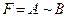 ”, („
”, („  ”) істинне тоді і тільки тоді, коли А=В=1 або А=В=0.
”) істинне тоді і тільки тоді, коли А=В=1 або А=В=0.
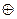 В (А
В (А 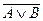 =А
=А 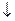 В.
В.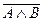 , яке хибне тоді і тільки тоді, коли обидва висловлення істинні.
, яке хибне тоді і тільки тоді, коли обидва висловлення істинні.


