
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства операций на множествах
Определение 5. Бинарная операция ∘ на множестве М называется коммутативной, если Определение 6. Бинарная операция ∘ на множестве М называется ассоциативной, если Пример. Операции Замечание 1. Бинарная операция на множестве М может быть ассоциативной и коммутативной, но не быть алгебраичной. Пример. М= {1, 2, 3}, + - коммутативный и ассоциативный, но 2+3 = 5 Определение 7. Пусть ∘- бинарная алгебраическая операция на множестве М Пример. <ℕ, +>: a +0 = 0+ a = a, но 0 Теорема 11. (Свойство нейтрального элемента). Если во множестве М существует нейтральный элемент относительно бинарной алгебраической операции ∘, то он единственен. Доказательство. Пусть е1, е2 – нейтральные элементы в М относительно операции ∘, покажем, что е1 = е2. Так как е1 – нейтральный элемент относительно операции ∘, то из определения 7 Так как е2 – нейтральный элемент относительно операции ∘, то из определения 7 Из (1) и (2) Определение 8. Пусть ∘- бинарная алгебраическая операция на множестве М Пример. 3 Теорема 12. (свойство симметричного элемента). Пусть∘- бинарная алгебраическая операция на множестве М Доказательство. Пусть a ’ и а ” – симметричные элементы для элемента a Так как а ’ симметричный элемент для элемента a относительно операции ∘, то, по определению 8, а ∘ а ’ = a ’∘ a = e (1).
Так как а ” симметричный элемент для элемента a относительно операции ∘, то, по определению 8, а ∘ а ” = a ”∘ a = e (2). Тогда а ’=(по опр.7)= а ’∘ e =(из (2))= а ’∘(а ∘ а ”)=(ассоциативность ∘) = (a ’∘ a)∘ а ” =(из(1))= е ∘ а ” = (по опр.7)= а ”. Теорема доказана. Определение 9. Пусть ∘,* - бинарные алгебраические операции на множестве М Пример. Умножение дистрибутивно относительно операции + на ℝ; Теорема 13. Пусть∘ -ассоциативная бинарная алгебраическая операция на множестве М Определение 10. Группоид < M,∘> Называется полугруппой, если операция ∘ ассоциативна на М. Определение 11. Полугруппа < M,∘> называется моноидом, если в М существует нейтральный элемент относительно операции ∘. Определение 12. Полугруппа < M,∘> называется полугруппой с сокращением, если из а ∘ с = b ∘ c (c ∘ a = c ∘ b)
Группы. Определение 13. Непустое множество G с определённой на нём бинарной алгебраической операцией ∘ называется группой, если выполняются следующие аксиомы (аксиомы группы): 1) Операция ∘ ассоциативна на G,т. е. а ∘(b ∘ c) = (a ∘ b)∘ c, "a, b, c Î G. 2) В G существует нейтральный элемент относительно операции ∘ т. е. $ e Î G: " a Î G: a ∘ e = e ∘ a = a. 3) Для каждого элемента из G в G существует симметричный ему элемент, относительно операции ∘, т. е. " a Î G $ a' Î G: a∘ a' = a' ∘ a = e. Примеры. <ℕ, +> - не является группой, так как не выполняется аксиома 2) (0 Ï ℕ), но является полугруппой с сокращением; <ℕ, ‧> - не является группой, так как не выполняется аксиома 3) (5 Î ℕ, но 1/5 ∉ ℕ), но является моноидом и полугруппой с сокращением; <ℤ, +> - группа; <ℤ, ‧> - не является группой, так как не выполняется аксиома 3) (5 Î ℤ, но 1/5 ∉ ℤ), но является моноидом и полугруппой с сокращением (для ℤ#);
<ℚ, +>, <ℝ, +> - группы; <ℚ, ‧>, <ℝ, ‧> - не являются группами, так как не выполняется аксиома 3) (для нуля нет обратного); <ℚ#, ‧>, <ℝ#, ‧> - группы. Определение 14. Группа G относительно операции ∘ называется абелевой, если операция ∘ коммутативна на G, т. е. a ∘ b = b ∘ a, " a, b Î G. Определение 15. Группа относительно сложения называется аддитивной. Нейтральный элемент е в ней называется нулевым и обозначается 0. Симметричный элементу а элемент а ’ называется противоположным и обозначается – а. Определение 16. Группа относительно умножения называется мультипликативной. Нейтральный элемент е в ней называется единичным и обозначается 1. Симметричный элементу а элемент а ’ называется обратным и обозначается а -1. Пример. ℤ, ℚ, ℝ – аддитивные группы; ℝ#, ℚ# - мультипликативные группы. Определение 17. Группа G называется конечной, если она содержит конечное число элементов. В противном случае группа называется бесконечной. Определение 18. Порядком конечной группы G называется число элементов группы G, и обозначается | G |. Определение группы можно сформулировать следующим образом: Определение 13'. Непустое множество G с определённой на нём бинарной алгебраической операцией ∘ называется группой, если выполняются следующие аксиомы: 1)' а ∘(b ∘ c) = (a ∘ b)∘ c, "a, b, c Î G. 2)' $ e Î G: a ∘ e = a, " a Î G (e – правыйнейтральныйэлемент ). 3)' " a Î G $ a' ÎG: a∘ a' = e (a' – правыйсимметричныйэлемент ). Покажем, что определение 13 и определение 13' равносильны. Доказательство. 1) Пусть выполняются аксиомы 1) – 3). 1)' – 3)'. Действительно, если G удовлетворяет условиям 1) – 3), то G удовлетворяет условиям 1)' – 3)'. 2) Пусть выполняются аксиомы 1)'–3)'. Покажем, что выполняются 1)–3). Аксиома 1) = аксиоме 1)'. Покажем, что выполняется аксиома 3). Достаточно показать, что a '∘ a = e. Пусть (a ')' – симметричный элемент для a ', тогда по аксиоме 3)': a '∘(a ')' = e, тогда a '∘ a = (a '∘ a)∘ a '∘= (a '∘ a)∘(a '∘(a ')') = a '∘(a∘ a ')∘ (a ')' = (a '∘ e)∘ (a ')' = a '∘(a ')' = e. Таким образом a '∘ a = e => выполняется аксиома 3). Покажем, что выполняется аксиома 2). Достаточно показать, что e ∘ a = a. e ∘ a = (a ∘ a ')∘ a = a ∘(a '∘ a) = a ∘ e = a. Таким образом, e ∘ a = a => выполняется аксиома 2). Следовательно, определения 13 и 13' равносильны. ч. т. д. Замечание. Для группы можно также сформулировать ещё одно определение 13'', в котором вместо правых нейтрального и симметричного элементов рассматриваются левые.
Простейшие свойства групп. Пусть G – мультипликативная группа. Тогда справедливы свойства: 1. Применение операции «⋅» к любым n элементам группы G не зависит от расстановки скобок, и значит, их можно опустить. Доказательство следует из теоремы 13. 2. Пусть a и b Î G, тогда уравнение ax = b (1) (ya = b) имеет в G единственное решение: x = a -1 b (y = ba -1). Доказательство. 1) Докажем, что уравнение (1) имеет в G решение. Таккак a Î G то, поопределению 13аксиома 3), $ a-1 Î G, тогда умножим обе части (1) на а -1 слева: ax = b Þ 2) Покажем, что a -1 b – единственное решение уравнения (1). Пусть x 0 – решение уравнения (1) Þ ax 0 = b – верное равенство. Умножим на a -1 слева. x 0 = a -1 b => x = x 0. Свойство доказано.
3. " a, b, c Î G: ac = bc Þ a = b (ca = cb Þ a = b), т. е. в G выполняется закон сокращения. Доказательство проводится домножением обеих частей равенства ac = bc (ca = cb)на с-1 справа (слева). 4. " a, b, Î G: ab = a Þ b = e. Доказательство. Пусть ab = a Þ ab = ae Þ b=e. 5. " a, b, Î G: (ab)-1 = b -1 a -1. Доказательство. Покажем, что b -1 a -1 является обратным элементом для ab: (ab)(b -1 a -1) = a (bb -1) a -1 = aea -1 = aa -1 = e = 1 Þ b -1 a -1 = (ab)-1. 6. Единичный элемент в группе G определяется однозначно, т. е. он единственен. 7. Для каждого элемента группы симметричный элемент единственен. Доказательство следует из теорем 11 и 12. Замечание. Свойства 1 – 7 для аддитивных групп имеют вид: 1) Применение операции + к любым n элементам группы G не зависит от расстановки скобок, и значит, их можно опустить. 2) Уравнение a + x = b имеет единственное решение: x = - a + b. 3) a + c = b + c Þ a = b. 4) a + b = a Þ b = 0. 5) –(a + b) = (-b) + (-a). 6) Нулевой элемент в группе G определяется однозначно, т. е. он единственен. 7) Для каждого элемента группы противоположный элемент единственен.
|
|||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.150.80 (0.041 с.) |
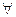 a, b
a, b  М: a ∘ b = b ∘ a.
М: a ∘ b = b ∘ a. и
и  на множестве P (U) являются коммутативными и ассоциативными, + и ‧ на ℤ – ассоциативные и коммутативные.
на множестве P (U) являются коммутативными и ассоциативными, + и ‧ на ℤ – ассоциативные и коммутативные. M.
M.
 , элемент e называется нейтральным элементом относительно операции ∘, если a ∘ e = e ∘ a = a,
, элемент e называется нейтральным элементом относительно операции ∘, если a ∘ e = e ∘ a = a,  0 – нейтральный элемент относительно сложения, но не принадлежит ℕ.
0 – нейтральный элемент относительно сложения, но не принадлежит ℕ. , так как 3×
, так как 3× 


