
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Топологические пространства и топологии.Содержание книги Поиск на нашем сайте Комментарий. Функция Для числовых функций эти определения эквивалентны, поскольку, с одной стороны, множество точек Можно ли дать определение непрерывности для отображения, которое определяется уже не для чисел, а для произвольных носителей, то есть для элементов произвольных множеств? Нет, потому, что неясно, что понимать под окрестностью точки на произвольных носителях.Надо предварительно ввести понятие окрестности точки на произвольном множестве, а потом понятие Множество, на котором корректно введено понятие Для корректного определения понятия окрестности точки в произвольном множестве вспомним, что множество называется открытым, если для любой его точки достаточно малый шар с центром в этой точке (то есть Ранее было показано, что в метрических пространствах для открытых множеств выполняются два свойства: объединение любого (даже бесконечного) набора открытых множеств есть открытое множество и пересечение конечного числа открытых множеств есть открытое множество. Приняв их за аксиомы, получим топологию в аксиоматике Александрова. В силу принципа двойственности топологию можно также задать, описав множество всех замкнутых множеств (т.е. всех дополнений к открытым множествам). Определение 1. Рассмотрим произвольное множество X – носитель топологического пространства. Множество - Все X и пустое множество - Объединение конечного или бесконечного семейства множеств - Пересечение конечного числа множеств Определение 2. Носитель топологического пространства – множество X вместе с заданной на нем топологией Комментарий. Поопределению,все подмножества X, принадлежащие 2.6.1. Способы задания топологии
Задать топологическое пространство – значит задать носитель Х и топологию Примеры 1. Произвольное множество X можно сделать топологическим пространством, если называть открытыми все его подмножества, то есть на любом X включим в топологию вообще все подмножества X (в том числе и все его точки, то есть одноточечные подмножества), само X и пустое подмножество. Такая топология называется дискретной: 2. Второй крайний случай – антидискретная (тривиальная) топология или топология слипшихся точек: на любом носителе X рассмотрим топологию, в которой всего два множества: все X и пустое: 3. Вещественная прямая R является топологическим пространством, если назвать открытыми множествами произвольные (пустые, конечные или бесконечные) объединения конечных или бесконечных интервалов.
4 . Топология Зарисского на числовой прямой. В эту топологию включены вся прямая, пустое множество, и все множества на прямой, дополнения которых до R состоят из конечного числа точек. То есть открытые интервалы получены выбрасыванием из прямой конечного числа точек. 5 . Правая стрелка 6. База Комментарий. Тривиальную и дискретную топологию можно задать, описав все входящие в них множества. С обычной топологией это невозможно, и пришлось описывать ее с помощью свойства, которому удовлетворяют ее множества. Чтобы избежать этого неудобства, было введено понятие базы топологии.
Определение 1. Набор открытых множеств 1) любая точка 2) если точка Пример. Базой обычной топологии на прямой являются Определение 2. Говорят, что топологическое пространство имеет счётную базу, если топология этого пространства имеет базу, состоящую из счетного набора множеств (то есть множества, входящие в эту базу, можно занумеровать натуральными числами). Пример. Обычная топология на прямой имеет счетную базу - это Наследство и сила Комментарий. Топология может наследоваться. Например, в плоскости имеется топология, состоящая из обычных открытых кругов (аналогично случаю числовой прямой). Тогда на любой прямой, лежащей в этой плоскости возникает топология, в которой открытыми множествами являются пересечения с этой прямой и кругов, открытых в плоскости. Эта топология называется индуцированной. В рассматриваемом примере индуцированная топология - это обычная топология на прямой. В некоторых случаях различные топологии на одном и том же множестве можно сравнивать между собой. Определение 1. Топология Пример. Очевидно, что любая топология сильнее тривиальной, а дискретная сильнее любой топологии. Также понятно, что обычная топология сильнее, чем топология Зарисского и чем правая топология. В то же время топологию Зарисского и правую топологию сравнить между собой нельзя - ни одна из них не является более сильной, чем другая. Более того, можно показать, что если некоторое множество числовой прямой входит сразу в обе эти топологии, то это либо вся числовая прямая, либо пустое множество. Непрерывные отображения. Комментарий. Понятие топологии является минимально необходимым для того, чтобы говорить о непрерывных отображениях. Интуитивно непрерывность есть отсутствие разрывов, то есть близкие точки при непрерывном отображении должны переходить в близкие. Оказывается, для определения понятия близости точек можно обойтись без понятия расстояния. Именно это и есть топологическое определение непрерывного отображения. Определение 1. Точкой топологического пространства Определение 2. Окрестностью точки в топологическом пространстве называется любое открытое множество, содержащее указанную точку. Определение 3. Для любого топологического пространства множество Пусть задано отображение Определение 4. Множество Определение 5. Для отображения Комментарий. Следует различать прообраз Пусть задано отображение Определение 6. Отображение
Определение 7. Отображение, непрерывное в каждой точке x множества X, называется непрерывным на X. Если множество X фиксировано, отображения называют просто непрерывными, не указывая X. Примеры. 1. Для произвольных метрических пространств Х и Y постоянное отображение является непрерывным. 2. Тождественное отображение топологического пространства самого на себя является непрерывным. 3. Непрерывную функцию можно рассматривать как непрерывное отображение из топологического пространства R1 в топологическое пространство R1. Теорема 1. (Критерий непрерывности отображения): Отображение
U - окрестность каждой своей точки y = F (x), Достаточность. Теперь пусть для любого открытого множества U топологического пространства Y (то есть Комментарий. Итак, при непрерывном отображении прообраз открытого отображения открыт, а замкнутого замкнут. Для образов при непрерывных отображениях такого рода утверждения, вообще говоря, не имеют место. Примеры.
Определение 8. Непрерывное отображение f: X®Y топологического пространства Х в топологическое пространство Y называется открытым, если при этом отображении образ открытого множества открыт. Определение 9. Непрерывное отображение f: X®Y топологического пространства Х в топологическое пространство Y называется замкнутым, если при этом отображении образ замкнутого множества замкнут. Пример. Тождественное отображение есть пример одновременно открытого и замкнутого отображения. Комментарий. Эта теорема позволяет строить новые топологии. Пусть задан некоторый класс Определение 10. Взаимно - однозначные и взаимно - непрерывные отображение Определение 11. Если существует гомеоморфизм Комментарий. В этом случае мы можем наложить X на Y без самопересечений и разрывов, приклеивая Понятие гомеоморфизма являются центральным для многих разделов топологии, в которых изучаются характеристики, описывающие гомеоморфные, то есть одинаково устроенные пространства, и поэтому их можно считать разными экземплярами одного и того же объекта. Виды топологии Комментарий. Каждое топологическое пространство обладает специфическими свойствами, которые иногда резко отличаются от свойств числовой прямой. Эти свойства есть прямое следствие аксиом отделимости. Основных – пять, потому что числовая прямая с обычной топологией удовлетворяет этим пяти аксиомам. Приведем две важнейшие. А1. Аксиома Колмогорова. У любых двух не совпадающих точек хоть у одной из них существует окрестность, не содержащая другую точку. Комментарий. Очевидно, что для тривиальной топологии эта аксиома не выполняется: в этой топологии есть ровно одно непустое открытое множество - всё X, поэтому всё X будет единственной возможной окрестностью для любой точки и для произвольной пары точек их окрестности совпадают. Все остальные вышеописанные пространства этим свойством обладают. А2. Аксиома Хаусдорфа. Для любых двух не совпадающих точек у каждой из них можно выбрать по окрестности так, чтобы эти окрестности не пересекались. Комментарий. Понятно, что из выполнения аксиомы А2 следует выполнение аксиомы А1,и, значит, если не выполняется аксиома А1, то не выполняется и аксиома А2.Пример1. Числовая прямая с топологией Зарисского не удовлетворяет аксиоме А2. Действительно, в этой топологии открытое множество определяется как множество, дополнение до которого состоит из конечного числа точек, а так как на прямой число точек бесконечно, то любые два открытых множества (в том числе любые две окрестности) пересекаются по бесконечному числу точек. Прямая с обычной и с дискретной топологиями удовлетворяют аксиоме А2. Метризуемость. Определение 1. Топологическое пространство Определение 2. Две метрики Пример 1. Показать, что метрики
Теорема 1. Метризуемое топологическое пространство хаусдорфово.
Предположим, что Пример 2. Топологическое пространство
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

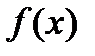 называется непрерывной в точке
называется непрерывной в точке  (по Коши), если для любого
(по Коши), если для любого 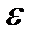 > 0 существует
> 0 существует  =
=  (
( ) > 0, такое, что как только
) > 0, такое, что как только  <
<  , то
, то 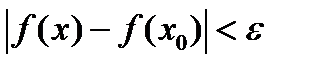 .Удобная модификация: Под окрестностью точки понимается любое открытое множество, содержащее эту точку. Тогдафункция
.Удобная модификация: Под окрестностью точки понимается любое открытое множество, содержащее эту точку. Тогдафункция  существует окрестность V точки
существует окрестность V точки  следует, что
следует, что  .
.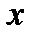 , таких, что
, таких, что  его подмножеств называется топологией на X, если выполнены следующие свойства:
его подмножеств называется топологией на X, если выполнены следующие свойства: принадлежат
принадлежат 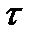 ,
, , принадлежащих
, принадлежащих  , то есть
, то есть 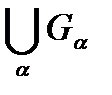 тоже принадлежит
тоже принадлежит  ,
, , то есть
, то есть 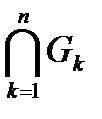 принадлежит
принадлежит  .
. называется топологическим пространством Т=(Х,
называется топологическим пространством Т=(Х,  ).
). , считаются (называются) открытыми множествами. Множества
, считаются (называются) открытыми множествами. Множества  , дополнительные к открытым, называются замкнутыми множествами топологического пространства
, дополнительные к открытым, называются замкнутыми множествами топологического пространства  . Всё множество X и пустое множество
. Всё множество X и пустое множество  , где
, где  - все подмножества множества Х.
- все подмножества множества Х. .
. Действительно, вся числовая прямая очевидным образом открыта, пустое множество включают в число открытых по определению (это непротиворечиво, поскольку в пустом множестве нет точек, тогда можно считать, что каждая из них (!) входит в пустое множество с некоторой
Действительно, вся числовая прямая очевидным образом открыта, пустое множество включают в число открытых по определению (это непротиворечиво, поскольку в пустом множестве нет точек, тогда можно считать, что каждая из них (!) входит в пустое множество с некоторой  -окрестностью). Топологию, состоящую из обычных открытых множеств на числовой прямой, называют нормальной (обычной) топологией. Точно также строится нормальная топология в
-окрестностью). Топологию, состоящую из обычных открытых множеств на числовой прямой, называют нормальной (обычной) топологией. Точно также строится нормальная топология в  . Таким образом,нормальная топология
. Таким образом,нормальная топология  это топология стандартных метрических пространств.
это топология стандартных метрических пространств.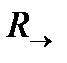 . Эта топология на числовой прямой состоит из всей прямой, пустого множества, и всех открытых интервалов вида
. Эта топология на числовой прямой состоит из всей прямой, пустого множества, и всех открытых интервалов вида  , где a - точка прямой. Аналогично можно задать и левую стрелку.
, где a - точка прямой. Аналогично можно задать и левую стрелку.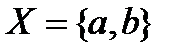 - топологическое двоеточие. Дискретная топология:
- топологическое двоеточие. Дискретная топология:  ,антидискретная топология:
,антидискретная топология:  . На двоеточии возможны ещё две топологии:
. На двоеточии возможны ещё две топологии: 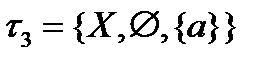 и
и  . Метризуема (то есть можно ввести расстояние) только дискретная топология:
. Метризуема (то есть можно ввести расстояние) только дискретная топология:  Остальные – нет. В случае, например,
Остальные – нет. В случае, например,  открыты
открыты 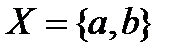 , пустое множество
, пустое множество  , замкнуты
, замкнуты  .
. называется базой топологии
называется базой топологии  в топологическом пространстве Т=(Х,
в топологическом пространстве Т=(Х,  содержится хотя бы в одном
содержится хотя бы в одном  ;
; содержится в пересечении двух множеств
содержится в пересечении двух множеств 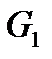 и
и  из
из  , что
, что  .
. -окрестности. Действительно, обычное открытое множество характеризуется тем, что каждая его точка имеет некоторую
-окрестности. Действительно, обычное открытое множество характеризуется тем, что каждая его точка имеет некоторую  -окрестность, входящую в это множество. Очевидно, что само множество есть объединение указанных
-окрестность, входящую в это множество. Очевидно, что само множество есть объединение указанных  -окрестностей всех его точек. Всякое метрическое пространство является топологическим пространством, базу топологии которого составляют открытые шары этого пространства.
-окрестностей всех его точек. Всякое метрическое пространство является топологическим пространством, базу топологии которого составляют открытые шары этого пространства.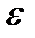 -окрестности с рациональным
-окрестности с рациональным  , центрами которых являются рациональные точки (множество рациональных чисел счетно). Дискретная топология на прямой не имеет счетной базы: в любую базу этой топологии должны входить все точки прямой, а это множество имеет мощность континуума.
, центрами которых являются рациональные точки (множество рациональных чисел счетно). Дискретная топология на прямой не имеет счетной базы: в любую базу этой топологии должны входить все точки прямой, а это множество имеет мощность континуума.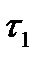 на носителе
на носителе 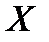 сильнее топологии
сильнее топологии 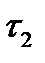 на том же носителе, если все множества, входящие в
на том же носителе, если все множества, входящие в  , входят также и в
, входят также и в  .
.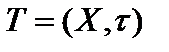 называют любой его элемент.
называют любой его элемент. называется открытым если каждая точка
называется открытым если каждая точка  имеет окрестность
имеет окрестность 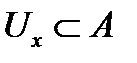 .
. и
и 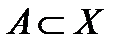 .
. , где
, где  называется образом множества А при отображении
называется образом множества А при отображении  .
. множество
множество  называется прообразом множества В при отображении
называется прообразом множества В при отображении  , инъективно, если
, инъективно, если  и биективно, если оно сюръективно и инъективно.
и биективно, если оно сюръективно и инъективно. , определяемый для любого отображения
, определяемый для любого отображения 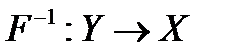 , существующее только для биективных отображений.
, существующее только для биективных отображений. , где
, где 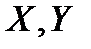 - топологические пространства с топологиями соответственно
- топологические пространства с топологиями соответственно  , если
, если 
 точки
точки 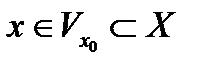 , следует, что
, следует, что  . То есть
. То есть  .
.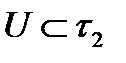 пространства Y его прообраз
пространства Y его прообраз 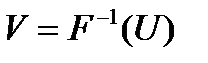 принадлежит
принадлежит 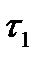 , то есть является открытым множеством топологического пространства X.
, то есть является открытым множеством топологического пространства X. Необходимость. Пусть отображение
Необходимость. Пусть отображение  .
. . Тогда каждое
. Тогда каждое  имеет такую окрестность, что
имеет такую окрестность, что  . Так как, по определению, V есть множество всех точек
. Так как, по определению, V есть множество всех точек  , таких, что
, таких, что 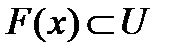 , то
, то  . Так как каждое x принадлежит своему
. Так как каждое x принадлежит своему 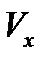 , то объединение всех
, то объединение всех 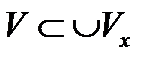 . С другой стороны, все
. С другой стороны, все 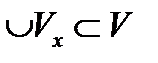 . Из двух включений и следует равенство Таким образом, V есть объединение открытых множеств
. Из двух включений и следует равенство Таким образом, V есть объединение открытых множеств  ) множество
) множество  открыто в X (то есть принадлежит
открыто в X (то есть принадлежит  ). Покажем, что отображение
). Покажем, что отображение  точки F(x) в Y. Это открытое множество, и поэтому
точки F(x) в Y. Это открытое множество, и поэтому  открыто в X по условию. При этом по построению
открыто в X по условию. При этом по построению  . Итак, для любой окрестности
. Итак, для любой окрестности  содержится в
содержится в  Непрерывное отображение f: R1®R1, где f(x)=arctgx, отображает бесконечный интервал R=(-¥, +¥) в интервал
Непрерывное отображение f: R1®R1, где f(x)=arctgx, отображает бесконечный интервал R=(-¥, +¥) в интервал 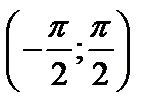 , т.е. открытое и замкнутое множество – в открытое, но не замкнутое множество.
, т.е. открытое и замкнутое множество – в открытое, но не замкнутое множество.  Непрерывное отображение f: R1®R1, где
Непрерывное отображение f: R1®R1, где  отображает открытое и замкнутое множество R=(-¥, +¥) в полуинтервал (0; 1], который не является ни открытым, ни замкнутым множеством.
отображает открытое и замкнутое множество R=(-¥, +¥) в полуинтервал (0; 1], который не является ни открытым, ни замкнутым множеством. подмножеств в X, включив туда множества вида
подмножеств в X, включив туда множества вида  из топологического пространства X в топологическое пространство Y называются гомеоморфизмами.
из топологического пространства X в топологическое пространство Y называются гомеоморфизмами.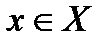 к
к  . Так что получается, что X и Y устроены одинаково.
. Так что получается, что X и Y устроены одинаково.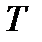 метризуемо, если существует такая метрика
метризуемо, если существует такая метрика 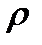 на множестве
на множестве  и
и  на множестве
на множестве  называются эквивалентными, если они порождают на нем одну и ту же топологию.
называются эквивалентными, если они порождают на нем одну и ту же топологию. ,
,  и
и 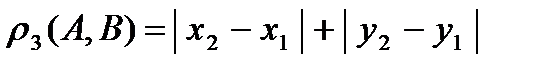 эквивалентны, то есть задают одну и ту же топологию.
эквивалентны, то есть задают одну и ту же топологию.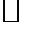 То, что это метрики, было показано ранее. Пусть метрика
То, что это метрики, было показано ранее. Пусть метрика 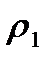 порождает топологию
порождает топологию 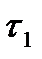 ,
,  - топологию
- топологию  и
и 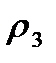 - топологию
- топологию 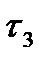 . Достаточно показать два равенства. Покажем, что
. Достаточно показать два равенства. Покажем, что  . Рассмотрим множество
. Рассмотрим множество  , открытое в
, открытое в  открыто в
открыто в 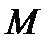 . Шар в
. Шар в  открыто и в
открыто и в  . А тогда и
. А тогда и 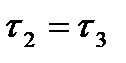 .
.  . Возьмем
. Возьмем 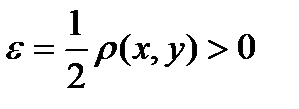 . Докажем, что
. Докажем, что  .
. , тогда существует
, тогда существует  , т.е.
, т.е.  и
и  . Тогда,
. Тогда,  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  .
. 


