
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точками которого остается неизменным.Стр 1 из 10Следующая ⇒
СТАТИКА ЛЕКЦИЯ 1. 1.1 Основные понятия и определения Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел и их систем. Под равновесием в статике будем понимать состояние покоя тела относительно других неподвижных тел. При равновесии тела силы, действующие на него, должны соответствовать определенным условиям равновесия. Формулировка этих условий и написание самих уравнений является основной задачей статики. При ее решении тела считаются недеформируемыми.
Вводятся понятия: Абсолютно твердое тело (АТТ) – тело, расстояние между любыми двумя Точками которого остается неизменным. Свободным называется тело, которому из данного положения можно сообщить любое перемещение в пространстве. В противном случае тело является несвободным.
Наиболее важным понятием в механике является сила – векторная величина, количественно характеризующая взаимодействие материальных тел.
система сил – это некоторая их совокупность, действующая на АТТ.
Система сил может быть плоской, если все силы находятся в одной плоскости; или пространственной, если все векторы системы нельзя поместить в одной и той же плоскости.
Уравновешенной (эквивалентной нулю) называется система, под действием которой Свободное АТТ может находиться в равновесии. Эквивалентными системами сил являются такие системы, под действием которых Тело может находиться в равновесии или совершать Одинаковые движения. Равнодействующей называется сила, эквивалентная по действию данной системе Сил. Аксиомы статики Для вывода уравнений и теорем статики воспользуемся следующими исходными положениями, которые будут приняты без математических доказательств. Эти положения называют аксиомами статики. Аксиома 1: если на свободное АТТ действуют две силы, то тело может находиться в
Равновесии только тогда, когда эти силы равны по модулю, и направлены по одной и той же прямой в противоположные стороны. Аксиома 2: действие данной системы сил на АТТ не изменится, если к нему прило- Жить или снять уравновешенную систему сил.
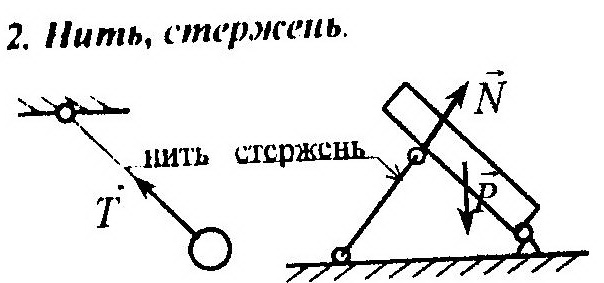
Аксиома 4: при всяком действии одного АТТ на другое имеет место такое же по вели- Чине, но противоположное по направлению противодействие. Связи и их реакции Связями называется все то, что ограничивает перемещение данного тела в пространстве. Силой реакции связи (реакцией связи) называется сила, с которой данная связь Действует на тело, препятствуя тем или иным его перемещениям. Активные силы – это силы, не являющиеся реакциями связей. В основу методов решения задач на равновесие положена аксиома связей: всякое несвободное тело можно рассматривать как свободное, если Отбросить связи и заменить их действие соответствующими силами Реакций. Рассмотрим наиболее часто встречающиеся типы связей:
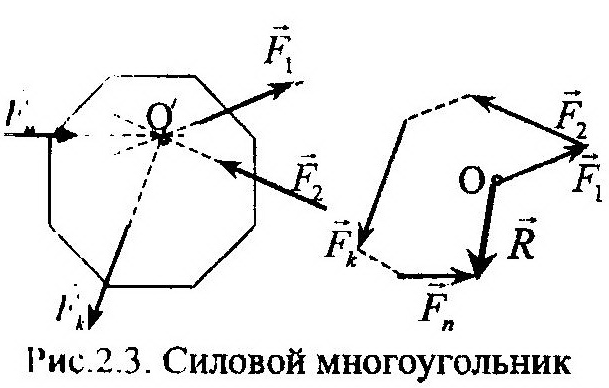
ЛЕКЦИЯ 2. СИСТЕМА СХОДЯЩИХСЯ СИЛ Системой сходящихся сил (ССС) называют такую систему сил, линии действия которых пересекаются в одной той же точке. Геометрический способ сложения сил Главным вектором называется вектор, получаемый путем геометрического Сложения ССС. Сложение двух сил Согласно аксиоме 3, геометрическое сложение осуществляется с помощью правила параллелограмма, что и показано на рисунке 2.1.
Разложение сил.
Разложить силу на составляющие – это означает найти такую ССС, главным Линии действия. Действительно, при переносе силы не меняется ни ее модуль, ни плечо. Поэтому произведение в правой части (2.11) не изменится. 2. Момент силы равен нулю, когда ее линия действия пересекает данный центр. 3. Момент силы численно равен удвоенной площади треугольника OAB, построенного на силе и центре ( рис. 2.6 ), т.е.: m0(F)=2SΔOAB. Действительно,
Сравнивая правую часть полученного выражения (2.12) с формулой момента силы (2.11), заключаем, что площадь треугольника равна половине величины момента силы, что и означает третье свойство момента силы.
Теорема Вариньона Пара сил Сил. ЦЕНТР ТЯЖЕСТИ ТЕЛА КИНЕМАТИКА ЛЕКЦИЯ 6. Кинематикой называют раздел механики, в котором рассматривают движение тел и Векторный способ Данный способ используют, как правило, при выводе теорем и других теоретических положений. Его преимущество перед другими способами – компактность записи. В качестве системы отсчета в этом способе выступает центр О с тройкой единичных векторов – i, j, k (рис. 8.1). Положение в пространстве произвольной точки М определяется посредством радиуса-вектора, r. Таким образом, уравнением движения точки M будет однозначная функция радиуса-вектора от времени, t:
Сравнивая последние два определения, можно заключить, что траектория точки является одновременно годографом ее радиуса-вектора. Введем понятие средней скорости, Vср (рис. 8.1):
и истинной (мгновенной) скорости, V:
Направление V совпадает с касательной, к траектории точки (рис. 8.1). Ускорение точки – это векторная величина, характеризующая изменение скорости точки:
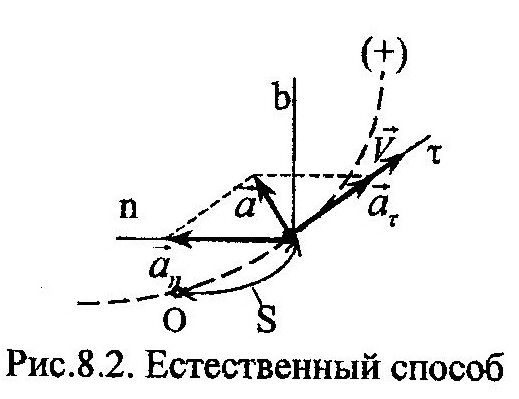
Естественный способ
ная зависимость между S и временем, t, представляет собой уравнение движения точки в естественном способе задания движения:
Скорость точки, направленная по оси t, определяется как:
Ускорение точки, а, находится в плоскости nt и может быть разложено на составляющие:
Физический смысл этого разложения заключается в следующем: линия действия касательной составляющей, аt, совпадает с линией действия вектора скорости, V, и отражает изменение только модуля скорости; нормальная составляющая ускорения, аn, характеризует изменение направления линии действия вектора скорости. Их численные значения могут быть найдены по следующим формулам:
Координатный способ Этот способ наиболее часто используют при решении задач. Системой отсчета является тройка взаимно перпендикулярных осей x, y, z (рис. 8.3). Положение точки М определяется ее координатами xМ, yМ, zМ. Уравнения движения точки представляют собой однозначные функции этих координат от
а ее модуль:
Направление вектора скорости в пространстве можно аналитически определить с помощью направляющих косинусов:
Ускорение точки М можно установить по его проекциям на координатные оси:
Направление вектора ускорения в пространстве определяется направляющими косинусами:
Вращательное движение тела Вращательным называется такое движение тела, при котором хотя бы две его точки Остаются неподвижными. На рис. 9.3 видно, что положение тела при его вращательном движении можно определить
I к подвижной плоскости II, жестко связанной с телом. Однозначная зависимость угловой координаты от времени является уравнением враща-тельного движения:
По формулам (9.6) и (9.7) видно, что определить эти кинематические характеристики тела можно как пределы отношений соответствующих приращений. Выражение для скорости какой-либо точки М тела (рис. 9.3) можно получить из формулы (8.6):
где h – кратчайшее расстояние от точки М до оси вращения. Выражение для касательной, ar, и нормальной, an, составляющих ускорения точки М могут быть найдены с помощью формул системы (8.8):
и
Ускорение точки
Ранее мы показали, что ускорение – это векторная величина, характеризующая изменение вектора скорости. Поэтому естественно предположить, что абсолютное ускорение точки, аа, должно складываться из ускорений относительного, аr, и переносного движений, ае. Однако, как показывает теорема Кориолиса, существует зависимость между относительной и переносной составляющими движения точки. Поэтому абсолютное ускорение точки, при ее сложном движении, будет складываться из трех составляющих:
Последнее слагаемое, ускорение Кориолиса учитывает влияние относительного движения точки на пере- носную скорость и влияние переносного движения на относительную скорость:
где ωе – угловая скорость переносного движения. Из (10.3) его модуль:
Направление вектора ас можно установить либо на основе правила векторного произведения, либо с помощью следующей процедуры, показанной на рис. 10.2:
та, т.е. подвижная система отсчета движется поступательно. 2) Vr=0 (относительная скорость равна нулю) – означает, что относительное движение точки имеет место, но в какие-то моменты времени частные значения скорости равны нулю. Пример такого случая приведен на рис. 10.3. Здесь точка М (шар) совершает сложное движение относительно неподвижной точки О. Движение точки М относительно
раллелен вектору относительной скорости) – означает, что на протяжении всего движения или в какие-то моменты времени эти векторы ориентированы параллельно друг другу.
ДИНАМИКА ЛЕКЦИЯ 11 11.1. Основные понятия и определения Динамикой называется раздел теоретической механики, в котором рассматривается Законы механики
В основе классической механики лежат следующие законы, впервые изложенные И. Ньютоном в работе «Математические начала натуральной философии» (1687г.).
1. Закон инерции: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Данный закон позволяет поделить все системы отсчета на инерциальные и неинер-циальные. Инерциальными системами отсчета являются такие системы, где выполняется за- кон инерции; в противном случае, системы отсчета являются неинерциальными.
2. Основной закон динамики: произведение массы материальной точки на ее ускорение, которое она получает под действием силы, равно модулю этой силы, и направление ускорения совпадает с направлением вектора силы.
Из этого закона видно, что мерой инертности точки является ее масса. Действительно, при действии на две точки одинаковыми силами ускорение той точки будет меньше, у которой масса больше. Следует заметить, что второй закон удобнее использовать в следующей форме записи:
Действительно, на точку одновременно действуют несколько сил, образуя систему сходящихся сил. Их равнодействующая F и представлена в правой части выражения ос-
Здесь знак «-» указывает на противоположность направлений двух равных по модулю векторов, стоящих по обе стороны равенства. Следует заметить, что хотя геометрическая
Следует заметить, что для скорости точки аналогичная суперпозиция не имеет место.
ДИНАМИКА ТОЧКИ Уравнения движения точки
В зависимости от способа описания движения точки для решения задач используют различные формы записи уравнений. Получим дифференциальные уравнения движения точки в координатной и естественной формах. Задачи динамики
Все задачи динамики можно условно поделить на две группы: первая (прямая) и вторая (обратная) задачи. Условность деления заключается в том, что не все задачи один к одному соответствуют формулировкам, указанным ниже. Возможно и их сочетание в пределах одной задачи. В прямых задачах: по известным уравнениям движения точки определяют силы,вызы- Вающие его. Таким образом, исходными для решения первой задачи динамики точки являются ее уравнения движения, записанные в одном из видов: векторном, координатном или естественном (см. тему: «способы задания движения точки»). Например, в координатной форме записи эти уравнения связывают координаты точки (x, y, z) с временем (t). Алгоритм решения первой (прямой) задачи представлен ниже:
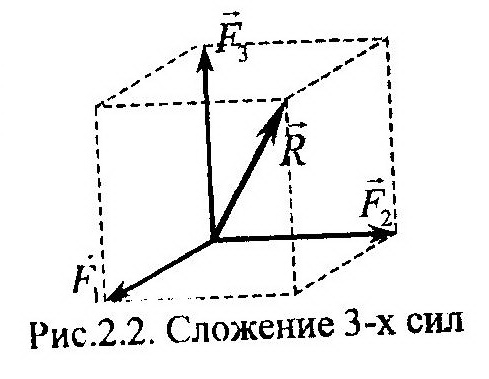
По известным уравнениям движения находят вторые производные от координат по времени и, умножая их на массу точки, m, определяют правые части выражений (12.2). Модуль равнодействующей, R, системы сходящихся сил, приложенных к точке, равен длине диагонали параллелепипеда, построенного на проекциях Rx, Ry, Rz как на сторонах. С помощью направляющих косинусов можно определить направление вектора равно-действующей в пространстве.
В обратных задачах: по известным силам, действующим на точку, и начальным усло- Классификация сил
Механической системой называется такая совокупность материальных точек или тел, положение и движение которых взаимосвязаны. Таким примером является Солнечная система, где каждое тело (планета, например) имеет свою определенную достаточно устойчивую траекторию движения. Применительно к механической системе силы делятся на внутренние и внешние. Внутренними называются силы взаимодействия между точками или телами одной и Ляется следующими формулами В векторном способе:
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Ния механической системы.
Механической системы Рассмотрим механическую систему, состоящую из n материальных точек (рис. 13.2). Для вывода данной теоремы воспользуемся системой дифференциальных уравнений (13.6). Сложим почленно эти уравнения, получим:
Последняя сумма в (14.19) равна нулю по 1-му свойству внутренних сил. Левую же часть можно преобразовать следующим образом:
Учитывая (14.20), перепишем (14.19) в виде:
что и представляет собой векторную форму записи теоремы об изменении количества движения механической системы в дифференциальной форме, т.е.: производная по времени от количества движения механической системы равна геометрической сумме всех внешних сил, действующих на эту систему. В скалярной форме эта теорема может быть записана в проекциях на координатные оси:
В конечном виде выражение теоремы можно получить как из выражения (14.21), так и из (14.22). Для этого необходимо разделить переменные и проинтегрировать эти выражения, получим:
или
Саму теорему на основе (14.24) можно формулировать следующим образом: Моменты количества движения Механической системы
Главным моментом количеств движения механической (кинетическим моментом) называется геометрическая сумма моментов количеств движения материальных точек данной системы:
Аналогично (14.40) определяются кинетические моменты системы относительно координатных осей:
Если количество движения системы, Q, характеризует поступательную составляющую движения механической системы, то кинетический момент, К, - ее угловое перемещение. Очевидно, что выражения (14.40) и (14.41) неудобны для вычисления кинетических моментов, поскольку они подразумевают длительный процесс суммирования. При вращательном движении тела можно предложить удобную форму вычисления данной характеристики. На рис. 14.6 представлено тело, совершающее вращательное движение относительно неподвижной оси z. Найдем Kz для данного случая, для чего запишем момент количества движения произвольной точки М относительно оси z. Получим:
Для достижения цели воспользуемся выражением (14.41). Подставив в него (14.42),
(14.18). Действительно, кинетический момент и количество движения являются динамическими характеристиками механической системы. Они определяются как произведение меры инертности на скорость. В случае расчета величины количества движения, характеризующей поступательную составляющую движения системы, используется масса и линейная скорость, а при определении кинетического момента – момент инерции и угловая скорость. Структура этих выражений следующая:
Работа силы
Понятие работы силы связывает два фундаментальных понятия: сила и энергия. Введем сначала понятие элементарной работы силы:
ся положительный, если угол α между вектором силы, F, и скоростью, V, точки приложе-ния силы – острый. В противном случае, работа силы будет отрицательной. Другими словами, если сила увеличивает модуль скорости, то работа этой силы положитель-ная, и наоборот. Выражение (14.48) используют при естественном способе задания движения точки. При использовании векторного способа параметр, определяющий положение точки, является радиус-вектором, r. Нетрудно показать, что элементарное изменение дуговой координаты, dS, эквивалентно элементарному перемещению, dr. Тогда, используя (14.49), получим:
т.е. элементарная работа силы равна скалярному произведению вектора силы на век- Работа силы тяжести
Пусть точка М движется по некоторой траектории под действием силы тяжести Р (РИС. 14.9). Определим работу этой силы на перемещении М0М1. Воспользуемся выражением (14.52), получим:
(14.54) следует, что значение работы силы тяжести не зависит от вида самой траектории. Силы, обладающие таким свойством, называются потенциальными.
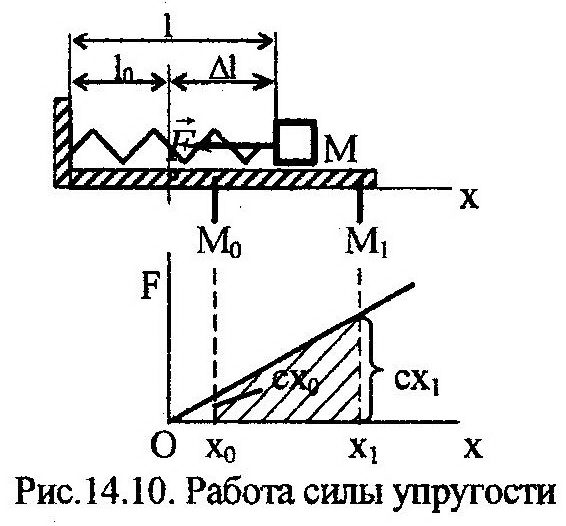
Работа силы упругости
Примером такой силы является реакция пружины на ее деформацию. На рис. 14.10 показано тело М, к которому крепится пружина длиною l0.
где Δl0, Δl1 – начальная и конечная деформация пружины. Сила упругости пружины, как видно из (14.56), также является потенциальной силой.
Лю.
Работа вращающего момента
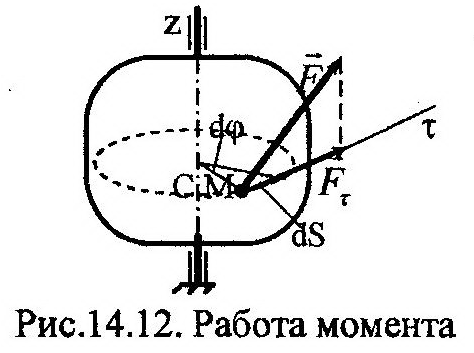
Определим работу вращающего момента MZ(F), создаваемого силой F, показанной на рис. 14.12. Элементарная работа этой силы будет равна:
В случае, если к телу приложена система сил, то выражение (14.65) можно записать в виде:
Работа вращающего момента на конечном угловом перемещении тела будет равен:
где φо, φ1 – начальная и конечная угловые координаты тела.
Кинетическая энергия точки
Если к каждой точке механической системы в любой момент времени, кроме фактически действующих на нее внешних и внутренних сил, приложить соответствующую силу инерции, то вся система сил будет приведена в равновесное состояние и к ней можно будет применять все уравнения статики. Следует иметь в виду: - принцип Даламбера можно применять для динамических процессов, протекающих в инерциальных системах отсчета. Этого же требования, как отмечалось ранее, следует придерживаться и при применении законов динамики; - силы инерции, которые, согласно методики принципа Даламбера, необходимо прило- жить к точкам системы, на самом деле на них не действуют. Действительно, если бы они существовали, то вся совокупность сил, приложенных к каждой точке, находилась бы в равновесии, и отсутствовала бы сама постановка задачи динамики. Для равновесной системы сил можно записать следующие уравнения:
т.е. геометрическая сумма всех сил системы, включая и силы инерции, и геометрическая сумма моментов всех сил относительно произвольного центра равны нулю. Учитывая свойства внутренних сил системы:
выражения (15.7) можно заметно упростить. Вводя обозначения главного вектора
и главного момента
выражения (15.7) предстанут в виде:
Уравнения (15.11) являются прямым продолжением принципа Даламбера, но не содержат внутренних сил, что является их несомненным преимуществом. Их использование наиболее эффективно при исследовании динамики механических систем, состоящих из твердых тел. ЛЕКЦИЯ 16. Принцип Лагранжа
Если принцип Даламбера позволяет привести систему в равновесное состояние, то принцип Лагранжа (принцип возможных перемещений) устанавливает в самом общем виде состояние равновесия. Таким образом, объектами его рассмотрения являются уравновешенные системы. Базовым понятием данного принципа является виртуальное (возможное) перемещение – это такое воображаемое достаточно малое Можных перемещений. Например, для свободной точки можно указать три независимых возможных перемещения (все три – линейные), а для свободного тела – шесть (три – линейные и три –
Введем понятие идеальной связи, реакция которой нормальна возможному перемеще-
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.126.74 (0.256 с.) |










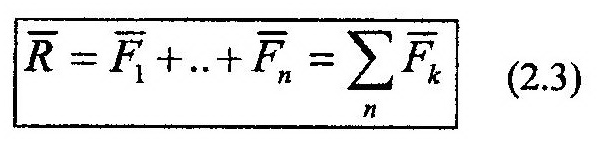













 Составляющие скорости точки по осям равны:
Составляющие скорости точки по осям равны:





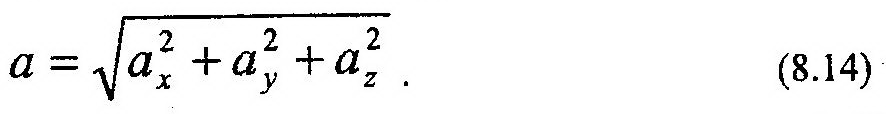


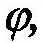

 Основными кинематическими характеристиками вращательного движения тела являются его: угловая скорость – величина, характеризующая изменение угловой координаты
Основными кинематическими характеристиками вращательного движения тела являются его: угловая скорость – величина, характеризующая изменение угловой координаты
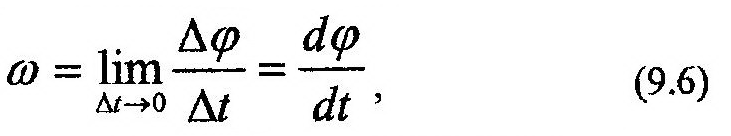 и угловое ускорение – величина, определяющая изменение угловой скорости
и угловое ускорение – величина, определяющая изменение угловой скорости












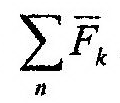


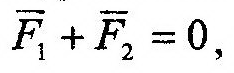
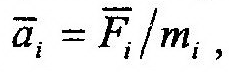







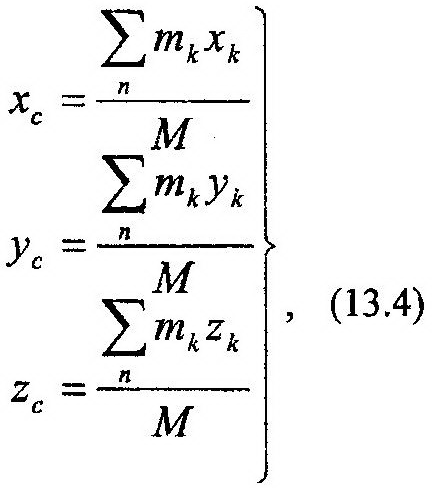


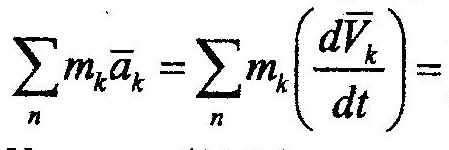







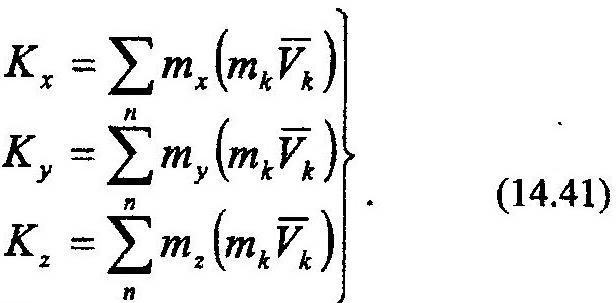

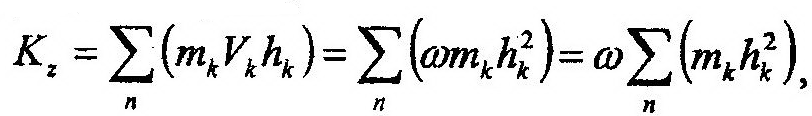 или Kz=Izω (14.43)
или Kz=Izω (14.43)



 или, учитывая, что Fτ=Fcosα, получим:
или, учитывая, что Fτ=Fcosα, получим:
 где dS – бесконечно малое перемещение точки М, показан-
ное на рис. 14.7.
Учитывая неоднозначность косинуса, знак работы получит-
где dS – бесконечно малое перемещение точки М, показан-
ное на рис. 14.7.
Учитывая неоднозначность косинуса, знак работы получит-






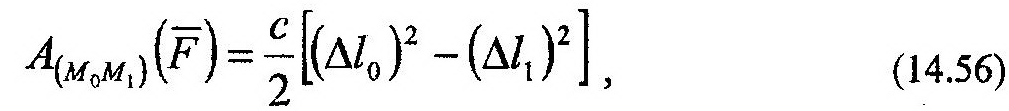
 где h=MC (см. рис. 14.12), а Fτh=Mz(F).
Тогда получим:
где h=MC (см. рис. 14.12), а Fτh=Mz(F).
Тогда получим:
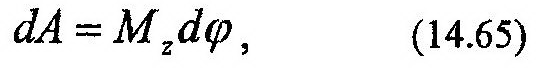 т.е.: элементарная работа вращающего момента силы
равна произведению его величины на элементарное приращение угловой координаты тела.
т.е.: элементарная работа вращающего момента силы
равна произведению его величины на элементарное приращение угловой координаты тела.


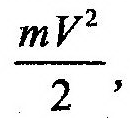





 где k1, k2 – скалярные коэффициенты.
где k1, k2 – скалярные коэффициенты.




