
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон распределения Пуассона
Если n велико, а p – мало, то хорошим приближением биномиального закона является закон Пуассона, который представляет собой закон распределения вероятностей массовых и редких событий. Дискретная случайная величина Х имеет закон распределения Пуассона, если она имеет бесконечное, но счетное множество возможных значений 0, 1, 2, …, k, … с вероятностями
где число Проверим, что сумма всех вероятностей равна единице:
Мы воспользовались разложением функции
Теорема. Если дискретная случайная величина Х распределена по закону Пуассона, то её числовые характеристики равны:
Доказательство. Докажем только первую формулу
С формулой Пуассона связан так называемый простейший поток событий. Поток событий – это последовательность однородных событий, которые наступают одно за другим в случайные моменты времени. Они часто встречаются в системах массового обслуживания (количество вызовов скорой помощи, такси и др.). Простейший поток событий – это поток событий со свойствами: 1) стационарность: вероятность того, что за время t произойдет k событий, т. е. 2) отсутствие последействия: предыстория потока не влияет на вероятность появления событий в будущем; 3) ординарность: появление двух и более событий за малый промежуток времени практически невозможно (например, поток поездов, подходящих к станции). Простейший поток характеризуется интенсивностью Обозначим
Геометрический закон распределения Дискретная случайная величина Х называется геометрически распределенной с параметром p, если она принимает значения
где
Примером такой случайной величины Х может быть число испытаний, проведенных до первого успеха, в схеме независимых повторных испытаний:
Проверим, что сумма всех вероятностей равна единице.
Мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии
Теорема. Если дискретная случайная величина Х распределена по геометрическому закону, то её числовые характеристики равны:
Показательный (экспоненциальный) закон распределения
Непрерывная случайная величина Х называется показательно-распределенной с параметром
Из определения плотности мы знаем, что Убедимся в том, что площадь, заключенная между графиком
Составим функцию распределения
Заметим, что с возрастанием x функция F(x) возрастает. Это означает, что если представить x как время, а F(x) – как вероятность отказа за время x некоторого устройства, то со временем эта вероятность в результате износа устройства постепенно растет. Таким образом, примером случайной величины, распределенной по показательному закону, может быть – время безотказной работы некоторого устройства.
Показательный закон играет большую роль в теории массового обслуживания и теории надежности. Например, случайная величина Х, равная интервалу времени между двумя соседними событиями в простейшем потоке, имеет показательное распределение с параметром Теорема. Числовые характеристики показательно распределенной непрерывной случайной величины вычисляются по формулам:
Доказательство. 1. Используя формулу интегрирования по частям
2. Для вычисления дисперсии найдем
По свойству 4 дисперсии имеем:
Тогда
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 823; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.12.205 (0.009 с.) |
 ,
,  ,
, – параметр закона Пуассона.
– параметр закона Пуассона.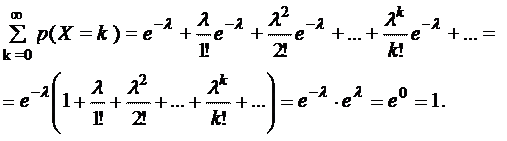
 в ряд Маклорена:
в ряд Маклорена:
 . (2.7)
. (2.7) .
.

 , зависит только от k и t и не зависит от начала и конца отсчета временного промежутка;
, зависит только от k и t и не зависит от начала и конца отсчета временного промежутка; (среднее число событий за единицу времени). Тогда
(среднее число событий за единицу времени). Тогда  – число событий за промежуток t.
– число событий за промежуток t. – вероятность появления k событий за промежуток времени t, тогда
– вероятность появления k событий за промежуток времени t, тогда .
. и вероятности этих значений вычисляются по формуле:
и вероятности этих значений вычисляются по формуле: ,
, ,
, 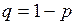 .
.

 , где
, где  .
.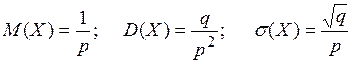 . (2.8)
. (2.8)
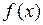 неотрицательна, следовательно, параметр
неотрицательна, следовательно, параметр  . График
. График 
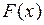 для показательного закона и построим её график (рис. 2.13).
для показательного закона и построим её график (рис. 2.13).




 . (2.9)
. (2.9) находим математическое ожидание:
находим математическое ожидание:


 , используя формулу интегрирования по частям:
, используя формулу интегрирования по частям: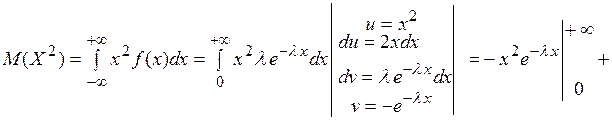

 .
. , что и требовалось доказать.
, что и требовалось доказать.


