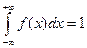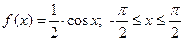Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достоверное событие и невозможное событие.Стр 1 из 3Следующая ⇒
Глава 1. Случайные события. §1. Предмет теории вероятностей. Теория вероятностей – это математическая наука, которая изучает закономерности массовых случайных явлений. Все явления реального мира могут быть закономерными и случайными. Закономерное событие – это событие, которое каждый раз осуществляется, как только создаются определённые условия. Случайное явление – такое явление, предсказать исход которого мы не можем. Пример. 1. Отказы технических устройств. Неизвестно, откажет или нет, когда откажет. 2. Промах при серии выстрелов по цели. Промах возникает от того, что не все факторы, от которых зависит данное явление, мы знаем и не все можем учесть. Если фактическое расстояние не совпадает с расчетным, то происходит промах. Форма пули, ствол, метеорологические условия отличаются от расчетных. Однако и в случайных явлениях можно заметить определённые закономерности при их многократном повторении. Пример. 1. Каждая молекула движется хаотично. Масса молекул ведет себя закономерно. 2. При стрельбе по мишени: Ограниченное число выстрелов – нет закономерности в расположении пробоев. Многократное повторение – пробои мишени заполняют эллипс. Чем больше стреляем, тем более отчетливо проявляется закономерность. 3. Проводится опыт, в результате которого может пpоявится событие А, n – количество всех опытов, nA – количество опытов, в результате которых проявилось событие А.
Чем больше количество опытов n, тем отчётливее проявляется закономерность проявления события. Т.е. при многократном проведении опытов частота проявления события стабилизируется около некоторой величины. Такое свойство, характерное для случайных опытов при их многократном проявлении, называется свойством устойчивости частот. Это свойство устойчивости частот при больших n наблюдается и для широкого круга случайных явлений. Случайные явления, которые можно, по крайней мере, принципиально наблюдать много раз, называются массовыми. Факт устойчивости частот, наблюдаемый в массовых случайных явлений, является основой построения теории вероятностей. Однако теория вероятностей имеет дело не со случайными явлениями реального мира, а занимается построением и изучением математических моделей случайных явлений и опытов. Методы теории вероятностей широко используются в различных отраслях науки и инженерной практики: теория надёжности, теория управления, теория стрельбы, теория массового обслуживания, астрономия. Она является теоретической основой для прикладной и математической статистики.
§2. Случайный опыт. Случайные события. Элементарные события.
Будем называть опытом каждое осуществление некоторого комплекса условий и действий, который каждый раз должен строго выполняться при повторении данного опыта. Если результаты опыта неоднозначно определяются условиями опыта и обладают свойством устойчивости частот при его многократном повторении, то такие опыты называются случайными опытами. Всякий факт, который показывает, обладает результат опыта каким-либо свойством или нет, называют случайным событием опыта. Элементарное событие. Элементарным событием случайного опыта будем называть такое событие, которое определяется следующими двумя условиями: 1. В результате опыта происходит одно и только одно элементарное событие e. 2. Каково бы ни было событие А, связанное с данным опытом, после осуществления элементарного события e можно дать однозначный ответ: наступило или нет событие. Любое случайное событие опыта есть некоторая совокупность элементарных событий случайного опыта, характеризуемая каким-либо определённым признаком. Пример. 1. Бросается игральная кость. e – цифра, наблюдаемая на верхней грани кубика. e1 =1, e2 =2, e3 =3, e4 =4, e5 =5, e6 =6. A – выпала четная цифра. А = {2, 4, 6} B – меньше пяти. B = {1, 2, 3, 4} Пример. В ящике 10 шаров, неразличимых на ощупь. Шары помечены номерами 1-10. Шары с номером 1-5 – красные; 6-9 – белые; 10 – синий. Доля шаров красного цвета - Производится опыт: вынимается шар и записывается результат наблюдения: номер шара, его цвет. Затем шар возвращается в ящик и шары в нём перемешиваются. Экспериментатор не знает количество шаров и долю шаров каждого цвета. Поставлена задача: сколь угодно раз повторяя опыт определить количество шаров в ящике и доли шаров каждого цвета.
Пусть опыт провели n раз и результаты опыта занесли в таблицу:
Элементарное событие - # шара (1-10). Событие А – красный шар (1,2,3,4,5) Событие В – шар белого цвета (6,7,8,9) Событие С – синий шар (10) Результаты опытов зависят от числа проведённых опытов, т.к. при повторении опытов могут появиться шары с новыми номерами и нового цвета. При увеличении числа опытов n результаты опытов всё меньше и меньше будут пополняться новыми данными о номерах шаров и их цвете, т.е. новыми данными об элементарных событиях и событиях опыта А, В, С. Частоты событий А, В, С будут колебаться незначительно, стабилизируясь около чисел Анализ результатов опыта позволяет ввести математическую модель опыта. Для этого нужно: 1. Задать множество элементарных событий случайного опыта (1, 2, …,10). 2. Составить из данных элементарных событий события случайного опыта А, В, С. 3. Задать на событиях числовую характеристику возможности их появления – вероятности событий. Основанием для введения вероятностей является свойство устойчивости частот.
§3. Пространство элементарных событий.
Для построения математической модели случайного опыта, прежде всего, введём пространство элементарных событий. Множество всех возможных элементарных событий случайного опыта будем называть пространством элементарных событий, связанных с данным случайным опытом Е. В процессе изучения математической модели случайного опыта будем рассматривать только элементы этого множества и его различные подмножества. Пространство элементарных событий называется дискретным, если оно содержит конечное или счётное число элементарных событий. Обозначение для конечного пространства - Е ={ e1, e2,…, en } E = { e1, e2, …, en,…} Любое подмножество А дискретного пространства элементарных событий Е называется событием модели. Говорят, что событие А составлено из элементарных событий или содержит элементарные события. Пример. 1. Бросание кости. E ={ e1, e2, e3, e4, e5, e6 } Любое подмножество этого множества является событием модели. 2. В городе эпидемия гриппа. Случайным образом из населения города отобрали 50 человек, выяснили, сколько из них из них больны гриппом. А – больные гриппом Е – число больных Е ={0, 1, …, 50} A ={0, 1, …,24} В теории вероятностей в качестве пространства элементарных событий используется множество всех точек некоторого промежутка числовой прямой, либо в области на плоскости или области в пространстве. В этом случае пространство элементарных событий называется непрерывным. В случае непрерывного пространства Е под событием понимается не любое подмножество пространства Е, а некоторое подмножество, обладающее определённым свойством. Пример. 1. На плоскость квадрата случайным образом бросается точка. е – точка квадрата, в которой упала брошенная точка. Е – множество всех точек квадрата. Под событием понимается подмножество е, имеющее площадь.
§4. Соотношение между событиями. Действия над событиями.
Задано пространство событий Е А, В, С – события Противоположное событие. Событие
Событие Пример.
2)
Несовместные события. Событие А и событие В называются несовместными, если их пересечение есть несовместное событие:
Пример: Бросается игральный кубик. Рассмотрим события: А1 – число очков делится на 3 А2 – число очков делится на 5 А3 – число очков делится на 2 Не являются группой попарно несовместных событий, т.к. Полная группа событий. Говорят, что события 1) Они попарно несовместны: 2) Их объединение – есть событие достоверное:
Опыт: 2 выстрела по мишени А1 – хотя бы одно попадание А2 - хотя бы один промах е – количество дырок в мишени
Опыт: бросание двух монет А1 – появление двух гербов А2 – появление двух цифр е – появление герба или цифры
§5. Аксиомы теории вероятностей.
Поле событий. Пусть введено некоторое пространство элементарных событий Е, некоторое подмножество А из Е мы называем событием. Среди множества всех подмножеств пространства Е выделим такой класс К подмножеств пространства, который обладает следующими свойствами: 1) класс К в качестве элементов содержит достоверное и невозможное событие: 2) если 3) если события Такой класс К подмножеств пространства Е называется аддитивным классом. Аддитивный класс К подмножеств А из Е мы будем называть полем событий. Пример. 1) опыт: бросается игральный кубик
В этом случае под событием мы понимаем любое подмножество пространства Е. Поэтому поле событий К в случае дискретного пространства Е есть множество всех подмножеств пространства Е.
Все эти события составляют поле событий. 1. 2. 3. 2) точка случайным образом брошена на отрезок [0;1] и наблюдается 2 события: А1 – попадание точки в промежуток [0;½) A2 – попадание точки в промежуток [½;1]
Под событием понимаем то, что имеет длину. 1. 2.
3.
Аксиомы. Пусть задано пространство элементарных событий Е и поле событий К на этом пространстве. Числовая функция Р (А),
1) 2) вероятность достоверного события является единицей, Р (Е)=1 3) аксиома сложения вероятностей: если Вероятностное пространство. Говорят, что имеется вероятностная (математическая) модель случайного опыта, если построены: 1) пространство элементарных событий Е 2) поле событий К 3) распределение вероятностей на поле событий К, т.е. для каждого события А из поля событий К задана вероятность Р (А) Тройка объектов (Е, К, Р) называется вероятностным пространством (моделью) данного случайного опыта. Если Е – дискретное, то (Е, К, Р) называется дискретным. Если Е – непрерывное, то (Е, К, Р) называется непрерывным.
§6. Классическая вероятностная модель.
Вероятностная модель называется классической, если выполнены следующие 2 условия: 1) пространство элементарных событий – дискретное конечное, состоит из n элементарных событий Е ={ e1, e2, …, en } 2)
Вероятностное пространство определяется так: для заданного пространства Е поле событий К - есть множество всех подмножеств из Е, а вероятности Р (А) для любого события А из К выражаются через вероятности элементарных событий. Пусть По аксиоме 3:
§7. Геометрические вероятности.
Классическая модель: дискретная вероятностная модель Геометрическая модель: непрерывная вероятностная модель (Е, К, Р) Е – непрерывное пространство, множество точек области на плоскости К ={ A } А из Е: А – длина; А – площадь; А – объём
Наудачу бросается точка, наблюдается событие: попадание точки в область А. «Наудачу» означает: вероятность события А зависит от площади А, не зависит от её формы и положения Е.
§8. Теорема о сложении вероятностей.
(Не путать с аксиомой о сложении вероятностей). Теорема. Задано вероятностное пространство (Е, К, Р), есть события А, В
По аксиоме 3:
Вычитая из 1-го равенства 2-е получим ч.т.д. Замечание: из аксиомы 3 следует, что если события
§9. Условные вероятности.
Пример. Три раза бросается монета. Результат: цифра или герб.
n =8 A – герб выпал один раз;
Пусть в результате опыта произошло событие В. Число выпавших гербов – нечётно.
Тогда, если В произошло, Рассмотрим более общую ситуацию: пусть некоторому случайному опыту соответствует классическая вероятностная модель.
r элементарных событий входит и в А и в В. Найдём вероятность события А при условии, что произошло В. Если В произошло, то его вероятность равна 1, то Событие А происходит, если происходит элементарное событие, принадлежащее пересечению, их всего r.
Определение: пусть задано вероятностное пространство (Е, К, Р); А, В – события. Если Формула полной вероятности. Пусть (Е, К, Р) – модель некоторого случайного опыта. Н1, Н2, …, Нn – полная группа. 1) 2)
Hi – гипотеза
Доказательство: т.к. Hi – попарно несовместные, Пример. Имеются 3 одинаковых урны. Состав: 1-я – 2 белых, 1 чёрный; 2-я – 3 белых, 1 чёрный; 3-я – 2 белых, 2 чёрных. Наудачу выбирается урна; из неё вынимается шар. Найти вероятность того, что шар – белый. Гипотезы: Hi – выбрана i -я урна, i =1,2,3.
А – шар белый
Формулы Байеса. Если вероятности гипотез до опыта известны, то их называют априорные вероятности гипотез. Пусть известно, что событие А произошло. Вероятность всех гипотез изменяется. Вероятности гипотез после того, как событие А произошло – апостериорные вероятности. Пусть в условиях предыдущего примера известно, что вытащен белый шар. Найти вероятность того, что шар вытащен из второй урны.
§11. Последовательности независимых испытаний. Схема Бернулли.
До сих пор мы рассматривали один опыт, для него строили вероятностную модель (Е, К, Р). Теперь будем рассматривать несколько опытов, причём каждый имеет 2 исхода ( Будем рассматривать составной опыт, составленный из таких n независимых опытов. Вероятностная модель такого составного опыта называется схемой Бернулли. Построим вероятностное пространство составного опыта. (Е, К, Р) 1. E, e – результат совместного (одновременного) рассмотрения исходов n испытаний (опытов). Элементарные события будем записывать в виде последовательности букв У и Н. е =(УННУ … У) (*) Причём, если в опыте с номером k имел место успех, то на k -м месте ставим У, неудача – Н.
Е – множество всех конечных последовательностей вида (*). Е – конечное
2. K ={ A } 3.
Если m раз – успех
Всего таких е, которые составляют событие А – это число способов расставить букву У на m местах среди n мест, т.е. это число сочетаний из m по n (
Вероятность того, что расход электроэнергии в течение суток не превысит установленной нормы – 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит установленной нормы. У – расход нормы не превысит нормы Н – норма будет превышена Р (У)=0,75; Р (Н)=0,25 n =6
Случайная величина. Случайная величина и числовая функция элементарного события – это не одно и то же. Мало задать числовую функцию, надо знать вероятности множества значений, которые может принимать эта функция. Определение. Случайной величиной называется числовая функция элементарного события е, определённая на пространстве элементарных событий Е такая, что для любого
Рассмотрим
§2. Функция распределения случайной величины и её свойства.
Определение. Функцию
Эту функцию называют функцией распределения случайной величины Х. Свойства функции распределения случайной величины: 1. 2. Доказательство.
3. F (x) – неубывающая функция,
По свойству 2 4. Если функция F (x) непрерывна при x = x1, то P { X = x1 }=0. Функция y = f (x) непрерывна при x = x1, если Дадим Δx, подсчитаем ΔF: При 5. Укажем без доказательства следующее свойство: 6. 7. F (x) – непрерывна слева:
§3. Дискретные случайные величины.
Случайные величины различны по природе. Нужные в практике удовлетворяют случайные величины дискретные и непрерывные. Случайная величина называется дискретной, если множество её возможных значений является конечным или счётным.
Дискретная случайная величина полностью определена, если заданы вероятности этих возможных значений.
Обычно дискретную случайную величину (закон распределения случайной величины) задают таблицей.
Таблица 1
Эту таблицу называют рядом распределения случайной величины. Пример. Бросаются две игральные кости: зелёная и красная. Рассматривается случайная величина х – сумма выпавших очков на двух костях. Составить закон распределения этой случайной величины.
X = i + j
Закон распределения может быть задан функцией распределения дискретной случайной величины. Дискретная случайная величина задана:
Найти функцию распределения и построить её график.
График распределения имеет ступенчатый вид. Скачки происходят в точках, соответствующих возможным значениям и скачки равны вероятности этих значений.
Примеры дискретных распределений случайной величины: 1. В схеме Бернулли с n испытаниями рассмотрим случайную величину X (e)= m – суммарное число успехов за n испытаний. 0, 1, 2, …, n – возможные значения случайной величины.
Распределение X (e) суммарного числа успехов в схеме Бернулли называется биномиальным распределением. Биномиальный ряд распределения случайной величины:
Пример. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте – 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Случайная величина Х – число отказавших элементов в одном опыте. У – отказ; Р (У)=0,1; q =0,9
Закон Пуассона. Закон приближения биномиального распределения в случае, когда р – весьма мала, n – весьма велико.
Пусть
(1) Распределение дискретной случайной величины согласно (1) называется распределением Пуассона. Это распределение зависит только от а. Пример. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится – 0,0002. найти вероятность того, что на базу прибудут 3 негодных изделия. p =0,0002; k =3; n =5000
§4. Непрерывные случайные величины.
Под непрерывной случайной величиной понимают случайную величину, возможные значения которой сплошь заполняют некоторый промежуток. Определение 1. Пусть F (x) – функция распределения случайной величины Х, F (x) – дифференцируема: Случайная величина Определение 2. Функция
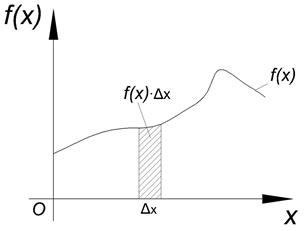
В числителе вероятность того, что случайная величина принимает значение в интервале длиной Δх. Отношение под знаком lim задаёт вероятность, приходящуюся на единицу длины. Беря предел, получим плотность вероятностей. График функции f (x) называется кривой распределения. Заметим, что f (x) существует только для непрерывной случайной величины. Из (*) Отбрасывая бесконечно малую более высокого порядка, получаем приближённое значение.
Из (1) Теорема. Вероятность того, что непрерывная случайная величина принимает значение в интервале от α до β Доказательство.
F (x) – первообразная для f (x)
По формуле Ньютона-Лейбница
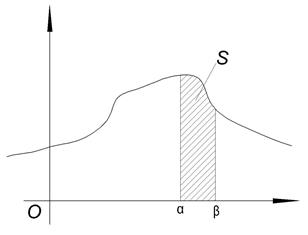
Геометрически:
Свойства f ( x ): 1°. Доказательство: 2°.
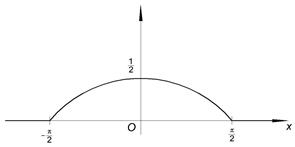
Геометрически 1° и 2° означают, что график функции f (x) расположен выше либо на оси ОХ и площадь под кривой f (x)=1. Пример. Задана функция 1) определить а; 2) построить график f (x); 3) определить F (x) и график; 4) 1) Найдём а:
2)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.86 (0.308 с.) |
 – частота проявления события А в n опытах.
– частота проявления события А в n опытах. , 6-9 -
, 6-9 -  , 10 -
, 10 -  .
. большинство здоровых
большинство здоровых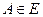 - не является событием.
- не является событием.
 называется противоположным событию А, если оно состоит в том, что не наступает событие А.
называется противоположным событию А, если оно состоит в том, что не наступает событие А. 1)
1)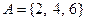
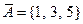
 ,
, 

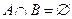
 и
и 
 составляют группу попарно несовместных событий, если
составляют группу попарно несовместных событий, если 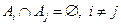 .
.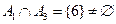


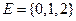

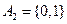
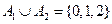

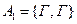


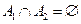


 (в конечном или счётном числе) принадлежат классу К, то их объединение или пересечение в конечном или счётном числе также принадлежит классу К.
(в конечном или счётном числе) принадлежат классу К, то их объединение или пересечение в конечном или счётном числе также принадлежит классу К. - дискретное пространство элементарных событий.
- дискретное пространство элементарных событий.
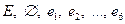



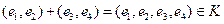

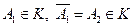

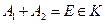

 называется вероятностью, если выполнены следующие аксиомы:
называется вероятностью, если выполнены следующие аксиомы: ставится в соответствие неотрицательное число
ставится в соответствие неотрицательное число 
 )
)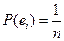 - вероятности всех элементарных событий равны
- вероятности всех элементарных событий равны


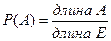 ;
; ;
; .
. Эти вероятностные пространства служат моделью задач такого типа:
Эти вероятностные пространства служат моделью задач такого типа: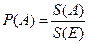
 Е.
Е.
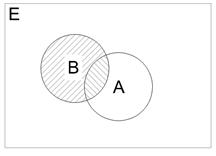






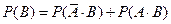




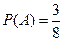

 .
. , n элементарных событий
, n элементарных событий

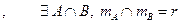
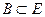

 .
.
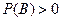 , то условной вероятностью события А при условии, что событие В произошло, называется отношение
, то условной вероятностью события А при условии, что событие В произошло, называется отношение 




 , по аксиоме 3
, по аксиоме 3  .
.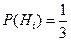 .
.
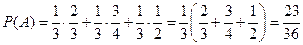 .
.

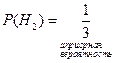
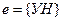 (успех, неудача).
(успех, неудача).  ;
;  .
.
 - означающее, что в составном опыте m из n раз имел место успех.
- означающее, что в составном опыте m из n раз имел место успех.
 ).
). - формула Бернулли.
- формула Бернулли.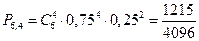
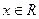 определены вероятности событий
определены вероятности событий 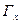 , где
, где  .
. . Числовая функция
. Числовая функция 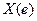 осуществляет отображение пространства Е на числовую ось.
осуществляет отображение пространства Е на числовую ось.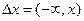
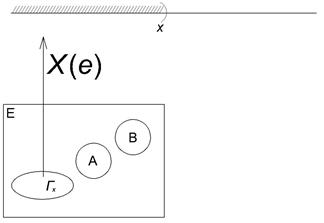 Требуется, чтобы
Требуется, чтобы  . В противном случае это не будет событием.
. В противном случае это не будет событием.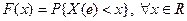 называют функцией распределения.
называют функцией распределения.
 в соответствии с аксиомой 1 и 2.
в соответствии с аксиомой 1 и 2.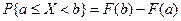
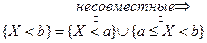

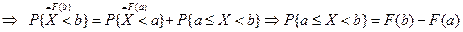 .
.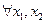 -
- 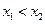

 .
. .
.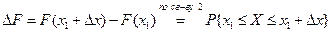
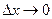 получим
получим 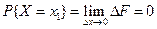 , т.к. F (x) непрерывна при x = x1.
, т.к. F (x) непрерывна при x = x1.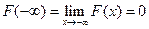 .
.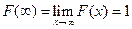 .
.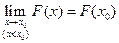 .
.
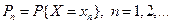 , Pn ≥0
, Pn ≥0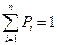

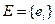 ,
, 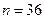 ,
, 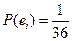
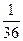
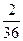
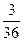


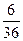




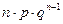
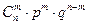

 ;
;  ;
; 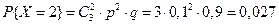 ;
; 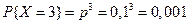 .
.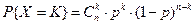 (*)
(*)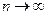 ,
, 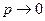 , но
, но 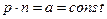 .
.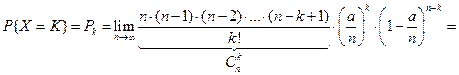
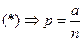


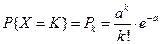 ,
,  .
.
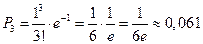 .
.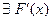 .
. неотрицательная функция f (x), интегрируемая на всей числовой оси и такая, что
неотрицательная функция f (x), интегрируемая на всей числовой оси и такая, что 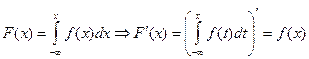 .
.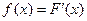 называется плотностью распределения и плотностью вероятностей непрерывной случайной величины.
называется плотностью распределения и плотностью вероятностей непрерывной случайной величины.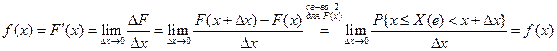 (*)
(*)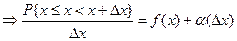 ;
; 
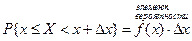
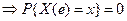 .
.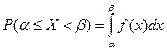 .
.
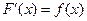
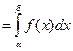 .
.

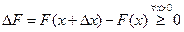 , т.к. по свойству 3 F (x) – неубывающая. Тогда
, т.к. по свойству 3 F (x) – неубывающая. Тогда  .
.

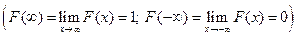
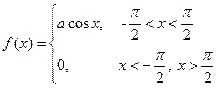
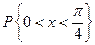 .
.