
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторные независимые испытания
В этой теме рассматривается ситуация, когда некоторое испытание производится несколько раз: например, подбрасывается монета, или производятся выстрелы по мишени, и т.д. Один исход испытания выделен и назван успехом. В этой схеме, называемой схемой Бернулли, выделяются следующие параметры: n – число испытаний; p – вероятность успеха в одном испытании; q = 1 – p – вероятность неуспеха в одном испытании. Число успехов в п испытаниях может принимать значения от 0 до п. Это число обозначим µ n. Нас интересует вероятность того, что µ n примет заданное значение m, то есть Р (µ n = m). Эту вероятность можно обозначить Рn (m). Теорема 1.8.1 (формула Бернулли). Рn (m) = Пример 1. Какова вероятность, что при 5 бросаниях игральной кости ровно 2 раза выпадет 6 очков? Решение. В схеме Бернулли имеем параметры: п = 5; р = 1/6; q = 5/6. По формуле Бернулли получаем Р 5(2) = Теорема 1.8.2. Наиболее вероятное число успехов в схеме Бернулли m 0 удовлетворяет неравенству np – q £ m 0£ np + p. Разность между границами этого неравенства равна 1, значит, в указанном промежутке обязательно есть целое число. Это число и есть искомое наиболее вероятное число успехов. При этом возможно, что целочисленными являются границы промежутка. В этом случае они являются двумя значениями наиболее вероятного числа успехов, соответствующие вероятности будут одинаковы. Пример 2. Какое наиболее вероятное число выпадений 6 очков а) при 20; б) при 17 бросаниях игральной кости? Решение. Воспользуемся теоремой 1.8.2: а)
m 20= 3. б) 2 £ m 0£ 3; m 0= 2 или m 0= 3. При больших значениях п вычисления по формуле Бернулли становятся слишком громоздкими. В этом случае используются приближенные формулы. Теорема 1.8.3 (локальная теорема Муавра – Лапласа). В схеме Бернулли при большом числе испытаний п имеет место приближенная формула Рn (m) = Эта формула дает хороший результат при п ³ 30, при этом р должно быть не слишком близко к 0 или 1. Здесь функция j(х) – это функция Гаусса, или плотность вероятностей. Она имеет вид j(х) =
Пример 3. Какова вероятность, что при 100 бросаниях игральной кости ровно 20 раз выпадет 6 очков? Решение. В схеме Бернулли имеем параметры: п = 100; р = 1/6; q = 5/6. По локальной теореме Муавра – Лапласа вычисляем:
Р 100(20) = Бывают ситуации, когда требуется вычислить вероятность того, что число успехов в схеме Бернулли принадлежит некоторому промежутку: a £ µ n £ b. В этом случае можно отдельно посчитать и сложить вероятности для µ n = a, a + 1, …, b. Но объем вычислений будет большой, и для таких случаев также используется приближенная формула. Теорема 1.8.4 (интегральная теорема Муавра – Лапласа). В схеме Бернулли при большом числе испытаний п имеет место приближенная формула Рn (a £ µ n < b) = Область применения интегральной теоремы Муавра – Лапласа та же, что для локальной теоремы Муавра – Лапласа. Здесь используется функция Ф(х) = называемая интеграл вероятностей, ее таблица также приводится в книгах. Эта функция нечетная, то есть при наличии у аргумента знака «–» этот минус выносится за знак функции. Таблица значений этой функции обычно приводится только для х £ 4, при x > 4 значение Ф(х) можно считать равным 0,5. Следует иметь в виду, что в разных источниках функция Ф(х) определяется несколько по-разному, и это влияет на вид формулы в интегральной теореме Муавра – Лапласа. Таблица применима для приведенной выше формулы, если значения функции в конце таблицы приближаются к 0,5. Пример 4. Какова вероятность, что при 100 бросаниях игральной кости 6 очков выпадет: а) от 15 до 20 раз; б) не менее 20 раз? Решение. Воспользуемся решением примера 3: п = 100; р = 1/6; q = 5/6, а) Р (15£ µ n £ 20) = Р (15£ µ n < 21) = б) Р (µ n ³ 20) = Р (20£ µ n < 100) = = Ф(22,3) – Ф(0,89) = 0,5 – 0,3113 = 0,1887. Упражнения 8.1. Какова вероятность, что в серии из 5 выстрелов будет: а) ровно 1 попадание; б) не менее одного попадания, если вероятность попадания при одном выстреле равна 0,3?
8.2. Всхожесть семян равна 0,8. Какова вероятность, что из 5 посеянных взойдут ровно 4? 8.3. Всхожесть семян равна 0,8. Какое наиболее вероятное число взошедших семян из 10 посеянных? Найдите соответствующую вероятность. 8.4. Какова вероятность, что при 5 бросаниях игральной кости ровно один раз выпадет 6 очков? 8.5. В институте девушки составляют 70% от числа студентов. Какова вероятность, что среди первых пяти встретившихся студентов а) ровно три девушки; б) хотя бы один юноша; в) хотя бы одна девушка? 8.6. Вероятность попадания в мишень 0,7. Найдите наиболее вероятное число попаданий при 40 выстрелах. Какова вероятность, что будет: а) ровно 30 попаданий; б) от 25 до 30 попаданий; в) не более 30 попаданий? Случайные величины В предыдущих темах математической обработке подвергались только вероятности событий. Важной представляется ситуация, когда сами события имеют математический смысл: например, когда указывается число выпавших очков при подбрасывании игрального кубика, или число успехов в схеме Бернулли. В этих случаях испытание заключается в случайном выборе некоторого числа. Задается некоторое числовое множество, из которого производится выбор, и выбираемой число является переменной величиной, принимающей случайные значения. Эта переменная называется случайной величиной. Среди случайных величин выделяются дискретные и непрерывные. Дискретныемогут принимать либо конечное число значений, либо бесконечное, но значения отделены друг от друга числовыми промежутками (в этом смысл термина дискретность). Непрерывная случайная величинапринимает значения из некоторого числового промежутка. Например, непрерывной случайной величиной является отклонение размера изготовленной детали от расчетного значения. Задать закон распределения случайной величины– это значит описать ее поведение. Закон распределения несет информацию о значениях случайной величины и вероятностях, с которыми эти значения принимаются. Конечную дискретную случайную величину Х можно задать с помощью таблицы, в которой указываются значения случайной величины и вероятности, с которыми эти значения принимаются. Такая таблица имеет вид
Обязательное условие: сумма вероятностей во второй строке равна 1. Такая таблица называется ряд распределения. Случайная величина может быть задана также с помощью формулы. Например, число успехов в п испытаниях в схеме Бернулли – это случайная величина, принимающая значения от 0 до п. Соответствующие вероятности определяются формулой Бернулли. Константу также можно рассматривать как случайную величину, принимающую единственное значение с вероятностью 1. Способы задания непрерывной случайной величины будут описаны ниже. Две случайных величины Х и Y являются независимыми, если для любого множества значений А случайной величины Х и любого множества значений В случайной величины Y независимыми являются события: «значение Х принадлежит множеству А» и «значение Y принадлежит множеству B». По определению независимых событий это означает, что вероятность произведения этих событий равна произведению их вероятностей. В частности, это относится к случаю, когда А и В состоят из одного значения.
Над случайными величинами определены следующие операции. Умножение на число. При умножении случайной величины Х на число с все значения Х умножаются на с, а вероятности остаются прежними. Сложение случайных величин. При выполнении этой операции все значения случайных величин попарно складываются. Для независимых случайных величин вероятность каждого получившегося суммарного значения равна произведению соответствующих вероятностей. При выполнении операции могут получаться одинаковые суммы, тогда эти суммы нужно объединить в одно значение, сложив соответствующие вероятности. Для зависимых случайных величин вероятность для любой суммы определяется характером зависимости. Умножение случайных величин. При выполнении этой операции все значения случайных величин попарно перемножаются. Вероятности определяются так же, как при сложении. Возведение случайной величины Х в степень. Все значения случайной величины Х возводятся в эту степень, вероятности остаются прежними. При появлении одинаковых значений они объединяются в одно, соответствующие вероятности складываются. Аналогично можно вычислять другие функции от случайных величин. Пример 1. Заданы ряды распределения независимых случайных величин Х и Y.
Постройте ряды распределения для 2 Х, X+Y, XY, X 2. Решение. Для 2 Х результат получается сразу:
Для X+Y сначала находим попарные суммы, перемножая соответствующие вероятности:
Замечаем, что среди получившихся значений суммы оказалось два одинаковых, равных 3. Объединяем их, сложив соответствующие вероятности. Значения переставляем, располагая их в порядке возрастания:
Аналогично находим произведение случайных величин:
После объединения одинаковых значений и упорядочивания получаем
При нахождении Х 2 также происходит объединение значений и упорядочивание:
Поведение случайной величины характеризуется различными параметрами. Один из основных – это математическое ожидание, смысл которого – среднее значение случайной величины. Но это не среднее арифметическое, а среднее значение с учетом вероятностей, с которыми принимаются значения случайной величины.
Для дискретной случайной величины Х математическое ожиданиевычисляется по формуле MX = x 1 p 1 + … + xnpn = Теорема 1.9.1. Свойства математического ожидания. 1*. М (С) = С, где С – константа. 2*. М (СХ) = С МХ, где С – константа. 3*. М (X + Y) = MX + MY. 4*. М (XY) = MX . MY, если Х и Y независимы. Другая характеристика случайной величины – это дисперсия, характеризующая разброс значений случайной величины относительно среднего значения. Она вычисляется по формуле DX = M ((X – MX)2) (2) Смысл этой формулы следующий. Сначала берем отклонения случайной величины Х от ее математического ожидания, то есть случайную величину Х – МХ. Отклонения могут иметь положительный или отрицательный знак. Нас интересует среднее значение отклонения без учета знака, то есть модуля отклонения. Но модуль – это функция, неудобная для математической обработки, так как производная от нее является разрывной функцией. Поэтому вместо модуля, чтобы убрать знак, берут квадрат разности и ищут его среднее значение. Теорема 1.9.2. Свойства дисперсии. 1*. DС = 0, где С – константа. 2*. D (СХ) = С 2 МХ, где С – константа. 3*. D (X + Y) = DX + DY,если Х и Y независимы. 4*. DX = M (X 2) – (MX)2. Последняя формула обычно используется вместо определения для практического вычисления дисперсии. Если случайная величина получена в результате физических измерений и имеет размерность (масса в кг, длина в м, время в с и т.д.), то дисперсия будет иметь квадратную размерность. Поэтому дисперсия не дает среднее значение разброса, а только позволяет его оценить. Среднее значение разброса показывает среднее квадратичное отклонение, вычисляемое по формуле
Пример 2. Задан ряд распределения случайной величины Х.
Найдите МХ, DX, σ(X). Решение. МХ = 0 . 0,3 + 1 . 0,2 + 3 . 0,1 + 5 . 0,4 = 2,6; M (X 2) = 02 . 0,3 + 12 . 0,2 + 32 . 0,1 + 52 . 0,4 = 11,1; DX = M (X 2) – M (X)2 = 11,1 – 2,62 = 4,34;
Упражнения 9.1. Задан ряд распределения случайной величины Х:
Найдите МХ, DX, σ(X). 9.2. Производятся три выстрела по мишени с вероятностью попадания при одном выстреле 0,6. Число попаданий является случайной величиной. Постройте ряд распределения для этой случайной величины. 9.3. В урне 5 белых и 4 черных шара. Наугад вынимаются два шара. Постройте ряд распределения для случайной величины – числа вынутых белых шаров. Найдите ее математическое ожидание, дисперсию и среднее квадратичное отклонение.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.165.246 (0.037 с.) |
 .
. =
=  =
=  = 0,16.
= 0,16. £ m 0£
£ m 0£  ;
;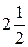 £ m 0£
£ m 0£  ;
; £ m 0£
£ m 0£  ;
; .
.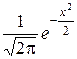 . В практических вычислениях используется таблица значений этой функции, которая приводится практически во всех справочниках и учебниках по теории вероятностей. Эта функция четная, значит, при отрицательных значениях аргумента знак «–» отбрасывается. В таблицах для j(х) обычно приводятся значения только для х £ 4, при x > 4 значение j(х) можно считать равным 0.
. В практических вычислениях используется таблица значений этой функции, которая приводится практически во всех справочниках и учебниках по теории вероятностей. Эта функция четная, значит, при отрицательных значениях аргумента знак «–» отбрасывается. В таблицах для j(х) обычно приводятся значения только для х £ 4, при x > 4 значение j(х) можно считать равным 0.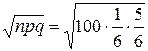 = 3,73;
= 3,73; =
=  =
=  = 0,072.
= 0,072.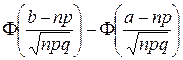 .
.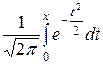 ,
, = 3,73. По интегральной теореме Муавра – Лапласа получаем:
= 3,73. По интегральной теореме Муавра – Лапласа получаем: = Ф(1,16) – Ф(–0,45) = 0,3370 + 0,1736 = 0,5106.
= Ф(1,16) – Ф(–0,45) = 0,3370 + 0,1736 = 0,5106. =
= (1)
(1) (3)
(3) = 2,08.
= 2,08.


