
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование временных рядов: оценка адекватности уравнений тренда ⇐ ПредыдущаяСтр 5 из 5
Цель: провести корреляционный анализ данных и спецификацию модели; проанализировать тесноту связи между показателями на проблему мультиколлинеарности факторов; оценить параметры регрессии и качество модели; проанализировать значимость результатов регрессионного моделирования, влияние факторов на зависимую переменную; выполнить точечное и интервальное прогнозирование с помощью полученной модели; провести регрессионный анализ выбранной модели с помощью ППП MS Excel.
Теоретические сведения математическим аппаратом, используемым для решения задач анализа временных моделей, являются методы корреляционно – регрессионного анализа. Связь между объясняемой переменной Y (t) и m независимыми факторами можно представить в виде функции регрессии: Y (t) = f (х 1, х 2,..., хт), которая показывает, каково будет в среднем значение переменной Y, если переменные х примут конкретные значения. Регрессионные модели используются не только для анализа, но и для прогнозирования экономических явлений. В качестве зависимой переменной может выступать практически любой показатель, характеризующий, например, деятельность коммерческого банка или означающий курс ценной бумаги. Основными этапами построения регрессионной модели являются: · построение системы показателей (факторов). Сбор и предварительный анализ исходных данных; · построение и анализ матрицы коэффициентов парной корреляции; · выбор вида модели и численная оценка ее параметров; · проверка качества модели; · оценка влияния отдельных факторов на результативный признак с помощью построенной модели; · прогнозирование на основе модели регрессии. Выбор факторов, влияющих на исследуемый показатель, производится, прежде всего, исходя из содержательного анализа социально–экономических явлений с использованием статистических и математических критериев. Для получения надежных оценок в модель не следует включать слишком много факторов. Их число не должно превышать одной трети объема имеющихся данных (т £ п /3). Для определения наиболее существенных факторов могут быть использованы коэффициенты линейной и множественной корреляции (детерминации), частные коэффициенты корреляции. На основании содержательного анализа составляется перечень показателей, которые предполагается включить в модель. Затем производится сбор статистической информации и предварительный анализ данных.
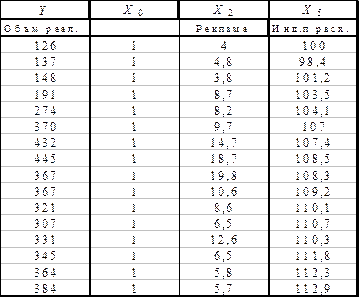
Значения переменных Y и X, содержащиеся в наблюдаемой совокупности, записываются в таблицу исходных данных (табл. 14). Таблица 14
Далее производятся сравнительная оценка и отсев части факторов путем анализа парных коэффициентов корреляции
Чем ближе значение коэффициента корреляции к 1, тем теснее связь. Связь считается достаточно сильной, если коэффициент корреляции по абсолютной величине превышает 0,7, и слабой, если он меньше 0,4. При равенстве коэффициента корреляции нулю связь полностью отсутствует. Коэффициент корреляции дает объективную оценку тесноты связи лишь при линейной зависимости переменных. Оценка значимости коэффициента корреляции проводится с помощью t – критерия Стьюдента. фактическое значение критерия Если В модель включают те факторы, связь которых с зависимой переменной наиболее сильная. Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т.е. решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных линейно независимы. Для экономических показателей это условие выполняется не всегда. Линейная или близкая к ней связь между двумя факторами называется коллинеарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели.
Считают явление коллинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,7. Чтобы избавиться от коллинеарности, из модели исключают один из линейно связанных между собой факторов. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. С целью выявления факта коллинеарности факторов составляется матрица парных коэффициентов корреляции, измеряющих тесноту связи каждого из факторов – признаков с результативным фактором и между собой (табл. 15).
Таблица 15
Наибольшие трудности при использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности означает, что некоторые факторы будут действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК. Для отображения зависимости переменных могут использоваться показательная, параболическая и многие другие функции. Однако в практической работе наибольшее распространение получили модели линейной взаимосвязи, т.е. когда факторы входят в модель линейно. Линейная модель множественной регрессии имеет вид:
Анализ уравнения и методика определения его параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи этого уравнения: Y – вектор зависимой переменной размерности (nх 1), представляющий собой п наблюдений значений уi; Х – матрица независимых переменных, элементы которой суть п х т наблюдения значений т независимых переменных Х 1, Х 2,..., Хт, размерность матрицы Х равна (п х т); α – подлежащий оцениванию вектор неизвестных параметров размерности (m х 1); ε – вектор случайных отклонений (возмущений) размерности (n х 1). Таким образом,
Величины
где а – вектор оценок параметров; е – вектор «оцененных» отклонений регрессии, е = Y – Ха – остатки регрессии;
Для оценивания неизвестного вектора параметров α. воспользуемся методом наименьших квадратов (МНК). Формула для вычисления параметров регрессионного уравнения имеет вид: В табл. 16 приведены размерности матриц – результатов промежуточных действий. Таблица 16
В случае зависимости переменной Y от одного фактора X имеем
Качество модели оценивается стандартным для математических моделей образом: по адекватности и точности на основе анализа остатков регрессии е. Расчетные значения получаются путем подстановки в модель фактических значений всех включенных факторов. Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности почти независимые), одинаково распределенные случайные величины. В классических методах регрессионного анализа предполагается нормальный закон распределения остатков. Исследование остатков полезно начинать с изучения их графика. Нередко встречаются ситуации, когда остатки содержат тенденцию или подвержены циклическим колебаниям. В этом случае говорят о наличии автокорреляции остатков. Иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения результативного признака. В других случаях автокорреляция указывает на наличие какой–то достаточно сильной зависимости, неучтенной в модели. Существует два наиболее распространенных метода определения автокорреляции остатков. Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод – использование критерия Дарбина – Уотсона и расчет величины
Таким образом, d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии. Коэффициент автокорреляции остатков определятся по формуле
Можно показать, что имеет место соотношение: Если в остатках существует полная положительная автокорреляция и Таким образом, величина d изменяется в пределах: Алгоритм выявления автокорреляции остатков на основе критерия Дарбина – Уотсона следующий. Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы Н1 и Н1* состоят соответственно в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение) определяются критические значения критерия Дарбина – Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели m и уровня значимости
Рис.30. Механизм проверки гипотезы о наличии автокорреляции остатков Если фактическое значение критерия Дарбина – Уотсона попадает в зону неопределенности, то нельзя сделать окончательный вывод по этому критерию. Целесообразно использовать коэффициент множественной корреляции – индекс корреляцииR, а также характеристики существенности модели в целом и отдельных ее коэффициентов: где TSS – общая сумма квадратов отклонений, ESS – сумма квадратов отклонений, объясненная регрессией. Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции. Коэффициент детерминации R2 показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов. В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных. Скорректированный (нормированный) R2, или где n – число наблюдения; m – число независимых переменных. В качестве меры точности модели применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n – m – 1), где m – количество факторов, включенных в модель. Квадратный корень из этой величины называется стандартной ошибкой оценки. Для проверки значимости модели регрессии используется F – критерий Фишера, фактическое значение которого вычисляется как отношение дисперсии исходного ряда и несмещенной дисперсии остаточной компоненты.
Если расчетное значение с k1 = (n – 1) и k2 = (n – m – 1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. Целесообразно проанализировать также значимость отдельных коэффициентов регрессии. Это осуществляется по t – статистике путем проверки гипотезы о равенстве нулю j–го параметра уравнения (кроме свободного члена):
Величина где
Если расчетное значение t-критерия с (n – m – 1) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится). Средние частные коэффициенты эластичности Эj и β –коэффициенты βj, которые рассчитываются соответственно по формулам:
где Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении j–го фактора на 1%. Однако он не учитывает степень колеблемости факторов. Бета–коэффициент показывает, на какую часть величины среднего квадратического отклонения Указанные коэффициенты позволяют ранжировать факторы по степени их влияния на зависимую переменную. Долю влияния фактора в суммарном влиянии всех факторов на результативный признак можно оценить по величине дельта–коэффициентов Δj
где Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Различают точечное и интервальное прогнозирование. В первом случае оценка – это конкретное число, во втором – интервал, в котором истинное значение переменной находится с заданным уровнем доверия. Кроме того, для временных рядов при нахождении прогноза существенно наличие или отсутствие корреляции по времени между ошибками. Для прогнозирования зависимой переменной на l шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены МНК или на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель, и получаются прогнозные оценки. Для линейной модели доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения U от линии регрессии
где Для модели парной регрессии формула принимает вид:
Коэффициент Если исследователь задает вероятность попадания прогнозируемой величины внутрь доверительного интервала, равную 0,7 то Как видно из формулы, величина U прямо пропорционально зависит от точности модели Se, коэффициента доверительной вероятности
В результате получаем следующий интервал прогноза для шага прогнозирования l: • верхняя граница прогноза равна Y(п + l) + U(l), • нижняя граница прогноза равна Y(п + l) – U(l). Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с заданным уровнем значимости можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадет в интервал, образованный нижней и верхней границами.
Постановка задачи: Приводятся данные объема реализации одного из продуктов фирмы (Y). В качестве независимых, объясняющих переменных выбраны следующие временные ряды: Х1 – время, Х2 – расходы на рекламу, Х3 – цена товара, Х4 – средняя цена конкурентов, X5 – индекс потребительских расходов (табл.17). Таблица 17
Требуется: 1. Вычислить матрицу коэффициентов парной корреляции и проанализировать тесноту связи между показателями. 2. Выбрать вид линейной модели регрессии, включив в нее два фактора. Обосновать исключение из модели трех других факторов. 3. Аналитическими методами а) оценить параметры и качество модели, б) вычислить множественный коэффициент детерминации. 4. С целью проверки полученных результатов провести регрессионный анализ выбранной модели с помощью Excel. 5. Проанализировать влияние факторов на зависимую переменную (вычислить соответствующие коэффициенты эластичности и β – коэффициенты, пояснить смысл полученных результатов). 6. По данным прогнозных значений временных рядов, соответствующих оставленным в модели переменным, полученным в лабораторной работе №4, определить точечные и интервальные прогнозные оценки объема реализации продукции фирмы Y на два шага вперед.
Методические рекомендации и выполнение 1. В рассматриваемом примере число наблюдений n = 16, факторных признаков m = 5. Для проведения корреляционного анализа нужно выполнить следующие действия: 1) расположить данные в смежных диапазонах ячеек; 2) выбрать команду Сервис => Анализ данных. Появится диалоговое окно Анализ данных (рис. 31); 3) в диалоговом окне Анализ данных выбрать инструмент Корреляция (рис. 31), щелкнуть по кнопке ОК. появится диалоговое окно Корреляция (рис. 32);
Рис.31. Выбор команды анализ данных 4) в диалоговом окне Корреляция в поле «Входной интервал» необходимо ввести диапазон ячеек, содержащих исходные данные. Если также выделены заголовки столбцов, то установить флажок «Метки в первой строке» (рис.32); 5) выбрать параметры вывода. В данном примере – установить переключатель «Новый рабочий лист»; 6) Щелкнуть по кнопке ОК.
Рис. 32. Диалоговое окно Корреляция На новом рабочем листе получаем результаты вычислений – таблицу значений коэффициентов парной корреляции (рис. 32).
Рис.33. Результаты корреляционного анализа 2. Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем реализации, имеет тесную связь с индексом потребительских расходов: с расходами на рекламу: и со временем: Однако факторы Х 1 и X 5 тесно связаны между собой: что свидетельствует о наличии коллинеарости. Из этих двух переменных оставим в модели X 5 – индекс потребительских расходов. Переменные Х 1 (время), Х 3 (цена товара) и Х 4 (цена конкурента) также исключаем из модели, т.к. связь их с результативным признаком Y (объемом реализации) невысокая. После исключения незначимых факторов имеем n = 16, m = 2. Модель приобретает вид: 3. На основе метода наименьших квадратов проведем оценку параметров регрессии по формуле Таблица 18
Непосредственное вычисление (вычисление «вручную») вектора оценок параметров регрессии а согласно формуле весьма громоздко, т.к. матрица независимых переменных Х имеет довольно высокую размерность (16 х 3), матрица Y – размерности (16 х 1). Задача существенно упрощается при использовании средств Excel. Операции, предписанные формулой (3) целесообразно проводить с помощью следующих встроенных в Excel функций: · МУМНОЖ – умножение матриц, · ТРАНСП – транспонирование матриц, · МОБР – вычисление обратной матрицы. Для вычисления вектора оценок параметров регрессии а в Excel необходимо выполнить следующие действия 1. Ввести данные (табл. 18); 2. Выделить диапазон ячеек для записи вектора а, соответствующий его размерности (3 х 1) (рис. 34); 3. Используя встроенные в Excel функции, ввести формулу, определяющую вектор а; 4. Нажать одновременно клавиши CTRL + SHIFT + ENTER. Появится результат (рис. 35).
Рис.34. Выделяется диапазон ячеек (3 х 1) для записи вектора оценок параметров регрессии а.
Рис.35.Результат вычислений – вектор оценок параметров регрессии а Таким образом, имеем: Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в виде:
Расчетные значения Исследование на наличие автокорреляции остатков проведем с помощью d – критерия Дарбина – Уотсона. Для определения величины d – критерия воспользуемся расчетной таблицей 19. Имеем:
Таблица 19
0 dL d dU 2 4–dU 4– dL 4 Рис. 36. Сравнение расчетного значения d – критерия Дарбина – Уотсона с критическими значениями dL и dU
Так как расчетное значение d – критерия Дарбина–Уотсона попало в зону неопределенности, то нельзя сделать окончательный вывод об автокорреляции остатков по этому критерию. Для определения степени автокорреляции вычислим коэффициент автокорреляции и проверим его значимость при помощи критерия стандартной ошибки. Стандартная ошибка коэффициента корреляции рассчитывается по формуле: Коэффициенты автокорреляции случайных данных должны обладать выборочным распределением, приближающимся к нормальному с нулевым математическим ожиданием и средним квадратическим отклонением, равным
Если коэффициент автокорреляции первого порядка находится в интервале: –1,96 · 0,25 < r 1 < 1,96· 0,25, то можно считать, что данные не показывают наличие автокорреляции первого порядка. Используя расчетную таблицу 19, получаем:
Так как –0,49 < r 1 = 0,3046 < 0,49, то свойство независимости остатков выполняется. Вычислим для построенной модели множественный коэффициент детерминации: = 1 – 22360,1037/158718,4375 = 0,859. множественный коэффициент детерминации показывает долю вариации результативного признака под воздействием включенных в модель факторов Х 2 и Х 5. Таким образом, около 86% вариации зависимой переменной (объема реализации) в построенной модели обусловлено влиянием включенных факторов Х 2 (расходы на рекламу) и Х 5 (индекс потребительских расходов). Проверку значимости уравнения регрессии проведем на основе F – критерия Фишера:
Табличное значение F – критерия при доверительной вероятности 0,95, степенями свободы: k1 = m = 2 и k2 = (n – m – 1) = 16 – 2 – 1 = 13 составляет Fтабл = 3,8. Поскольку Значимость коэффициентов уравнения регрессии а1 и a2 оценим с использованием t – критерия Стьюдента:
Табличное значение t – критерия Стьюдента при уровне значимости 0,05 и степенях свободы 16 – 2 –1 = 13 составляет
то отвергаем гипотезу о незначимости коэффициентов уравнения регрессии а1 и a2. 4. Для проведения регрессионного анализа с помощью Excel выполните следующие действия: 1) выберите команду Сервис => Анализ данных; 2) в диалоговом окне Анализ данных выберите инструмент Регрессия. Щелкните по кнопке ОК; 3) в диалоговом окне Регрессия в поле «Входной интервал Y» введите адрес диапазона ячеек, который представляет зависимую переменную Y. В поле «Входной интервал X» введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (в рассматриваемом примере – переменные Х 2, Х 5). Если выделены заголовки столбцов, то установить флажок «Метки в первой строке»; 5) выберите параметры вывода. В данном примере – установите переключатель «Новая рабочая книга»; 6) в поле «Остатки» поставьте необходимые флажки; 7) Щелкните по кнопке ОК. Результаты представлены на рис. 37 и заключены в таблицах 20 и 21.
Рис.37.Результаты регрессионного анализа, проведенного с помощью Excel
В строках 15-18 таблицы дисперсионного анализа во втором столбце содержатся коэффициенты уравнения регрессии а0, а1, а2, в третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, в четвертом – f – статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
Пояснения к таблице «Регрессионная статистика» Таблица 20
Пояснения к таблице «Дисперсионный анализ» Таблица 21
В строках 20-23 таблицы дисперсионного анализа содержатся доверительные интервалы для результативного признака Y и факторов «Реклама», «Индекс потребительских расходов».
Рис. 38. График остатков В таблице «вывод остатка» (рис. 38) приведены вычисленные по модели значения 5. Проанализируем влияние включенных в модель факторов на зависимую переменную по модели.
Таким образом, при увеличении расходов на рекламу на 1 % величина объема реализации изменится приблизительно на 0,3 %, при увеличении потребительских расходов на 1 % величина объема реализации изменится на 5,5 %.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 933; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.193.129 (0.384 с.) |
 , где
, где ,
, 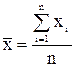 ,
, ,
,  .
. определяется по формуле:
определяется по формуле: 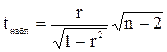 и сравнивается с критическим значением
и сравнивается с критическим значением  , которое берется из таблицы значений t – критерия Стьюдента с учетом заданного уровня значимости (например,
, которое берется из таблицы значений t – критерия Стьюдента с учетом заданного уровня значимости (например,  = 0,05) и числа степеней свободы (n – 2).
= 0,05) и числа степеней свободы (n – 2). , то полученное значение коэффициента корреляции признается значимым, т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается. Таким образом, делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
, то полученное значение коэффициента корреляции признается значимым, т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается. Таким образом, делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.





 .
. , где
, где ,
,  ,
, 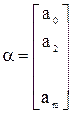
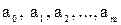 оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид
оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид
 – оценка значений Y, равная Х а.
– оценка значений Y, равная Х а. .
. , где
, где ,
,  .
. .
. , где
, где 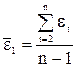 ,
,  .
. .
.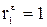 , то
, то  . Если в остатках полная отрицательная автокорреляция и
. Если в остатках полная отрицательная автокорреляция и  , то
, то  .
. .
. 0 dL dU 2 4– dU 4– dL 4
0 dL dU 2 4– dU 4– dL 4 ,
, рассчитывается следующим образом:
рассчитывается следующим образом:  ,
, .
. , где
, где  – стандартное (среднее квадратическое) отклонение коэффициента уравнения регрессии
– стандартное (среднее квадратическое) отклонение коэффициента уравнения регрессии  .
. ,
, – диагональный элемент матрицы
– диагональный элемент матрицы 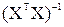 ,
, , где m число факторов, включенных в модель.
, где m число факторов, включенных в модель. ,
,  ,
,
 – среднее квадратическое отклонение фактора j.
– среднее квадратическое отклонение фактора j.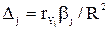 ,
, – коэффициент парной корреляции между j–ым фактором (j = 1,..., m) и зависимой переменной.
– коэффициент парной корреляции между j–ым фактором (j = 1,..., m) и зависимой переменной.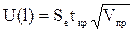 ,
,  ,
, .
. .
.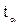 является табличным значением t – статистики Стьюдента при заданном уровне значимости
является табличным значением t – статистики Стьюдента при заданном уровне значимости  , если вероятность составляет 0,95, то
, если вероятность составляет 0,95, то 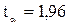 , а при 0,99
, а при 0,99  .
.



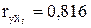 ,
, ,
, .
.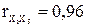 ,
,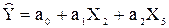 .
.

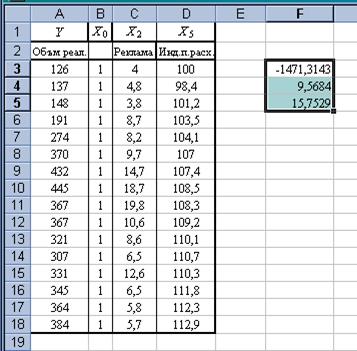
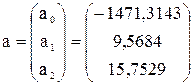 .
. .
. определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого момента времени t.
определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого момента времени t. .
.
 попало в интервал от dL = 0,98 до dU =1,54 (рис. 36)
попало в интервал от dL = 0,98 до dU =1,54 (рис. 36)
 .
. .
. .
.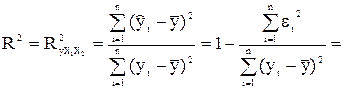
 .
. > Fтабл = 3,8, то уравнение регрессии следует признать адекватным.
> Fтабл = 3,8, то уравнение регрессии следует признать адекватным. ,
, .
.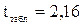 . Так как
. Так как >
>  >
> 



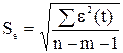







 и значения остаточной компоненты
и значения остаточной компоненты  .
. ,
,  ,
,  ,
,  .
.


