
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества и операции над нимиСтр 1 из 4Следующая ⇒
Множества и операции над ними Основные понятия В основах математического анализа лежит понятие множества. Данное понятие в математике не определено. Под множеством понимают совокупность некоторых объектов, объединенных по какому либо признаку. Объекты, из которых состоит множество, называются его элементами. Множество принято обозначать заглавными буквами латинского алфавита: А, В, Х…, а их элементы – малыми буквами a, b, x. Если элемент принадлежит множеству Х, то пишут § Множество A называется подмножеством множества В, если каждый элемент множества А является элементом множества В (обозначается § Множества, состоящие из одних и тех же элементов, называются равными (обозначается § Объединением множеств А и В (обозначается § Пересечением множеств А и В (обозначается § Разностью множеств А и В (обозначается В дальнейшем при изложении будем использовать следующие символы:
: – «такое что». Числовые множества Одним из основных понятий математики является число. В курсе высшей математики мы будем изучать, в основном, числовые множества. Понятие числа возникло в древности и на протяжении длительного времени подвергалось расширению и обобщению. Первые представления о числе возникли из счета предметов. Результатом счета являются числа 1,2,3,…. Такие числа называются натуральными и обозначаются N. На языке множеств можно записать следующим образом: N ={1,2,3,…}. Натуральные числа, противоположные числа и 0 образуют множество целых чисел: Z ={0,1,-1,2,-2…}. К рациональным числам относят числа вида
Замкнутый интервал (отрезок) Открытый интервал Полуоткрытые интервалы
Полубесконечные интервалы
Бесконечный интервал § Окрестностью точки Далее приведем некоторые понятия, которые будут использоваться нами при изложении. § Абсолютной величиной (или модулем) действительного числа xназывается неотрицательное число Геометрически Приведем без доказательства следующие свойства абсолютной величины: 1) 3) 5) 7) § Переменной величиной называется величина, которая принимает различные численные значения. § Совокупность всех числовых значений переменной величины называется областью изменения этой величины. Функция Некоторые свойства функций ü Функция ü Функция
ü Функцию ü Функцию Обратная функция Пусть задана функция Из определения обратной функции вытекает, что функция Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов. Предел функции Предел функции в точке Пусть функция § Говорят, что функция Кратко это определение записывают, при помощи общепринятых обозначений, перечисленных в п. 8.1., следующим образом:
Геометрически это определение означает, что чем ближе значение аргумента функции х к х 0, тем ближе значение функции у к А (какую бы маленькую мы ни выбрали e-окрестность точки А, найдется такое d, что для всех знасчений аргуимента из d-окрестности точки х 0 значение функции попадет в e-окрестность точки А). Односторонние пределы В определении предела функции § Число А называется пределом функции Бесконечно большие функции § Функция
Иными словами, такая функция f (x) является неограниченной в окрестности точки х 0. Если f (x) – бесконечно большая при
§ Функция
Рис. 19
Здесь
Бесконечно малые функции Основные теоремы о пределах Теорема 11.6. Предел суммы двух функций равен сумме пределов. Доказательство. Пусть Тогда Поскольку сумма двух бесконечно малых функций есть функция бесконечно малая, следовательно
Следствие. Если предел функции существует, то он единственный. Теорема 11.7. Предел произведения двух функций равен произведению пределов, т.е. Теорема 11.8. Теорема 11 9. (Теорема о пределе промежуточной функции.)
Теорема 11.10. Если функция
Техника вычисления пределов. Примеры
Пример 1.
Пример 2.
Пример 3. =
Пример 4.
Пример 5.
Пример 6.
Пример 7. =
Первый замечательный предел Рассмотрим функцию
Так как Разделим данное неравенство на
Следовательно, Итак,
Ниже представлен график функции
Эквивалентные функции § Если Таким образом, поскольку функции Теорема 11.11. Предел отношения двух бесконечно малых не изменится, если каждую или одну из них заменить эквивалентной ей БМФ. Примеры. 1) 2) § Вообще говоря, если 1. если 2. если существует конечный предел 3. если 4. если Говорят, что БМФ одного порядка стремятся к нулю с одинаковой скоростью. Теорема 11.12 Сумма конечного числа БМФ эквивалентна слагаемому низшего порядка. Пример: при § Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы. Замена суммы БМФ ее главной частью называется отбрасыванием БМФ высшего порядка. Теорема 11.13. Разность двух эквивалентных БМФ есть БМФ более высокого порядка. Ниже представлены эквивалентные бесконечно малые, используемые при решении задач на вычисление пределов.
Примеры. 1) 2) 3)
= Второй замечательный предел Вторым замечательным пределом называется предел вида
На графике функции
Данное число является иррациональным, оно названо в честь Леонардо Эйлера, Итак,
Нижеприведенная формула является обобщением второго замечательного предела и используется при вычислениях.
11.7. Техника вычисления пределов вида Пусть
Пример 1. Так как
Пример 2. Так как
Пример 3.
Непрерывность функции Классификация точек разрыва Пусть § Точка
§ Точка
§ Точка
Производная функции Дифференцируемость функций § Если функция
§ Если функция дифференцируема в каждой точке некоторого интервала Теорема 13.1. Если функция (обратное, вообще говоря, неверно). Таким образом, в точках разрыва функция не может иметь производной. Логарифмическая производная Пусть
Пример. Найдем производную функции Прологарифмируем функцию:
Примеры вычисления производных 1) Для вычисления производной сначала преобразуем нашу функцию: Тогда имеем:
2) 3) Воспользуемся формулой производной отношения:
4) Данная функция является сложной, что дает нам право воспользоваться соответствующей формулой. Имеем:
5)
6)
7)
8) Данная функция является неявной. Продифференцируем обе части равенства: 9)
10) Прологарифмируем обе части равенства:
Далее продифференцируем неявную функцию:
Производные высших порядков
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 657; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.203 с.) |
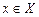 и
и  в случае, если элемент не принадлежит множеству X. Множество, не содержащее ни одного элемента, называется пустым, его обозначают Æ. Множество можно задать либо перечислением его элементов, либо указанием правила по которому элементы объединены в данное множество. Например, множество X ={дедка, бабка, внучка, жучка, кошка, мышка} или X= { x: x – участник сбора урожая репы}.
в случае, если элемент не принадлежит множеству X. Множество, не содержащее ни одного элемента, называется пустым, его обозначают Æ. Множество можно задать либо перечислением его элементов, либо указанием правила по которому элементы объединены в данное множество. Например, множество X ={дедка, бабка, внучка, жучка, кошка, мышка} или X= { x: x – участник сбора урожая репы}. ).
). ).
).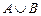 ) называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств. Кратко можно записать следующим образом:
) называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств. Кратко можно записать следующим образом: 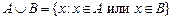 .
. ) называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Кратко:
) называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Кратко:  .
. ) называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и не принадлежит множеству В. Кратко:
) называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и не принадлежит множеству В. Кратко: 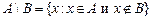 .
. –
–  влечет
влечет  ;
; –
–  – «для всякого», «для любого»;
– «для всякого», «для любого»; – «существует», «найдется»;
– «существует», «найдется»; , где
, где 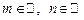 , т.е.
, т.е. 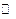 ={
={  содержит все рациональные и иррациональные числа, т.е. является объединением двух множеств. Множество
содержит все рациональные и иррациональные числа, т.е. является объединением двух множеств. Множество  ):
):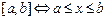 ;
;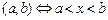 ;
;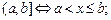



 .
. называется любой интервал (a, b), содержащий точку
называется любой интервал (a, b), содержащий точку 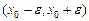 , где
, где  называется
называется 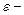 окрестностью точки
окрестностью точки  , определяемое соотношением
, определяемое соотношением 
 выражает расстояние от точки а до точки х. В частности,
выражает расстояние от точки а до точки х. В частности, 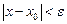 .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; , если | y |¹0.
, если | y |¹0. , определяемая на множестве D является четной, если
, определяемая на множестве D является четной, если  выполняются условия
выполняются условия  и
и  ; нечетной, если
; нечетной, если  . График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
. График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. . Если для любых значений
. Если для любых значений 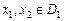 :
:  , то функция называется возрастающей на множестве
, то функция называется возрастающей на множестве  ;
; 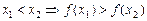 , то функция называется убывающей на множестве
, то функция называется убывающей на множестве  , то функция называется неубывающей на множестве
, то функция называется неубывающей на множестве  , то функция называется невозрастающей на множестве
, то функция называется невозрастающей на множестве 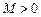 , что для всех
, что для всех  выполняется неравенство
выполняется неравенство 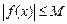 . График ограниченной функции лежит между прямыми
. График ограниченной функции лежит между прямыми  и
и  .
. , что при каждом
, что при каждом  и
и  . Число
. Число  называется периодом функции.
называется периодом функции. соответствует единственное значение
соответствует единственное значение  с областью определения E и множеством значений D. Такая функция
с областью определения E и множеством значений D. Такая функция  и
и  . Тогда всякая строго монотонная функция имеет обратную, при этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
. Тогда всякая строго монотонная функция имеет обратную, при этом если функция возрастает (убывает), то обратная функция также возрастает (убывает). (
( ) при
) при  стремящемся к
стремящемся к 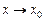 ), если для любого сколь угодно малого
), если для любого сколь угодно малого  , что для всех
, что для всех 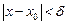 имеет место неравенство
имеет место неравенство 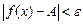 . Записывают следующим образом
. Записывают следующим образом  .
.
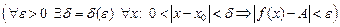 .
. , выполняется неравенство
, выполняется неравенство  или
или  . Аналогично определяется предел функции справа. Обозначается
. Аналогично определяется предел функции справа. Обозначается  или
или  . Пределы функции слева и справа называют односторонними пределами.
. Пределы функции слева и справа называют односторонними пределами. . Записывают:
. Записывают:  .
. ; если такая функция принимает только отрицательные значения, то
; если такая функция принимает только отрицательные значения, то  .
. , если
, если 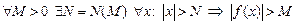 . Записывают:
. Записывают: 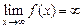 .
. Пример. Рассмотрим функцию
Пример. Рассмотрим функцию  ;
; 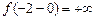 ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 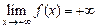 .
. , где
, где  - БМФ. Аналогично, если
- БМФ. Аналогично, если  , то
, то 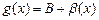 , где
, где  - БМФ.
- БМФ.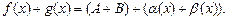
 – бесконечно малая функция. Таким образом, по теореме 5, получим:
– бесконечно малая функция. Таким образом, по теореме 5, получим:



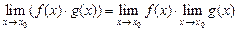 .
. , если
, если  .
. Если функция
Если функция 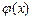 такова, что
такова, что 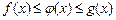 и
и 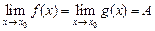 , то
, то 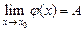 .
. (
( ), то существует
), то существует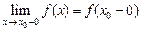 (
( ).
). Для вычисления пределов вида
Для вычисления пределов вида  , где
, где  и
и  многочлены степеней
многочлены степеней 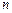 и
и  , необходимо вынести за скобку в числителе
, необходимо вынести за скобку в числителе  и в знаменателе
и в знаменателе  .
.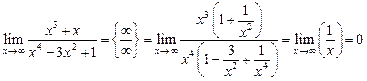 .
. необходимо привести их к пределам вида
необходимо привести их к пределам вида 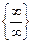 .
.
 . (В данной задаче для преобразования предела к виду
. (В данной задаче для преобразования предела к виду 
 . (В данной задаче для преобразования предела к виду
. (В данной задаче для преобразования предела к виду  необходимо выяснить, определена ли функция при
необходимо выяснить, определена ли функция при 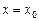 . Если
. Если 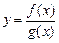 , то
, то  .
.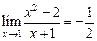 .
. и
и 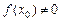 , то
, то 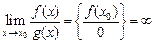 .
.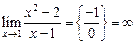 .
.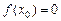 , т.е. если
, т.е. если  , необходимо (в случае
, необходимо (в случае  и
и  ) разделить числитель и знаменатель на
) разделить числитель и знаменатель на 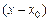 .
.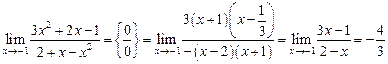 .
.

 .
. . Она не определена при
. Она не определена при  , так как числитель и знаменатель дроби обращаются в нуль. Однако можно заметить, что если
, так как числитель и знаменатель дроби обращаются в нуль. Однако можно заметить, что если 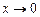 , то значения функций
, то значения функций  и
и  приблизительно одинаковые. Это можно увидеть на представленном ниже рисунке и сравнить значения в таблице.
приблизительно одинаковые. Это можно увидеть на представленном ниже рисунке и сравнить значения в таблице.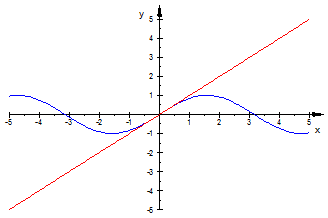
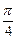

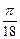

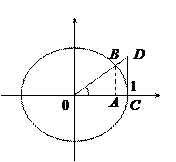 Чем ближе
Чем ближе 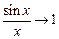 . Итак, докажем формулу
. Итак, докажем формулу 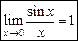 . Для этого рассмотрим единичную окружность. Пусть
. Для этого рассмотрим единичную окружность. Пусть 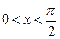 .
.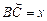 ,
, 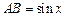 ,
,  .
. , то
, то 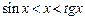 .
. . Знак неравенства при этом не изменится, поскольку
. Знак неравенства при этом не изменится, поскольку  .
. . Воспользуемся теоремой о пределе промежуточной функции. Поскольку при
. Воспользуемся теоремой о пределе промежуточной функции. Поскольку при  и
и  , тогда
, тогда 

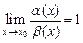 , где
, где  .
. .
.
 . В данном случае заменить невозможно, поскольку функция
. В данном случае заменить невозможно, поскольку функция 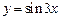 не является бесконечно малой при
не является бесконечно малой при 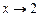 .
.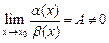 , то
, то  , то
, то  , то
, то  .
.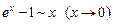
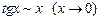





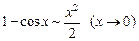

 .
. .
. . Для решения данной задачи сделаем замену переменной. Пусть
. Для решения данной задачи сделаем замену переменной. Пусть  , тогда
, тогда 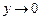 . Имеем:
. Имеем: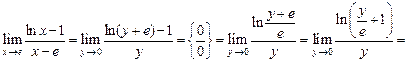
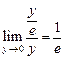 .
. .
.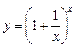 , представленном ниже, видно, что при
, представленном ниже, видно, что при 
 Это число известно читателю как основание натурального логарифма.
Это число известно читателю как основание натурального логарифма.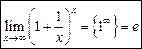 .
.
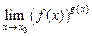 .
. .
. и
и  , то
, то  .
. .
.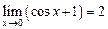 , а
, а 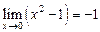 , тогда
, тогда  .
.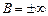 , а
, а  , то
, то

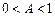


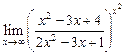 .
.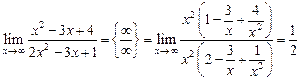 , а
, а 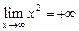 , тогда
, тогда  .
.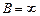 используем формулу
используем формулу
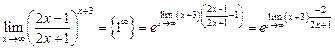 =
=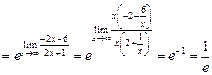 .
. .
.
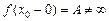 , а
, а  , причем
, причем  .
.
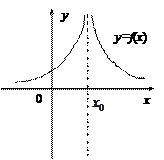

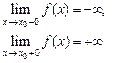
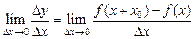 , то мы говорим, что при данном значении
, то мы говорим, что при данном значении 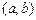 , то она называется дифференцируемой на интервале
, то она называется дифференцируемой на интервале 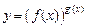 . Прологарифмируем данную функцию. Тогда
. Прологарифмируем данную функцию. Тогда  . Данная функция является неявной. Найдем ее производную:
. Данная функция является неявной. Найдем ее производную: 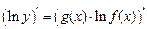
 . Тогда
. Тогда .
. .
. , следовательно,
, следовательно,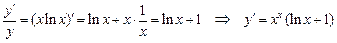 .
.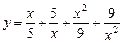 .
. .
.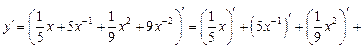
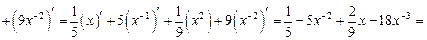
 .
. . Здесь воспользуемся формулой производной произведения. Имеем:
. Здесь воспользуемся формулой производной произведения. Имеем: 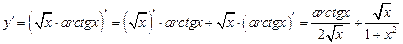 .
. .
.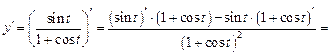
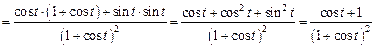
 .
. .
. .
.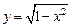 .
.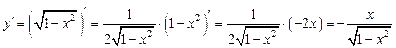 .
. .
.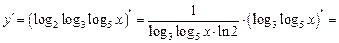

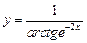 .
.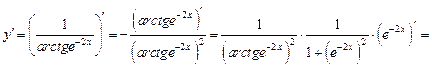
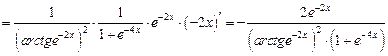 .
. .
.

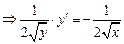
 .
.



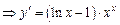 .
.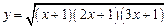 .
.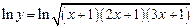
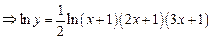
 .
. Þ
Þ Þ
Þ .
.


