
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи линейного программирования.Стр 1 из 3Следующая ⇒
Постановка задачи линейного программирования.
Математическая модель задач поиска наилучшего (экстремального) решения: Целевая функция при ограничениях В зависимости от вида функций
Если целевая функция и функции ограничений являются линейными, то такие задачи относятся к классу задач линейного программирования – ЗЛП. Если или целевая функция и/или функции ограничений являются нелинейными, то такие задачи относятся к классу задач нелинейного программирования – ЗНП. Примеры задач линейного программирования – ЗЛП. Задача об использовании сырья. Для изготовления продукции двух видов П1, П2 требуется сырье видов Запасы сырья ограничены и составляют Требуется: Составить такой план производства продукции двух видов, при котором доход от реализации всей продукции будет максимальным.
Математическая модель задачи 1. Пусть x 1 единиц – объем выпуска продукции П1, x 2 единиц – объем выпуска продукции П2. 2. Цель задачи – максимизировать доход (c 1 x 1+ c 2 x 2) 3. Потребность в сырье s1: (a 11 x 1+ a 12 x 2). Запасы сырья ограничены, поэтому (a 11 x 1+ a 12 x 2) ≤ b 1 . Аналогичные неравенства можно построить для всех видов сырья. Итак, F =(c 1 x 1+ c 2 x 2)→max (a 11 x 1+ a 12 x 2) ≤ b 1 (a 21 x 1+ a 22 x 2) ≤ b 2 (a 31 x 1+ a 32 x 2) ≤ b 3 (a 41 x 1+ a 42 x 2) ≤ b 4 x 1≥0, x 2≥0. Требуется среди всех неотрицательных решений системы линейных ограничений найти такое, при котором линейная форма F достигала бы своего максимального значения.
Задача об использовании мощностей оборудования. Предприятие имеет план производства по времени и номенклатуре: за время Т выпустить N1 ед. продукции вида П1 и N2 ед. продукции вида П2. Продукция каждого вида может производиться на оборудовании А1 и А2, каждое из которых определенной производительности: aij – количество единиц продукции j -го вида, производящейся на i -м оборудовании.
Затраты, связанные с производством продукции вида j на оборудовании вида i составляют cij в ед. времени. Требуется: составить оптимальный план работы оборудования, то есть определить сколько времени должно быть занято оборудование А1 и А2 при производстве П1 и П2 с тем, чтобы затраты на производство всей продукции были бы минимальные при условии выполнения плана по времени и номенклатуре. Математическая модель задачи:
Выполнение плана по номенклатуре для продукта П1:
Итак,
Требуется среди всех неотрицательных решений системы линейных ограничений найти такое, при котором линейная форма F достигала бы своего минимального значения.
Матричная форма основной ЗЛП Заданы:
Целевая функция: 
Система линейных ограничений: Определение 1. Система (2) называется системой линейных ограничений ЗЛП. В системе (2) могут быть ограничения как в виде равенств =, так и в виде неравенств ≥ и ≤. Система (2) не задает условий неотрицательности переменных: x1 ≥0, … Определение 2. Всякое неотрицательное решение Определение 3. Допустимое решение системы (2), минимизирующее линейную форму F, называется оптимальным решением или оптимальным планом. Оптимальное решение может быть единственным, или решений может быть бесконечное множество.
Условия существования оптимального решения ЗЛП. ЗЛП имеет смысл, когда система (2) совместна. Система совместна, если ранги основной и расширенной матриц системы совпадают. Пусть r – ранг, n – число неизвестных. 1. r = n. В этом случае решение единственное, его можно определить поправилу Крамера. 2. r<n. В этом случае, если существует допустимое решение, значит существует и оптимальное (если значение хотя бы одной компоненты вектора решений отрицательно, решение ЗЛП не существует!)
Симплекс-метод
ЗЛП должна быть представлена в основной форме (1) и (2): - Линейная форма - ограничения системы в виде равенств. а) Введем
б) Пусть в системе линейных ограничений имеется неравенство: Введем переменную
Полученное ограничение-равенство эквивалентно ограничению-неравенству, если 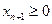 . Т.о. допустимым решением системы (2) будет вектор . Т.о. допустимым решением системы (2) будет вектор  . .
Пример.
n =5; r =3; k =5-3=2. x 1 и x 2 – свободные переменные; x 3, x 4 и x 5 – базисные переменные. Пусть x 1=0 и x 2=0, тогда решением системы будет вектор X =(0,0,12,8, -6). Необходимо увеличить x 5. Это означает, что x 5 необходимо перевести в свободные переменные, а какую-то свободную - x 1 или x 2 в базисные: при x 5 и x 2 – свободные переменные. Выразим
Проанализируем результат Имеем целевую функцию При При Необходимо увеличить x 5. Это означает, что x 5 необходимо перевести в базисные переменные, а какую-то из базисных в свободные.
x 3 и x 2 – свободные переменные.
Увеличиваем x 2
x 3 и x 4 – свободные переменные.
Получили оптимальное решение
Алгебра симплекс-метода (4 часа). Имеется ЗЛП, представленная в форме с ограничениями-равенствами:
Пусть ранг системы  , где k – свободные переменные, , где k – свободные переменные,r – базисные.
Пронумеруем переменные так, чтобы первые k из них были бы свободными, и выразим через них остальные – базисные. Получим: Получили базисное решение, отвечающее выбору свободных неизвестных:
Предположим, что решение – допустимое, то есть  , при этом , при этом  . .
Перейдем от одного допустимого базисного решения к другому допустимому базисному, так чтобы получить уменьшение целевой функции F. Для этого: Представим задачу (3), (4) в виде
Введем обозначения: 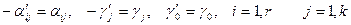 . .
В новых обозначениях
Алгоритм решения
Найти столбцы с положительными коэффициентами
- Составить отношения - Выбрать наименьшее среди этих отношений - Вычислить 3. Величину λ заносим в правый нижний угол i -й строки и j -го столбца. 4. В нижние углы i -й строки записываем произведения 5. В нижние углы j -го столбца записываем произведения
6. Выделяем в i -той строке верхний угол, в j -м столбце – нижний.
7. Заполняем остальные верхний угол i -той строки × нижний угол j-го столбца
8. Строится следующая таблица. Свободная переменная 9. Заполняются i-я строка и j-й столбец: Элементы из нижних углов выделенных строки и столбца переносятся в верхние углы соответствующей клетки.
10. Заполняются верхние углы остальных клеток таблицы: Верхние углы клеток новой таблицы равны алгебраической сумме верхнего и нижнего угла соответствующих клеток предыдущей таблицы.
Таким образом получено новое базисное решение. Решение является оптимальным, если все Все переменные в строке таблицы Базисные переменные – в столбце равны:
Значение целевой функции: 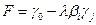
Определение. Основная ЗЛП является невырожденной, если в любом ее допустимом базисном решении, значения всех ее базисных переменных строго положительны. Введем предположения:
(Существует такое с, что при любом допустимом решении, При введенных предположениях справедлива следующая теорема: Теорема. При выполнении предположений (1)-(3) основная ЗЛП имеет, по крайней мере, одно оптимальное базисное решение. Это решение может быть достигнуто симплекс-процессом, исходя из любого допустимого базисного решения за конечное число шагов. Замечания по реализации симплекс-процесса. Рассмотрим 2 случая.
а) в строке F нет положительных коэффициентов. В этом случае получено минимальное значение линейной формы F. б) в F есть
Пример. 
Рекомендация: Сменить столбец или строку, то есть выбрать другой генеральный элемент. Двойственность в ЗЛП Понятие двойственности имеет значение - Теоретического характера. Позволяет анализировать изменение оптимального решения ЗЛП в зависимости от варьирования параметров задачи (Анализ устойчивости решения); - Практического характера. Позволяет осуществлять совершенствование методов планирования и управления. Пример 1. Задача об использовании сырья
Оценим стоимость сырья в зависимости от доходов, которое оно приносит предприятию. Каждый i -й ресурс имеет стоимость - Стоимость используемых ресурсов при производстве единицы j-го продукта будет составлять:
Стоимость используемых ресурсов не может быть меньше дохода - Стоимость ресурсов для производителя должна быть минимальной:
Таким образом, требуется среди всех неотрицательных решений Рассмотренные постановки ЗЛП называются взаимодвойственными.
I. Прямая задача II. Двойственная к ней
Знаки неравенств
Условия задачи max min
Свободные коэффициенты в системе линейных ограничений
Коэффициенты в линейной форме
Правила построения двойственной задачи 1. Если прямая задача имеет целью 2. Каждому ограничению прямой задачи соответствует двойственная переменная, и наоборот. 3. Матрицы ограничений прямой и двойственной задач взаимно транспонированы. 4. Коэффициенты при неизвестных в линейной форме прямой задачи являются свободными членами в ограничениях двойственной, а коэффициенты при неизвестных в линейной форме двойственной задачи являются свободными членами в ограничениях прямой. 5. Каждой неотрицательной переменной прямой задачи соответствует ограничение в виде неравенства в двойственной; переменной, которая может принимать как положительные, так и отрицательные значения, соответствует ограничение типа равенство и наоборот. 6. Перед построением двойственной задачи необходимо привести знаки всех ограничений в соответствие с линейной формой. Если в прямой задаче Если в прямой задаче Теоремы. Постановка задачи линейного программирования.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1012; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.34 (0.152 с.) |


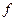 и
и  задачи поиска наилучшего (экстремального) решения относятся к различным классам.
задачи поиска наилучшего (экстремального) решения относятся к различным классам. .
.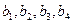 усл. ед. Известно aij – количество сырья вида i для изготовления продукции П j, i =1,4, j =1,2. Доход предприятия от реализации единицы продукции П j составит cj ден. ед.
усл. ед. Известно aij – количество сырья вида i для изготовления продукции П j, i =1,4, j =1,2. Доход предприятия от реализации единицы продукции П j составит cj ден. ед.

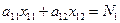


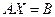
 системы (2) называется допустимым решением или планом ЗЛП.
системы (2) называется допустимым решением или планом ЗЛП.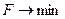
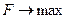 .
.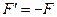 . Тогда
. Тогда  . При этом вектор решений ЗЛП не изменится.
. При этом вектор решений ЗЛП не изменится.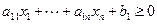
 , связанную с вектором переменных ЗЛП
, связанную с вектором переменных ЗЛП  уравнением
уравнением
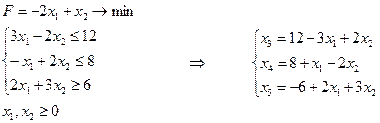
 , при
, при  .
.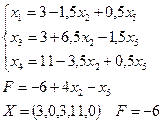
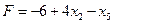
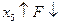 .
.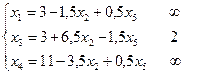

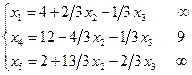


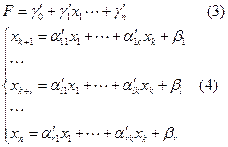


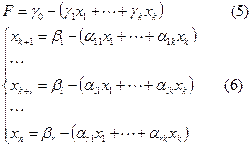
 . При этом
. При этом 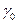 не учитывается. Пусть это будет
не учитывается. Пусть это будет  . Если все
. Если все 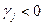 , то базисное решение будет оптимальным.
, то базисное решение будет оптимальным. ;
; ;
;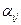 - генеральный элемент и
- генеральный элемент и  .
. .
. .
. клетки симплекс-таблицы. В нижний угол заносится произведение:
клетки симплекс-таблицы. В нижний угол заносится произведение: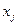 меняется местами в таблице с базисной переменной
меняется местами в таблице с базисной переменной 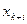 .
.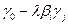
 xk+1
xk+1
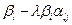 …
…
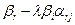

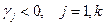 . Если хотя бы один коэффициент при неизвестных в целевой функции F положительный, преобразование симплекс-таблицы продолжается, начиная с п. 2.
. Если хотя бы один коэффициент при неизвестных в целевой функции F положительный, преобразование симплекс-таблицы продолжается, начиная с п. 2. являются свободными и равны 0.
являются свободными и равны 0.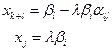
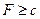 .)
.) , но в выбранном столбце для поиска генерального элемента нет положительных коэффициентов
, но в выбранном столбце для поиска генерального элемента нет положительных коэффициентов  . Это означает, что F не ограничена снизу. То есть, при
. Это означает, что F не ограничена снизу. То есть, при 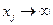 все базисные переменные останутся положительными.
все базисные переменные останутся положительными.
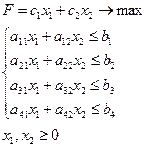
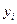 .
.
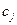 .
.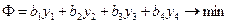
 достигала бы своего минимума.
достигала бы своего минимума.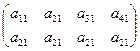 Матрицы коэффициентов
Матрицы коэффициентов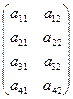
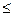
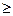
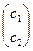
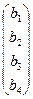
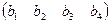
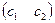
 , то двойственная имеет целью
, то двойственная имеет целью 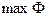 , и наоборот.
, и наоборот.


