
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двоїсті задачі та їх рішення
Кожній задачі лінійного програмування ставлять у відповідність іншу задачу, побудовану на основі тих же даних за визначеними правилами. Ці правила зводяться до наступного: § всі обмеження вихідної задачі приводять до одного виду: у випадку § виписують матрицю коефіцієнтів при невідомих § використовують нові змінні (невід’ємні) і на основі транспонованої матриці формують обмеження двоїстої задачі. Знак нерівностей беруть протилежним стосовно знака нерівностей вихідної задачі. Для правої частини обмежень використовують коефіцієнти цільової функції вихідної задачі; § складають цільову функцію двоїстої задачі, беручи для коефіцієнтів праві частини обмежень вихідної задачі. Спрямованість цільової функції двоїстої задачі буде протилежна спрямованості цільової функції вихідної задачі. Наприклад, для задачі, вирішеної симплексним методом, складемо двоїсту, виходячи з приведених правил.
Перехід від будь-якої задачі до двоїстої можна виконати, використовуючи табличну схему:
Запис однієї задачі йде по рядках, іншої – по стовпцях.
! Необхідно запам’ятати, що при рішенні однієї з двох двоїстих задач автоматично вирішується і друга, і значення цільових функцій у них співпадають. Рішення двоїстої задачі зі зворотним знаком міститься в Наприклад, у розглянутій задачі мали:
Додатковими були стовпці
Розгляд двоїстих задач дуже корисно, тому що вони мають самостійний економічний зміст і дозволяють вивчати економічний процес з різних сторін. Аналіз матричної гри Теорія ігор – це математична теорія конфліктних ситуацій. Гра – конфліктна ситуація, регламентована визначеними правилами: § порядок виконання ходів; § порядок виконання кожного ходу; § кількісний результат гри. Найбільш вивчені матричні ігри. Наприклад,
У цій грі два учасники – сторона
Вирішити гру – значить, дати рекомендації кожній зі сторін щодо використання їхніх стратегій. Попередньо гру аналізують за “принципом міні-максу”. Він полягає у виборі найбільш обережної стратегії, виходячи з найгіршого способу дії іншої сторони. а) Аналізуємо гру з позицій сторони б) Аналізуємо гру з позиції сторони в) Ціна гри Якщо
де
Кожній матричній грі можна поставити у відповідність дві двоїсті задачі лінійного програмування, які відображають інтереси сторін. Для сторони
Аналіз матричної гри проводиться в два етапи: § формулюються двоїсті задачі, вирішують одну з них симплекс-методом і записують рішення обох двоїстих задач; § визначають рішення гри. 1. Запишемо дві двоїсті задачі на основі приведеної платіжної матриці:
Симплексне рішення зручно проводити для першої задачі, тому що в ній не буде штучних змінних. Дана задача приймає вигляд:
У результаті використання симплекс-алгоритму одержимо:
Рішення буде мати вигляд: а)
б)
2. Знайдемо рішення гри: а) визначимо ціну гри, – ця величина характеризує кількісний результат гри:
б) знайдемо ймовірності стратегій:
в) складемо оптимальні стратегії для учасників
Як бачимо, для досягнення оптимального результату стороні
Метод потенціалів Цей метод використовується для рішення багатьох розподільних задач, що містять велике число змінних і відповідають вимозі цілочисельності рішення. Такими, зокрема, є транспортні задачі, на них і буде проілюстрований алгоритм методу. Теоретичні основи методу такі: § необхідною і достатньою умовою існування рішення є баланс між попитом та пропозицією; § по завантажених клітинках визначають систему потенціалів:
де
§ в оптимальному розподілі сума потенціалів рядка і стовпця не повинна перевершувати тариф відповідної незавантаженої клітинки; § кількість постачань повинна дорівнювати величині Метод потенціалів здійснюється в три етапи: 1. Побудова первісного опорного плану (початковий розподіл вантажів). 2. Оцінка оптимальності розподілу вантажів за допомогою системи потенціалів. 3. Поліпшення плану перевезень, якщо воно можливо. Другий і третій етапи повторюються доти, поки рішення не стане оптимальним.
I етап. Побудова початкового опорного плану Початковий розподіл можна виконувати різними способами: способом північно-західного кута, способом найменших тарифів, подвійної переваги, способом Фогеля, способом Лебедєва-Тихомирова й ін. Найбільш простим і легко реалізованим на ЕОМ є спосіб північно-західного кута. Він полягає в тім, що від кожного постачальника, починаючи з першого, вивозять весь вантаж з урахуванням потреби споживачів. Розподіл завершено, якщо весь вантаж від постачальників вивезений, а кожен споживач одержав необхідний обсяг.
Розглянемо приклад: є три постачальники Таблиця 1
Установимо, насамперед, наявність балансу між попитом та пропозицією 250 + 150 + 250 = 650 200 + 250 + 200 = 650 Баланс є. Тепер розподілимо вантаж, починаючи з першої верхньої клітинки, звідси і назва способу – північно-західний кут. Розподіл завершено, необхідно визначити витрати (величину
II етап. Оцінка оптимальності рішення По завантажених клітинках складемо систему рівнянь для потенціалів, попередньо перевіривши кількість заповнених кліток. Їх повинно бути
Маємо систему з 5 рівнянь з 6 невідомими, тому один з потенціалів приймемо рівним 0. Частіше за все беруть
Тепер необхідно перевірити виконання другої умови оптимальності рішення: сума потенціалів для незаповненої клітинки не повинна перевищувати величину тарифу в ній.
Умова оптимальності для жодної з порожніх клітинок не виконується. Варто поліпшити рішення.
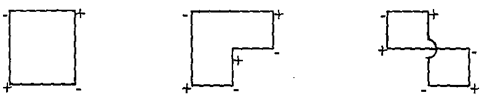
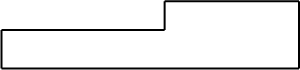
III етап. Побудова нового розподілу З усіх клітинок, для яких умова оптимальності не виконується, вибирають ту, у якій розбіжність найбільша. Якщо таких клітинок декілька, то вибирають клітину з меншим тарифом. Її позначають знаком “+”. Починаючи від обраної клітинки, будують прямокутну фігуру, всі інші вершини якої розташовуються в заповнених клітинках. Знаки вершин чергують. Прямокутні фігури можуть бути наступних видів:
Рідше зустрічаються фігури такого виду:
Вид фігури зумовлюється розподілом постачань. З усіх клітинок, відзначених знаком мінус, вибирають найменший вантаж. Його переміщують уздовж прямокутної фігури, додаючи, якщо стоїть знак “+”, і, віднімаючи, якщо стоїть знак “–”. Усі зміни відображають у новій таблиці. Величини, що не беруть участь у перерозподілі, у нову таблицю переносять без зміни. Звернемося до приклада: у таблиці 1 знаком “–” відзначені дві клітинки, вибираємо найменший вантаж 50 і переміщуємо його уздовж прямокутної фігури. Усі зміни показані у табл. 2. Отримано новий розподіл: необхідно оцінити його, тому повертаємося до II етапу алгоритму.
Таблиця 2
Перевіримо число заповнених клітинок, їх як і раніше 5. Знову знаходимо потенціали, причому можна не складати систему, а використовувати правила: 1. У 1 рядку беремо 0. 2. Невідомий потенціал стовпця дорівнює різниці між тарифом заповненої клітинки і відомим потенціалом рядка. 3. Невідомий потенціал рядка дорівнює різниці між тарифом заповненої клітинки і відомим потенціалом стовпця. Чергуючи ці правила, знайдемо потенціали. Перевірку оптимальності також можна проводити безпосередньо в таблиці, ставлячи “точку”, якщо умова виконується, і, вказуючи в круглих дужках величину розбіжності у випадку невиконання умови. У нашому прикладі найбільша розбіжність між сумою потенціалів і тарифами – у клітинці (2; 1). Будуємо прямокутну фігуру і зауважуємо, що дві клітинки, відзначені знаком “–”, мають однакову найменшу величину 150, – цей факт веде до виродженого розподілу. І дійсно, після переміщення одержимо таблицю 3, у якій число завантажених клітинок дорівнює 4. Таблиця 3
Виродженість може з’явитися і зникнути при переході від таблиці до таблиці. Щоб продовжити рішення у випадку виродженої задачі, вводять нульові постачання, відповідні клітинки вважають умовно заповненими. Нулів буде стільки, скільки бракує постачань. Їх вписують у клітинки, що мають малі витрати, і при цьому стежать, щоб не виходив замкнутий цикл (прямокутна фігура, у всіх вершинах якої – заповнені клітинки). У даному прикладі варто вписати один нуль і найкраще в клітинку (3; 1). Подальше рішення звичайне: знаходять потенціали, перевіряють умову оптимальності. Після чергового перерозподілу одержимо таблицю 4. Таблиця 4
Задача знову стала невиродженою – число завантажених клітинок дорівнює 5. Умова оптимальності виконується. Розміщення вантажів видно з таблиці. Знайдені суми витрат на кожнім етапі рішення:
Зауваження 1. Якщо ми маємо справу з відкритою транспортною задачею, то для її рішення необхідно спочатку забезпечити баланс між попитом та пропозицією. Для цього вводять додаткового постачальника, якщо попит перевищує пропозицію, у противному випадку вводять додаткового споживача. Якщо додають постачальника, то його “потужністю” буде величина, яку бракує до балансу, транспортні тарифи беруть рівними нулю. Аналогічно діють, якщо додають споживача. Надалі рішення проводять по викладеному вище алгоритму. Уведення додаткового постачальника або споживача має цілком визначене економічне пояснення. У першому випадку ми визначаємо, якому споживачу вигідніше недопоставити вантаж, виходячи з інтересів всіх учасників, у другому випадку – у якого постачальника доцільніше за все залишити частину вантажу. Зауваження 2. Раніше був докладно розглянутий спосіб північно-західного кута для початкового розподілу вантажів. Число ітерацій (таблиць) можна зменшити, якщо скористатися способом найменших тарифів. Він полягає в аналізі всієї матриці тарифів, виборі найменших значень і максимальному заповненні відповідних клітинок таблиці. Ці дії виконуються доти, поки не буде розподілений весь вантаж і вдоволений попит усіх споживачів. У результаті заповнення однієї з клітинок виключається з розгляду якийсь постачальник або споживач. При цьому додаткові учасники транспортної задачі приймаються до уваги в останню чергу. Розглянемо приклад транспортної задачі.
Балансу між попитом та пропозицією нема, необхідно ввести додаткового постачальника з потужністю 150 тис. одиниць. Розподіл виконаємо способом найменших тарифів
Отриманий план не оптимальний, варто перейти до кращого. Це можна зробити на основі викладеного алгоритму.
Задачі про призначення
Проблема, яка полягає в тому, щоб правильно розподілити наявні людські ресурси відповідно до професійних вимог, актуальна в різних сферах – в армії, у промисловості, у кадровій політиці будь-якої структури. Математичне програмування є одним з важливих інструментів в області раціонального використання персоналу. Центральне місце в зазначеній проблемі займає задача про призначення. У ній змінні інтерпретуються як призначення відповідної людини на визначену роботу. Кожна змінна може приймати лише значення, які дорівнюють одиниці (претендент обраний) чи нулю (претендент не обраний). Математична структура цієї задачі така:
де Наприклад, якщо § приходиться вносити в таблицю значну кількість нулів, що викликає деякі утруднення; § прямокутна фігура перерозподілу величин частіше за все буває досить складною. Приклад. Сім претендентів розподіляються на 7 ділянок діяльності. Розв’язується задача на мінімум витрат. Послідовність використання претендентів і перерозподіли відображені в таблицях 1 – 3. Таблиця 1
Навчальний розподіл був виконаний по методу найменших тарифів. Таблиця 2
В таблиці 2 розподіл потребує поліпшення. Таблиця 3
У таблиці 3 умова оптимальності виконується, конкретні призначення помітні. Якщо розглядається задача на максимум ефективності використання персоналу, то крім зазначених особливостей істотно міняється алгоритм методу потенціалів: § розподіл варто вести за найбільшими показниками ефективності; § розташовувати нулі також треба в клітинки з великими тарифами; § умова оптимальності протилежна традиційній – сума потенціалів для порожніх клітинок повинна бути не менше тарифу, саме в цьому випадку буде досягнутий максимум. Приклад. Розглянемо ту ж саму матрицю тарифів, припускаючи, що в ній зазначені показники ефективності. Таблиця 1
Таблиця 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.111.125 (0.132 с.) |
 обмеження повинні мати вид нерівностей типу “
обмеження повинні мати вид нерівностей типу “ 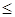 ”, у випадку
”, у випадку  - типу “
- типу “  ”. Нерівності, що не відповідають цій умові, множать на (- 1);
”. Нерівності, що не відповідають цій умові, множать на (- 1); і транспонують її
і транспонують її  ;
;

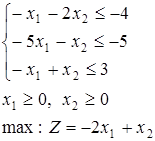

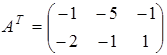






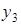



 -рядку останньої симплексної таблиці в додаткових стовпцях.
-рядку останньої симплексної таблиці в додаткових стовпцях.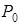
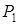
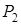
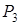
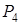

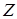 -рядок
-рядок
 .
.






 і сторона
і сторона 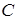 , у кожного учасника по 3 стратегії. Будемо уважати, що матриця характеризує виграш сторони
, у кожного учасника по 3 стратегії. Будемо уважати, що матриця характеризує виграш сторони 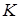 . Якщо гравець вибирає стратегію
. Якщо гравець вибирає стратегію  .
. . Якщо гравець вибирає стратегію
. Якщо гравець вибирає стратегію  .
. – це величина, що відображає об’єктивне співвідношення сил, вона завжди задовольняє умові:
– це величина, що відображає об’єктивне співвідношення сил, вона завжди задовольняє умові: 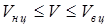 . У даному прикладі:
. У даному прикладі:  .
. , то гра має рішення в конкретних стратегіях, що називаються оптимальними. Ці оптимальні стратегії є стійкими, забезпечують рівновагу в грі, а ціна гри називається “ сідловою точкою ”. Якщо такої ситуації нема, то оптимальні стратегії будуть виглядати так:
, то гра має рішення в конкретних стратегіях, що називаються оптимальними. Ці оптимальні стратегії є стійкими, забезпечують рівновагу в грі, а ціна гри називається “ сідловою точкою ”. Якщо такої ситуації нема, то оптимальні стратегії будуть виглядати так: ;
;  .
. – ймовірності стратегій сторони
– ймовірності стратегій сторони  – ймовірності стратегій сторони
– ймовірності стратегій сторони 

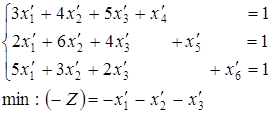
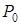

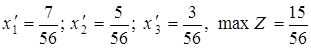

 .
. ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. ;
; 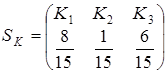 .
. використовувати 3 рази, стратегію
використовувати 3 рази, стратегію  – 5 разів, стратегію
– 5 разів, стратегію  – найчастіше, а саме 7 разів. Для сторони
– найчастіше, а саме 7 разів. Для сторони 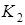 – рекомендується використовувати рідше всього – 1 раз з 15, набагато частіше потрібно застосовувати стратегію
– рекомендується використовувати рідше всього – 1 раз з 15, набагато частіше потрібно застосовувати стратегію 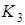 – 6 разів з 15, і найбільше – стратегію
– 6 разів з 15, і найбільше – стратегію 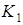 . Якщо хтось з учасників відхилиться від цих рекомендацій, то він погіршить тільки своє власне становище.
. Якщо хтось з учасників відхилиться від цих рекомендацій, то він погіршить тільки своє власне становище. ,
,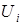 – потенціал рядка;
– потенціал рядка; – потенціал стовпця;
– потенціал стовпця;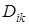 – тариф відповідної клітинки.
– тариф відповідної клітинки. , де
, де  - число постачальників,
- число постачальників,  - число споживачів.
- число споживачів. і три споживачі
і три споживачі  , відомі потужності постачальників, попит споживачів і тарифи на перевіз вантажу (табл. 1).
, відомі потужності постачальників, попит споживачів і тарифи на перевіз вантажу (табл. 1).



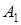
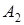

 .
. . Саме стільки і є. Сума потенціалів рядка і стовпця повинна дорівнювати транспортним тарифам завантажених клітинок; на основі чого одержуємо систему для потенціалів:
. Саме стільки і є. Сума потенціалів рядка і стовпця повинна дорівнювати транспортним тарифам завантажених клітинок; на основі чого одержуємо систему для потенціалів: ;
;  ;
;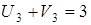 ;
;  ;
;  .
. і знаходять всі інші потенціали:
і знаходять всі інші потенціали: ;
;  ;
;  ;
;  ;
;  .
.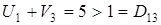 ;
;  ;
; ;
;  .
.


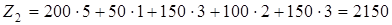 .
.
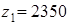 ,
,  ,
,  ,
,  . На кожнім етапі одержували рішення краще попереднього.
. На кожнім етапі одержували рішення краще попереднього.
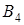
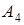

 ,
, 
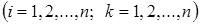
 чи
чи 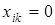 ,
, – показники витрат (чи ефективності)
– показники витрат (чи ефективності)
 1
1

 . Це розміщення виявилося не оптимальним, що привело до необхідності покращення рішення, тобто до перерозподілу претендентів.
. Це розміщення виявилося не оптимальним, що привело до необхідності покращення рішення, тобто до перерозподілу претендентів. .
. .
. 1
1
 1
1



